手把手教做无人驾驶算法（二十六）--基于终端约束的MPC 控制

最新推荐文章于 2025-09-23 00:22:44 发布

原创

最新推荐文章于 2025-09-23 00:22:44 发布 · 6.3k 阅读

29 ·

CC 4.0 BY-SA版权

文章标签：

#自动驾驶 #算法

本文介绍了基于终端约束的模型预测控制（MPC）在稳定性与可行性方面的分析。通过数据驱动的方法，终端约束可以增强MPC的性能，不仅与数据驱动结合，还能扩大可行域。文章提供了计算安全集和终端约束的代码示例，并对比了有无终端约束的轨迹效果，强调了终端约束在控制策略中的重要性。

关于MPC终端约束问题，其实就是稳定性与可行性的分析，欢迎感兴趣的一起交流探讨，如有错误，还请指正，不胜感激。

基于终端约束的MPC控制，理论部分可以参考资料：

【Linear MPC入门】Model Predictive Control Algorithm, Feasibility and Stability - 知乎

这里，终端约束数据可以用数据驱动来代替，这样就可以把MPC与数据驱动相结合起来，但是好处不仅仅是为了与数据驱动联合，终端约束有什么好处呢？上面的参考资料也给出了参考。

对于一般MPC而言，相当于零点为终点，不过，使用Zero Terminal Constraint是非常苛刻的，导致可行域减少了很多。同时，MPC的预测的步数N越少，可行域也越少。

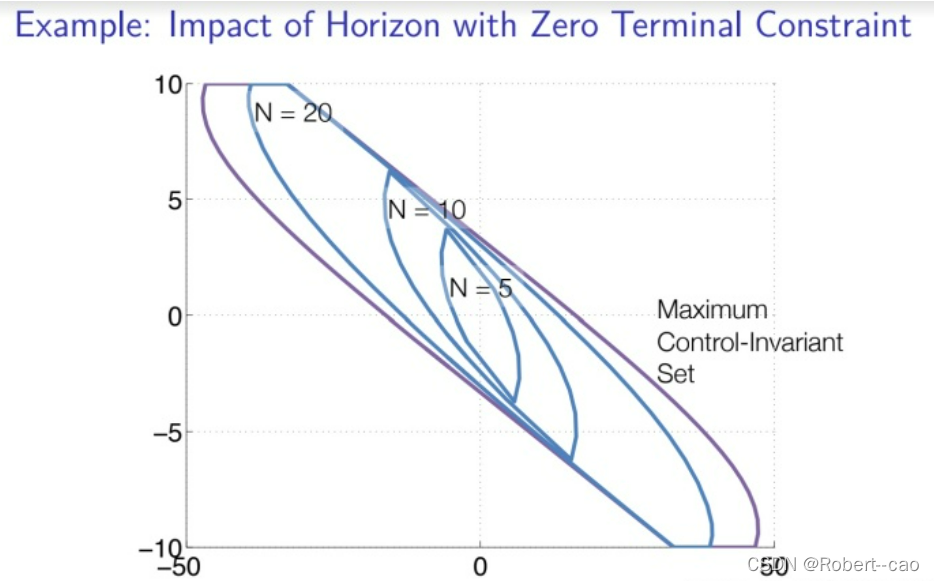
对于可行域使用凸多面体表示，如上图：

function [ invariantGoalSet ] = computeInvariantGoalSet( A, B, Q, R )

[K,~,~] = dlqr(A,B,Q,R);

Acl = A-B*K;
w_max = 0.05;
W = Polyhedron([w_max w_max; w_max -w_max; -w_max -w_max; -w_max w_max]);

X{1} = zeros(size(Acl,1),1); % Initialize the set
for i = 1:10000
    Set = Acl*X{i} + W; % Propagate