【自适应互补滤波MATLAB例程】基于幅值自适应的互补滤波方法与标准互补滤波对比，MATLAB例程，附下载链接

最新推荐文章于 2026-01-07 22:33:13 发布

原创最新推荐文章于 2026-01-07 22:33:13 发布 · 714 阅读

24 ·

CC 4.0 BY-SA版权

文章标签：

#matlab #开发语言 #互补滤波 #自适应滤波 #滤波

在这里插入图片描述

标准互补滤波与基于幅值自适应机制的改进互补滤波的对比仿真，用于分析两种方法在存在噪声、漂移与外加加速度干扰情况下的姿态角估计性能差异。

文章目录

程序介绍
仿真背景与目的
算法原理
仿真设计

运行结果
MATLAB源代码

程序介绍

程序实现标准互补滤波器与基于幅值自适应机制的改进互补滤波器的对比仿真，用于分析两种方法在存在噪声、漂移与外加加速度干扰情况下的姿态角估计性能差异。

仿真背景与目的

在姿态估计中，陀螺仪提供角速度信息，通过积分可获得角度，但容易累积漂移误差；加速度计可直接估计角度，但对动态加速度极其敏感。
传统互补滤波通过固定权重 $\alpha$ 融合两者，实现对高频和低频误差的互补抑制，但当运动状态变化剧烈或噪声波动较大时，固定参数会导致滤波性能下降。
为此，本文提出一种基于新息幅值的自适应互补滤波算法，能根据实时观测残差（新息）的大小自动调整权重系数，使滤波器在稳定与剧烈运动时都能保持较优性能。

算法原理

标准互补滤波器
幅值自适应互补滤波
引入新息幅值 $|\theta_{acc} - \theta_{gyro}|$ 反映传感器差异，根据其大小动态调整权重，并通过平滑更新，实现幅值自适应调节机制，在外界干扰较大时减小对加速度计的信任，在系统稳定时增大融合比例，从而提高整体鲁棒性。

仿真设计

仿真角度设为正弦运动；
陀螺仪含随机噪声与漂移项；
加速度计在 3~6 秒 引入外部加速度干扰；
采用 0.01 s 采样时间进行 10 s 的模拟。

程序绘制了以下对比结果：

原始传感器数据曲线： 显示加速度计、陀螺仪与真实角度的差异；
角度估计曲线： 比较标准互补滤波与自适应互补滤波的估计结果；
误差时域曲线： 展示各方法在时间域的估计误差；
RMSE统计柱状图： 量化不同算法的均方根误差。

结果表明：

标准互补滤波能有效抑制漂移，但在加速度干扰时存在明显偏差；
幅值自适应互补滤波能根据实时新息自动调整融合比例，使误差在整个过程中保持较小波动；
在 RMSE 对比中，自适应滤波的整体精度显著优于标准互补滤波。

运行结果

滤波前后的角度对比：
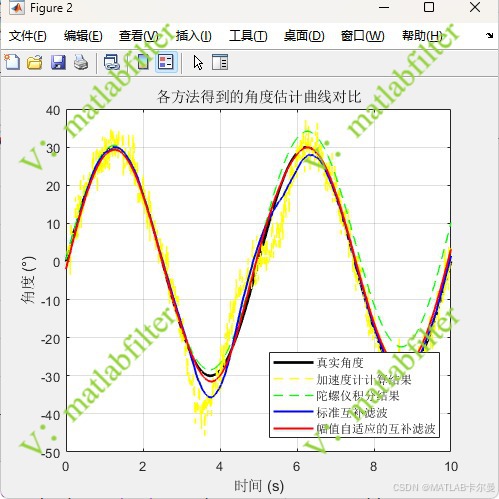
在这里插入图片描述
滤波前后的角度误差对比：

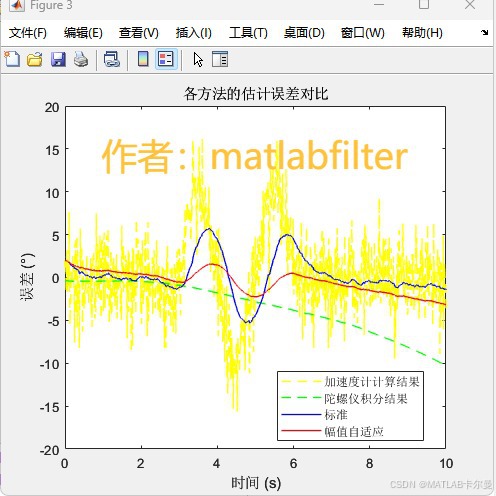
RMSE对比：

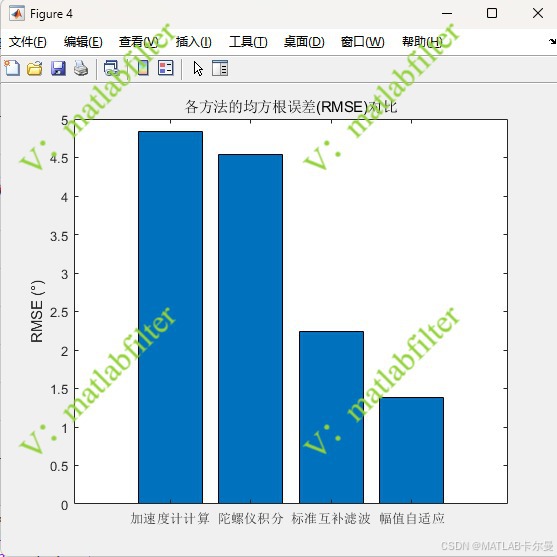
在这里插入图片描述

MATLAB源代码

部分代码如下：

%% 基于幅值自适应的互补滤波器方法与标准互补滤波对比
% 作者：matlabfilter
% 2025-10-27/Ver1

clear; close all; clc;
rng(0);
%% 生成仿真数据
dt = 0.01; % 采样时间
t = 0:dt:10; % 时间向量
N = length(t);

% 真实角度 (正弦运动)
true_angle = 30*sin(2*pi*0.2*t);
true_angular_vel = 30*2*pi*0.2*cos(2*pi*0.2*t);

% 陀螺仪数据 (带漂移和噪声)
gyro_noise = 0.5; % 陀螺仪噪声标准差
gyro_drift = 0.2*t; % 陀螺仪漂移
gyro_data = true_angular_vel + gyro_drift + gyro_noise*randn(1,N);

% 加速度计数据 (带噪声和外部加速度干扰)