【IMM&CKF】基于容积卡尔曼滤波（CKF）的多模型交互的定位程序，模型为CV和CT，三维环境，matlab代码|附下载链接

程序的核心是使用容积卡尔曼滤波（CKF）处理非线性观测问题，并集成匀速（CV）和匀角速度转弯（CT）两种运动模型，通过模型交互提高定位精度。同时，程序还包含单模型CKF（纯CV和纯CT）的对比分析，便于评估IMM方法的性能优势。

程序简介

以下是对程序关键部分的概述：

1. 程序目的与核心算法

   • 目标：模拟三维空间中机动目标的轨迹跟踪，例如无人机或飞行器，在存在过程噪声和观测噪声的情况下，估计目标的位置和速度状态。
   • 核心滤波方法：容积卡尔曼滤波（CKF）用于处理非线性观测模型（球坐标到笛卡尔坐标的转换）。CKF通过容积点近似非线性函数，避免雅可比矩阵计算，提高数值稳定性。
   • 模型交互：采用交互多模型（IMM）框架，动态切换CV和CT模型。IMM包括模型概率计算、混合初始条件和模型特定滤波步骤，以处理目标机动（如直线运动到转弯运动）。

2. 运动模型描述

   • CV模型（匀速模型）
     过程噪声协方差矩阵 $Q_{\text{cv}}$ 基于噪声强度 $q_{\text{cv}}$ 和采样时间 $T$ 构建。
   • CT模型（匀角速度转弯模型）

更多参数信息详见代码注释或专栏文章：

• 【IMM&CKF】基于容积卡尔曼滤波（CKF）的多模型交互的定位程序，模型为CV和CT，三维环境，matlab代码，订阅专栏后可查看完整代码：https://blog.youkuaiyun.com/callmeup/article/details/149329717?spm=1011.2415.3001.5331

单独的下载链接：

• IMM&CKF基于容积卡尔曼滤波（CKF）的多模型交互的定位程序，模型为CV和CT，三维环境，matlab代码

运行结果

三维轨迹图如下，含各方法估计的轨迹对比：

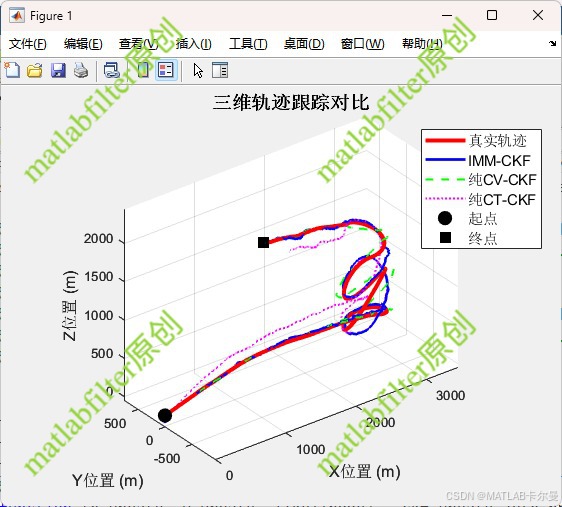
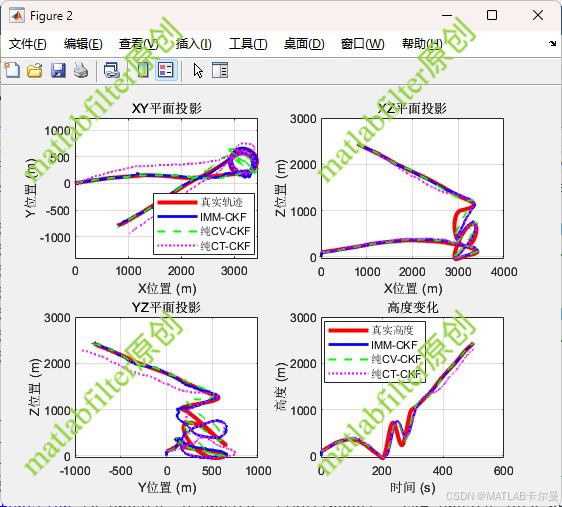
三轴误差曲线，如下：

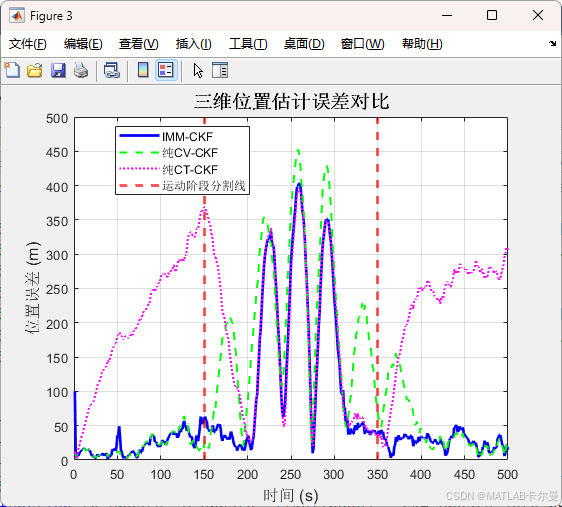
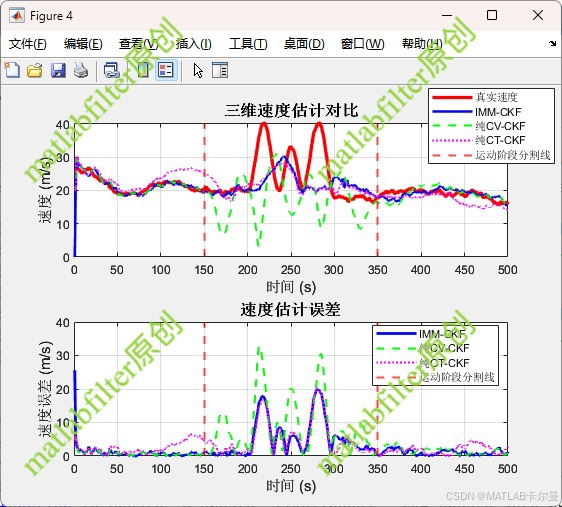
定位结果输出：

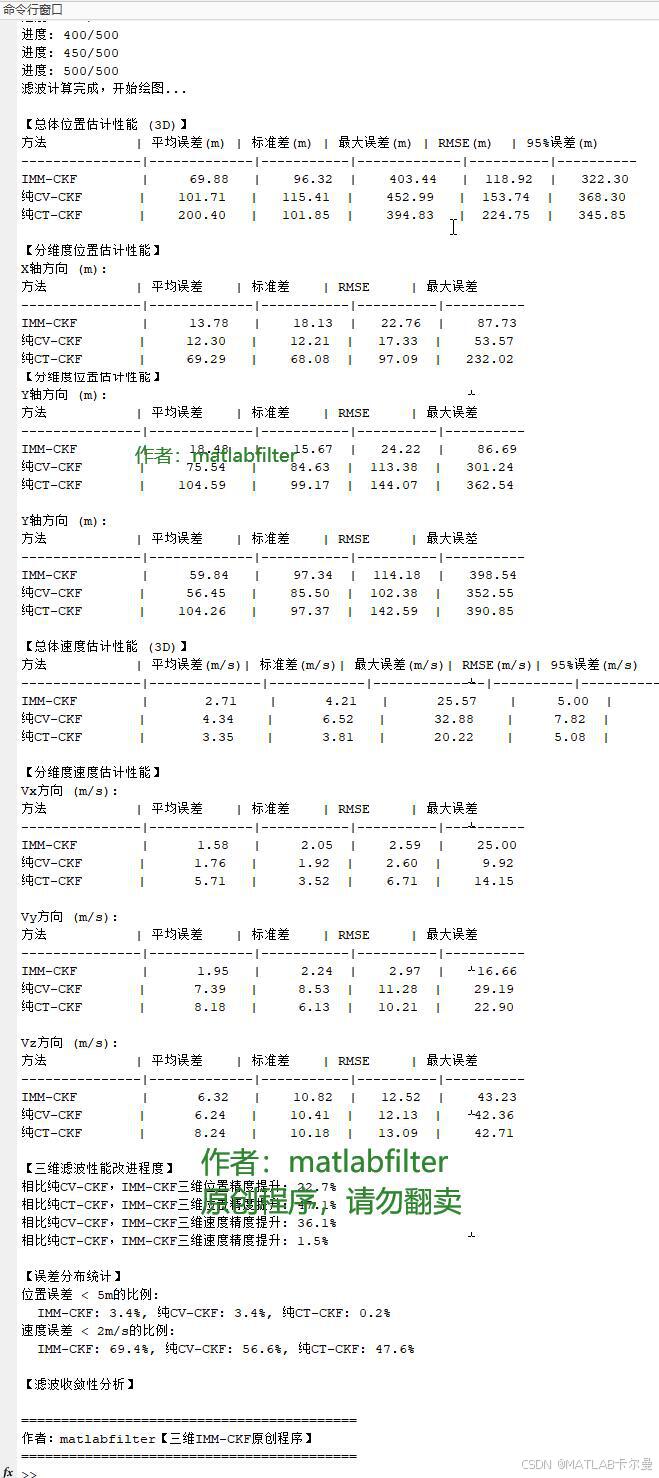
MATLAB源代码

程序结构：

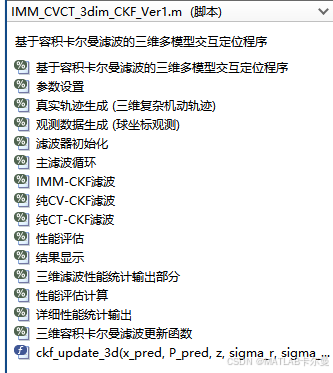
部分代码如下：

%% 基于容积卡尔曼滤波的三维多模型交互定位程序
% 包含CV(匀速)和CT(匀角速度转弯)模型，与单模型CKF对比
% 三维版本：状态[x,y,z,vx,vy,vz]，观测[r,θ,φ]（球坐标）
% 作者：matlabfilter
% 2025-07-22/Ver1

clear; clc; close all;
rng(0);
%% 参数设置
T = 1;                    % 采样时间
N = 500;                    % 仿真步数
omega = 0.08;               % CT模型角速度 (rad/s)

% 测量噪声参数
sigma_r = 3;                % 距离测量标准差
sigma_azimuth = 0.03;       % 方位角测量标准差 (rad)
sigma_elevation = 0.03;     % 俯仰角测量标准差 (rad)

% 过程噪声参数
q_cv = 0.1;                 % CV模型过程噪声强度
q_ct = 0.1;                 % CT模型过程噪声强度

% IMM参数
pi11 = 0.98; pi12 = 0.02;   % CV到CV和CV到CT的转移概率
pi21 = 0.03; pi22 = 0.97;   % CT到CV和CT到CT的转移概率
Pi = [pi11, pi12; pi21, pi22]; % 模型转移概率矩阵

mu = [0.6; 0.4];            % 初始模型概率

%% 真实轨迹生成 (三维复杂机动轨迹)
x_true = zeros(6, N);       % [x, y, z, vx, vy, vz]
x_true(:,1) = [0; 0; 100; 25; 5; 2]; % 初始状态（包含初始高度）

% 生成复合机动轨迹
for k = 2:N
    if k < N*0.3
        % CV模型 - 直线运动
        F_cv = [1, 0, 0, T, 0, 0;
                0, 1, 0, 0, T, 0;
                0, 0, 1, 0, 0, T;
                0, 0, 0, 1, 0, 0;
                0, 0, 0, 0, 1, 0;
                0, 0, 0, 0, 0, 1];
        x_true(:,k) = F_cv * x_true(:,k-1) + sqrt(q_cv)*[T^2/2*randn; T^2/2*randn; T^2/2*randn; T*randn; T*randn; T*randn];
    elseif k < N*0.7
        % CT模型 - 三维转弯运动（主要在水平面转弯，垂直方向有轻微变化）
        omega_true = omega * (1 + 0.3*sin(k*T));  % 时变角速度
        sin_wT = sin(omega_true*T);
        cos_wT = cos(omega_true*T);
        F_ct = [1, 0, 0, sin_wT/omega_true, -(1-cos_wT)/omega_true, 0;
                0, 1, 0, (1-cos_wT)/omega_true, sin_wT/omega_true, 0;
                0, 0, 1, 0, 0, T;
                0, 0, 0, cos_wT, -sin_wT, 0;
                0, 0, 0, sin_wT, cos_wT, 0;
                0, 0, 0, 0, 0, 1];
        % 添加垂直机动
        if k > N*0.4 && k < N*0.6
            x_true(6,k-1) = x_true(6,k-1) + 3*sin(k*T*0.1); % 垂直速度变化
        end
        x_true(:,k) = F_ct * x_true(:,k-1) + sqrt(q_ct)*[T^2/2*randn; T^2/2*randn; T^2/2*randn; T*randn; T*randn; T*randn];
    else
        % CV模型 - 再次直线运动
        F_cv = [1, 0, 0, T, 0, 0;
                0, 1, 0, 0, T, 0;
                0, 0, 1, 0, 0, T;
                0, 0, 0, 1, 0, 0;
                0, 0, 0, 0, 1, 0;
                0, 0, 0, 0, 0, 1];
        x_true(:,k) = F_cv * x_true(:,k-1) + sqrt(q_cv)*[T^2/2*randn; T^2/2*randn; T^2/2*randn; T*randn; T*randn; T*randn];
    end
end

%% 观测数据生成 (球坐标观测)

如需帮助，或有导航、定位滤波相关的代码定制需求，请点击下方卡片联系作者