强化学习笔记之浅谈ACKTR

最新推荐文章于 2023-12-30 14:28:41 发布

转载最新推荐文章于 2023-12-30 14:28:41 发布 · 2.2k 阅读

13 ·

CC 4.0 BY-SA版权

原文链接：https://zhuanlan.zhihu.com/p/122997370

Reinforcement learning 专栏收录该内容

41 篇文章

订阅专栏

本文深入解析了ACKTR算法，一种结合自然梯度和克罗内克积的Actor-Critic方法，旨在提高强化学习中的采样效率。通过简化Fisher信息矩阵的计算，ACKTR实现了对全连接神经网络参数的有效更新。

https://zhuanlan.zhihu.com/p/122997370

2017年NIPS上的文章"Scalable trust-region method for deep reinforcement learning using Kronecker-factored approximation"提出了一种 Actor Critic using Kronecker-Factored Trust Region(ACKTR)的方法，笔者发现这个方法被普遍引用，但关于论文中的一些细节问题，网上讲解的资料比较少，因此在这里尝试把个人对文章逻辑一些方面的理解写出来，希望可以帮助到其他阅读论文的朋友。

本文的行文顺序为：论文动机-->论文所用到的基本原理-->论文用法-->总结。

一、论文动机

（1）主要目的：为了更加高效地从样本中学习信息，提升采样效率（sample efficiency）。

（2）达到目的的手段：通过使用更高效的梯度更新算法（Natural gradient, 自然梯度）来更新网络的参数，以保证更高效地从样本中学习有效信息，减少对样本量的需求。

这里补充一点，在强化学习中通常认为off-policy的采样效率低于on-policy，因为off-policy中需要优化的目标策略（target policy）和执行动作的策略（behavior policy）不一致，从而导致了需要使用重要度采样（importance sampling）的方法来估计状态-值函数 [公式] ，而重要度采样又会引入偏差或者高方差的问题，使得样本利用率不是那么高。（这里不展开来写，想看具体原因的朋友可以参考【1】）

采样效率是很多强化学习方面的文章致力解决的问题，比如经典的改进ACER中针对off-policy的采样效率问题提出了重要度裁剪和偏差修正的方法，以保证off-policy在使用重要度采样的时候不至于给状态-值函数 [公式] 的估计带来过大的方差，同时对偏差也进行了修正。

补充上述信息是为了指出，有很多不同的手段都可以达到提升采样效率的目的，笔者认为ACKTR文章中的一个基本逻辑是：

为了提升采样效率--->可以通过减小样本量--->样本量减小就需要更高的学习效率--->使用更优的梯度更新算法提高学习效率

二、论文所用到的基本原理

ACKTR中主要用到了两个概念的基本原理：自然梯度的定义和克罗内克积（Kronecker product）的性质。

先介绍自然梯度。

现在知道了论文的目的并确定了达成该目的所采用的手段，就需要介绍ACKTR中运用了什么梯度更新算法来提高学习效率，这里就要介绍自然梯度的基本原理了。（以下主要是笔者个人的理解，没有非常艰深的数学推导，不涉及流形，如果理解有误，欢迎指出。）

在常见的优化问题中，通常会看到以下参数更新公式：

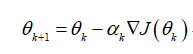
式（1）

这个优化公式很眼熟了，从负梯度的方向更新参数，目标是最小化函数 [公式] 。但是这个更新公式的目标函数的变化量和参数的变化量都是在同一个欧式空间中进行度量，参数变化的尺度通常使用欧式距离进行计算，例如：

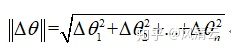
式（2）

那这种方式是有欠缺的，因为 [公式] 的增加量是使目标函数向最小的方向变动。这种度量参数变化的方式无法体现出参数变化引起的概率属性的变化量。

举个例子，假设有一个随机向量 [公式] ，以及生成这个随机向量的概率分布，现在参数发生了变化，，我们目前手里有的衡量工具是衡量在参数空间的变化尺度（见式（2）），但是却无法衡量这个参数变化对概率分布的影响。（用简单的例子想，就是一个高斯分布的均值和方差更新了，我们需要知道对这个高斯分布的影响有多大）

要衡量概率分布上的变化，最经典的方式就是采用KL散度（Bregman散度的特例）：

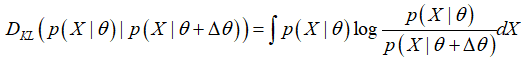
给出了两个概率分布之间的距离度量后，可以先简单地对自然梯度产生一个直观认识：

在欧式空间中，最速下降的方向就是负梯度方向，这是因为度量 [公式] 采用的是范数度量；现在度量方式到了概率分布的空间，最速下降的方向就是自然梯度的方向。

在计算自然梯度的表达式之前，无一例外地都需要化简一下KL散度的表达式。

首先，令 [公式] ，然后按照二阶泰勒展开式照抄代入：

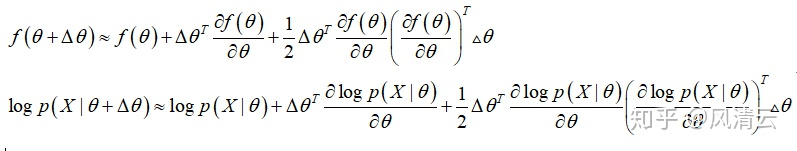
代入二阶泰勒展开式

把 [公式] 代入KL散度的表达式，那么KL散度的表达式就可以化简为：

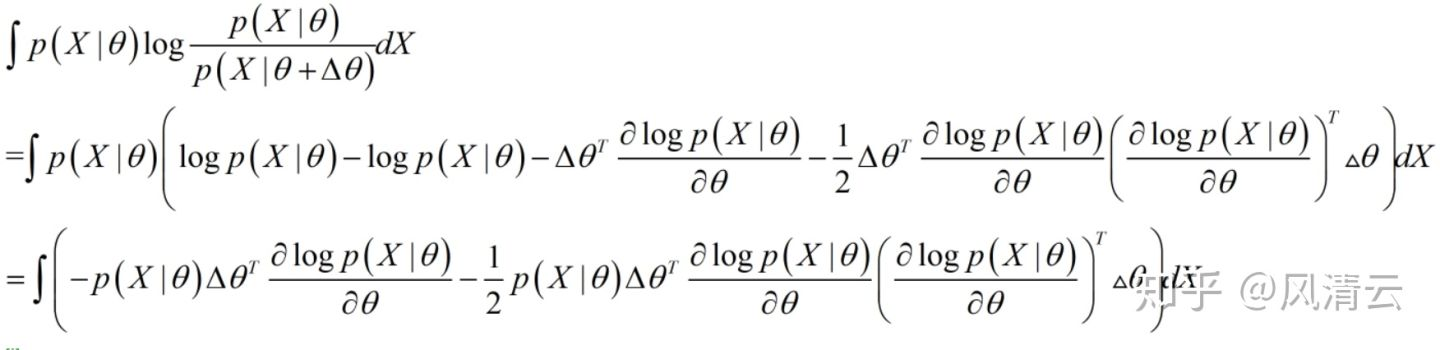
代入后简单的对数运算，看似复杂实则不然

然后下一步需要证明一下上式中的第一项的积分是为0的：

这下就得到了KL散度化简后的表达式了：

这中间的这个 [公式] 叫Fisher信息矩阵，它的定义是对数似然函数关于参数的导数的二阶矩，在上面的表达式中已经很明确了。想具体了解Fisher信息矩阵的定义可以知乎一下。

得到了KL散度化简后的表达式后，再回到优化目标上：

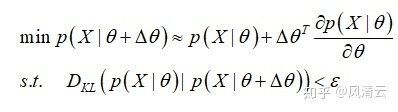
通过拉格朗日乘子法：

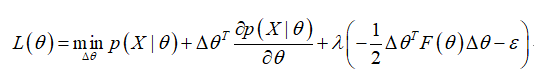
求偏导：

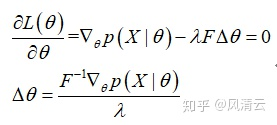
至此，就得到了自然梯度所表示的方向。

克罗内克积的定义和性质都比较简单，这里从百度百科直接摘出：

克罗内克积的定义

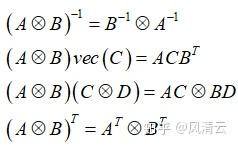
这里的vec(C)表示将一个m * n的矩阵向量化为一个 (m*n) * 1的列向量。

三、论文用法

ACKTR主要的贡献就是将自然梯度和克罗内克积应用到了actor-critic的参数更新上。但这中间还涉及到了一个减少计算量的操作，值得介绍一下。

对于一个全连接的神经网络（full-connected network, FCN）来说，假设有网络参数矩阵 [公式] ，输入层，输出层，假设激活函数是常数1，则有，损失函数为交叉熵损失。

那么损失关于网络参数的导数为：

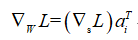
值得注意的是这里的维度，由于损失L是标量，对向量 [公式] 的导数自然和的维度相同，是m*1维的，而则是1*n维的，因此L关于参数的导数就是m*n维；

考虑到交叉熵损失最小化和二项分布似然函数的最大化是一致的，在这里就引入了概率分布函数，因此可以计算Fisher信息矩阵（括号内的展开就用到了克罗内克积的性质）：

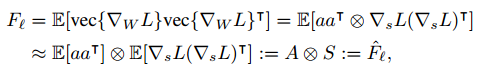
ACKTR中的技巧K-FAC

因此，参数矩阵 [公式] 就可以使用自然梯度进行更新了：

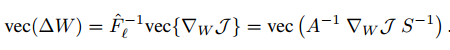
这里的简化主要在于简化了Fisher信息矩阵的求逆运算。原来的 [公式] 是一个(m*n)*(m*n)的矩阵，求逆的计算量非常大，简化之后变成了分别对一个n*n的矩阵和一个m*m的矩阵S求逆，计算量减少了不少。

至此，新的梯度更新算法也有了，关于FCN的参数更新的计算复杂度也减少了，就该应用到Actor-Critic中了：

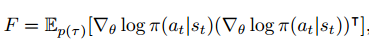
Actor的Fisher矩阵

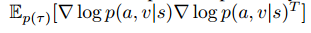
Critic的Fisher矩阵

四、总结

笔者个人看来，ACKTR中用到的自然梯度更新，克罗内克积简化参数更新的计算都是借鉴了他人的做法，但是ACKTR是首次将这两个技巧应用到了强化学习的Actor-Critic中的，提升了采样效率。

值得注意的是，Fisher信息矩阵和自然梯度更新都是要和概率分布挂钩的，不能滥用，ACKTR恰好就针对Actor和Critic中的概率分布应用了这两个技巧，也是非常巧妙的。

最后，毕竟是浅谈，如果理解有误，欢迎大家指出，谢谢~

参考文献：

【1】Sutton, Richard S., and Andrew G. Barto.Reinforcement learning: An introduction. MIT press, 2018.

【2】Wu, Yuhuai, et al. "Scalable trust-region method for deep reinforcement learning using kronecker-factored approximation."Advances in neural information processing systems. 2017.

【3】Martens, James, and Roger Grosse. "Optimizing neural networks with kronecker-factored approximate curvature."International conference on machine learning. 2015.