【从零开始的两轮自平衡车程序设计】04——控制算法之PID

总算是来到控制算法了，这是我买平衡车的本意，这一方面也正在继续学习中，能写到哪就写到哪吧，认识总算在更新，也希望和各位交流。
1.控制对象及模型
通过控制占空比，施加不同的等效电压在直流电机上，根据直流电机的电压电流关系，产生电流，电流产生转矩。
假定无打滑情况，转矩产生前向加速度，也产生使小车摆动的角加速度，这之间是复杂的耦合关系，可以通过受力分析或拉格朗日方程分析。具体分析我就直接贴图了。


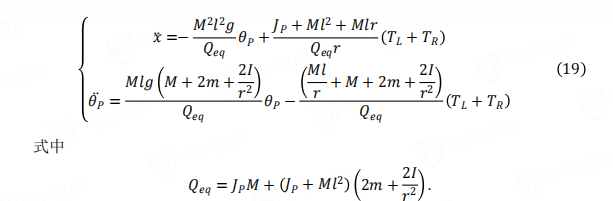
用拉格朗日方程分析

从结果来看，俯仰角和位移都是非线性的，而且位移x和俯仰角还有耦合，更糟糕的是我们不知道各个参数，所以，使用PID是简单而有效的，实践对比后也确实如此。
2.控制律：
姿态环：

姿态环只有PD，控制律中其实使用PD是最好的，因为不会导致系统升阶，但是D通常会有问题，因为如果通过俯仰角做差分，会把噪声放大，加滤波又带来延时，好在我们有陀螺仪。我经过测试，发现用陀螺仪的角速度比差分效果好，当然没有陀螺仪的话，用一些非线性的微分器也是可以做的。在这里要注意各个的极性，极性是非常重要，极性正确的话，调参是很快的。

速度环：

速度环是常规的PI，为什么上门用D，这里不用呢？我觉得如果用的也不一定不行，我后续有机会再试试。但是站在现代控制的角度，就能理解为什么是这么设计：

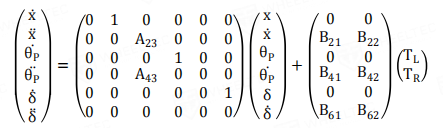
线性化后的状态方程可以这么写，如果不看转向环，即最后两个变量，那么这个状态方程的控制率设计为全状态反馈，通过配置好系数K，使得A-BKI的行列式全为负实数根，那么就收敛，这其实就是LQR是基础。那么可以看到，只要控制率是状态变量的线性组合，就能控制的住，对应这两个回路，就是PD和PI。

除此之外，有个反直觉的事，速度环是正反馈，而不是负反馈，这也是由于单输入多输出系统的影响，速度的方程中，通过姿态产生抑制项，从而保证稳定。

3.调节方法：
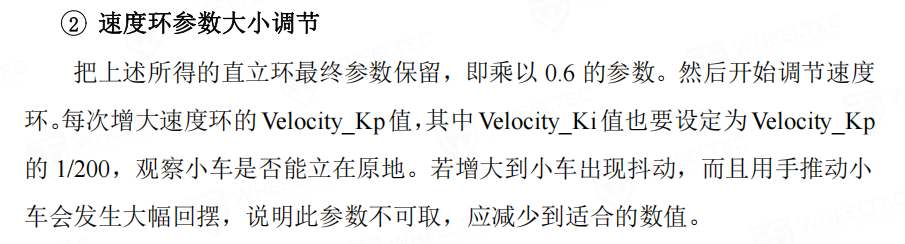
直接贴图了，重点就是，极性很重要。