1、外极几何
如果有一个场景的两个视图以及视图中的对应图像点,那么根据照相机间的空间相对位置关系、照相机的性质以及三维场景点的位置,可以得到对这些图像点的一些几何关系约束。
三维场景点XX经过4×4的单应性矩阵变换为HXHX后,则HXHX在照相机PH−1PH−1里得到的图像点和XX在照相机里得到的图像点相同。
λx=PX=PH−1HX=H^X^λx=PX=PH−1HX=H^X^
因此,当我们分析双视图几何关系时,总是可以将照相机间的相对位置关系用单应性矩阵加以简化。这里的单应性矩阵通常只做刚体变换,即值通过单应性矩阵变换了坐标系。一个比较好的做法是,将原点和坐标轴与第一个照相机对齐。
P1=K1[I|0]P1=K1[I|0]和P2=K2[R|t]P2=K2[R|t]
其中K1K1和K2K2是标定矩阵,RR是第二个照相机的旋转矩阵,是第二个照相机的平移向量。
同一个图像点经过不同的投影矩阵产生的不同投影点必须满足
xT2Fx1=0(*)(*)x2TFx1=0
其中:
F=K−T2StRK−11F=K2−TStRK1−1
矩阵StSt为反对称矩阵:
St=⎡⎣⎢0t3−t2−t30t1t2−t10⎤⎦⎥St=[0−t3t2t30−t1−t2t10]
公式∗∗为外极约束条件,矩阵为基础矩阵,基础矩阵可以由两照相机的参数矩阵(相对于旋转RR和平移)表示。由于det(F)=0det(F)=0,所以基础矩阵的秩小于等于2,我们将在估计FF的算法中用到这些性质。
上述公式表明,我们可以借助来恢复出照相机参数,而FF可以从对应的投影图像点计算出来。在不知道照相机内参数(和K2K2)的情况下,仅能恢复照相机的投影变换矩阵。在知道照相机内参数的情况下,重建是基于度量的。
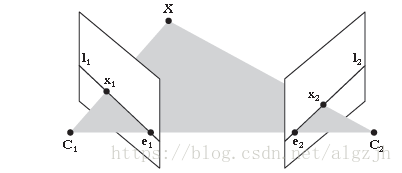
第二个视图中的图像点x2x2,利用公式∗∗,我们找到对应第一幅图像的一条直线:
其中lT1x1=0l1Tx1=0是第一幅图像中的一条直线。这条直线称为对应于点x2x2的外极线,点x2x2在第一幅图像中的对应点一定在这条直线上。所以,基础矩阵可以将对应点的搜索限制在外极线上。
外极线都经过一点ee,称为外极点(另一照相机光心对应的图像点),因为外极点在所有的外极线上,所以,因此,我们可以通过计算FF的零向量来计算出外极点。同理,另一个外极点可以通过计算得到。
2、计算FF:八点法
八点法是通过对应点来计算基础矩阵的算法。
外极约束可以写成线性系统的形式:
其中,ff包含的元素,Xi1=[xi1,yi1,wi1]X1i=[x1i,y1i,w1i]和Xi2=[xi2,yi2,wi2]X2i=[x2i,y2i,w2i]是一对图像点,共有nn对对应点。
基础矩阵中共有9个元素,由于尺度是任意的,所以只需要8个方程。
我们通常用SVD算法来计算最小二乘解。由于算法得出的解可能秩不为2(基础矩阵的秩小于等于2),所以我们通过将最后一个奇异值置0来得到秩最接近2的基础矩阵。
3、照相机和三维结构的计算
三角剖分
给定照相机参数模型,图像点可以通过三角剖分来恢复出这些点的三维位置。
对于两个照相机和P2P2的视图,三维实物点XX的投影为和x2x2
我们可以通过SVD算法来得到三维点的最小二乘估计值。
4、由三维点计算照相机矩阵
如果已经找到了一些三维点及其图像投影,我们可以使用直接线性变换的方法来计算照相机矩阵PP。本质上,这是三角剖分方法的逆问题,有时我们将其称为照相机反切法。利用该方法恢复照相机矩阵同样也是一个最小二乘问题。
每个三维点(齐次坐标下)按照投影到图像点xi=[xi,yi,1]xi=[xi,yi,1],相应的点满足下面的关系
其中,p1p1、p2p2和p3p3是矩阵PP的三行,上面的式子可以写得更紧凑,如下所示
然后,我们可以使用SVD分解估计出照相机矩阵。
5、由基础矩阵计算照相机矩阵
在两个视图的场景中,照相机矩阵可以由基础矩阵恢复出来。假设第一个照相机矩阵归一化为P1=[I|0]P1=[I|0],现在我们需要计算出第二个照相机矩阵P2P2,研究分为两类,未标定的情况和已标定的情况
(1)未标定的情况——投影重建
重建只能由射影变换计算出来
因此,在无标定的情况下,第二个照相机矩阵可以使用一个3×3的射影变换的得出,一个简单的方法是
P2=[SeF|e]P2=[SeF|e]
其中,ee是左极点,满足,SeSe是反对称矩阵。使用该矩阵做出的三角剖分很有可能会发生畸变,如倾斜的重建。
(2)已标定的情况——度量重建
在已标定的情况下,重建会保持欧式空间的一些度量特性。
给定标定矩阵KK,我们可以将它的逆作用于图像点xK=K−1xxK=K−1x,因此,在新的图像坐标系下,照相机方程变为
xk=K−1K[R|t]X=[R|t]Xxk=K−1K[R|t]X=[R|t]X
在新的图像坐标系下,点同样满足之前的基础矩阵方程
xTK2FxK1=0xK2TFxK1=0
在标定归一化的坐标系下,基础矩阵称为本质矩阵。为了区别未标定的情况,以及归一化了的图像坐标,我们通常将其记作EE,而非
6、多视图重建
SfM(Structure from Motion,从运动中恢复结构)
假设照相机已经标定,计算重建可以分为下面4个步骤:
(1)检测特征点,然后在两幅图像间匹配
(2)由匹配计算基础矩阵
(3)由基础矩阵计算照相机矩阵
(4)三角剖分这些三维点
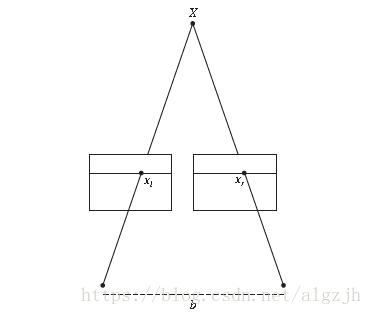
7、立体图像
Z=fbxl−xrZ=fbxl−xr
ff是经过矫正图像的焦距,是两个照相机中心之间的距离,xlxl和xrxr是左右两幅图像中对应点的xx坐标。分开照相机中心的距离称为基线。
8、计算视差图








 本文介绍多视图几何的基本原理,包括外极几何、基础矩阵计算、照相机矩阵恢复等内容,并探讨如何从多个视图中恢复三维结构。
本文介绍多视图几何的基本原理,包括外极几何、基础矩阵计算、照相机矩阵恢复等内容,并探讨如何从多个视图中恢复三维结构。
















 716
716

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








