【AI深究】CNN中的常用池化与下采样（Pooling & Downsampling）——全网最详细全流程详解与案例（附Python代码演示）|数学表达、主流变体与架构创新、优缺点与工程建议、调优技巧

大家好，我是爱酱。本篇将会系统梳理卷积神经网络（CNN）中的池化（Pooling）与下采样（Downsampling）机制，包括原理、数学表达、主流方法、实际案例、可视化代码演示与工程应用建议，配合数学公式，帮助你全面理解CNN特征压缩与空间不变性的关键技术。

注：本文章含大量数学算式、详细例子说明及大量代码演示，大量干货，建议先收藏再慢慢观看理解。新频道发展不易，你们的每个赞、收藏跟转发都是我继续分享的动力！

---

一、什么是池化与下采样？

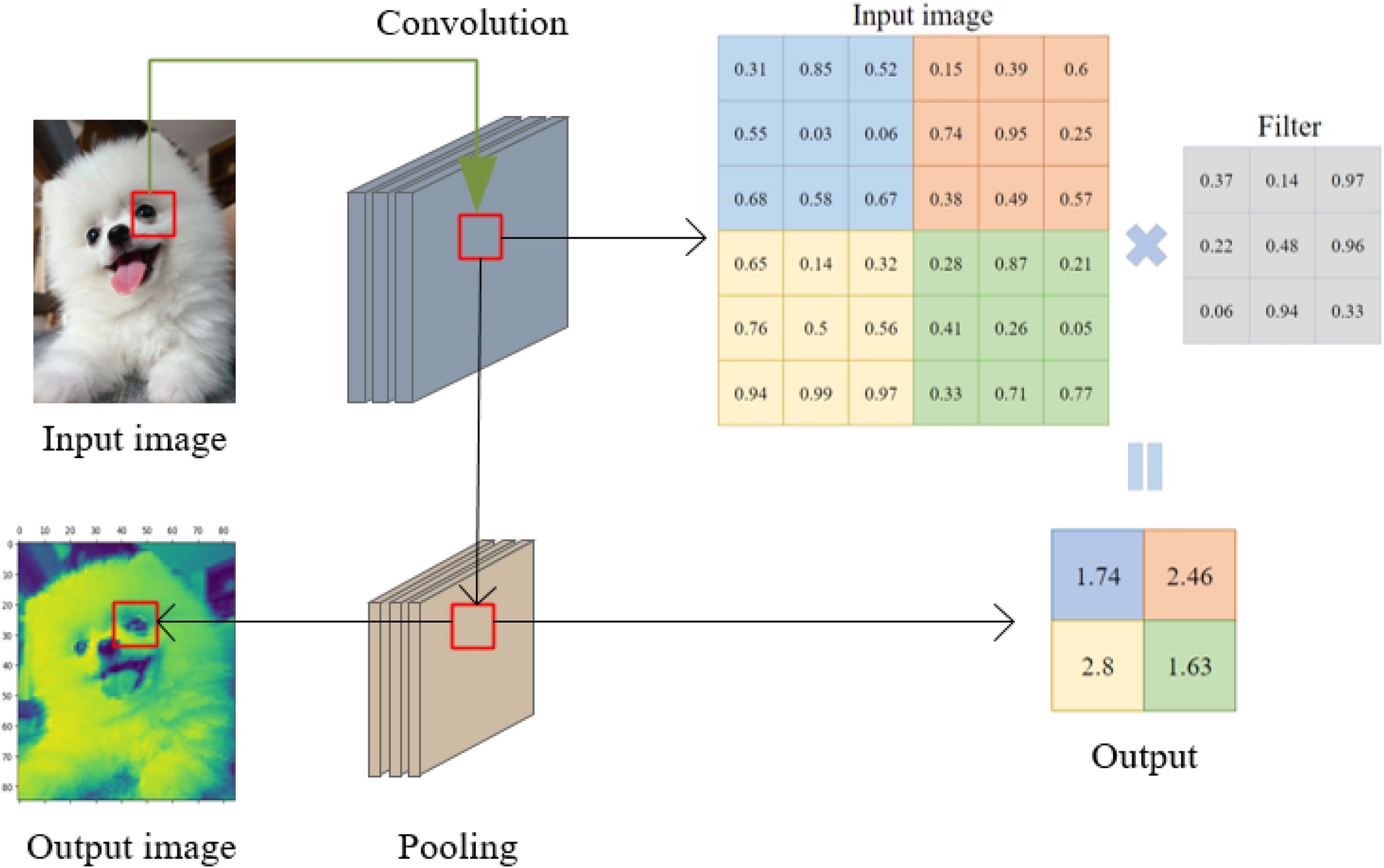
池化（Pooling）是CNN中用于降低特征图空间尺寸、减少参数和计算量、提升特征鲁棒性的重要操作。

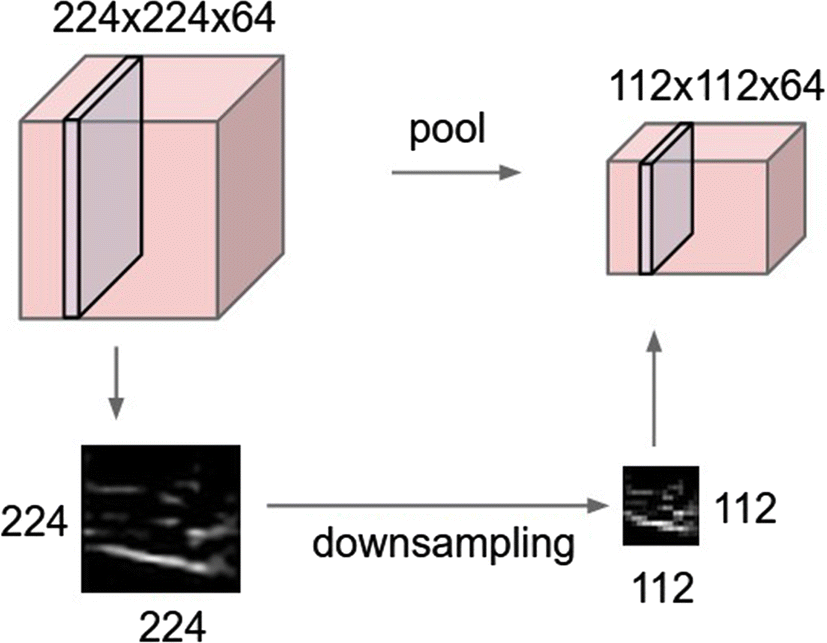
下采样（Downsampling）泛指所有降低数据分辨率的操作，池化是其最常见实现方式。

• 英文专有名词：Pooling, Downsampling, Max Pooling, Average Pooling, Global Pooling, Strided Convolution

• 本质作用：

  • 压缩特征图尺寸，减少后续层计算负担

  • 提取局部统计信息，提升模型对平移、旋转等扰动的鲁棒性

  • 防止过拟合，增强泛化能力

---

二、主流池化方法与数学表达

1. 最大池化（Max Pooling）

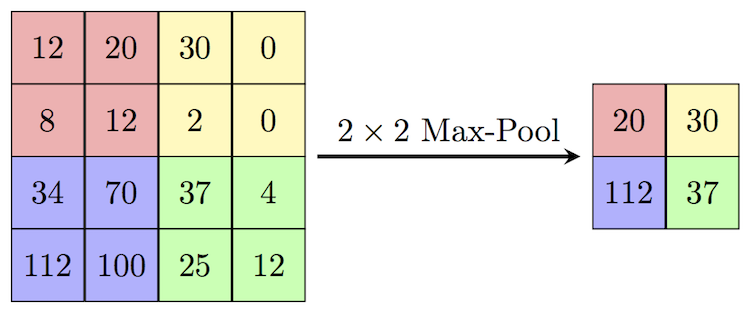
• 原理：在每个池化窗口内取最大值，突出显著特征。

• 数学表达：

  

  其中 为池化窗口， 为输入特征图， 为池化后输出。

2. 平均池化（Average Pooling）

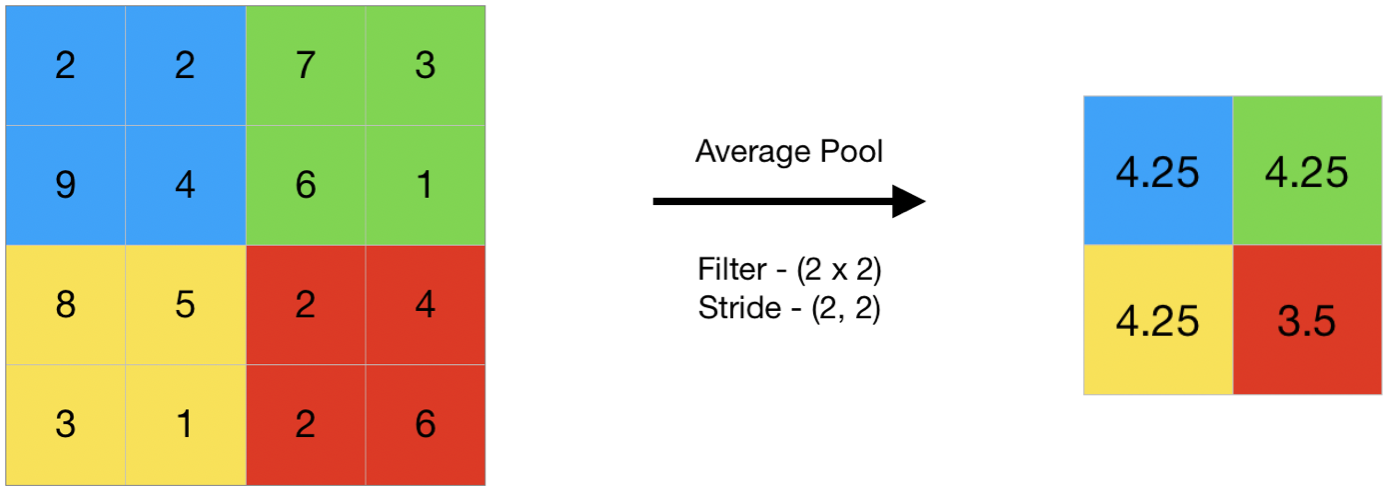
• 原理：在每个池化窗口内取均值，平滑特征响应。