【AI深究】前馈神经网络：Feedforward Neural Network（FNN）深度解析——全网最详细全流程详解与案例（附详尽Python代码演示）|优势局限与工程建议|常见变体结构|调优技巧

大家好，我是爱酱。本篇将会系统梳理Feedforward Neural Network（前馈神经网络，FNN）的原理、结构、数学表达、典型应用、可视化代码示例与工程实践，帮助你全面理解最基础也是最重要的神经网络架构。

注：本文章含大量数学算式、详细例子说明及大量代码演示，大量干货，建议先收藏再慢慢观看理解。新频道发展不易，你们的每个赞、收藏跟转发都是我继续分享的动力！

---

一、FNN的核心定义与结构

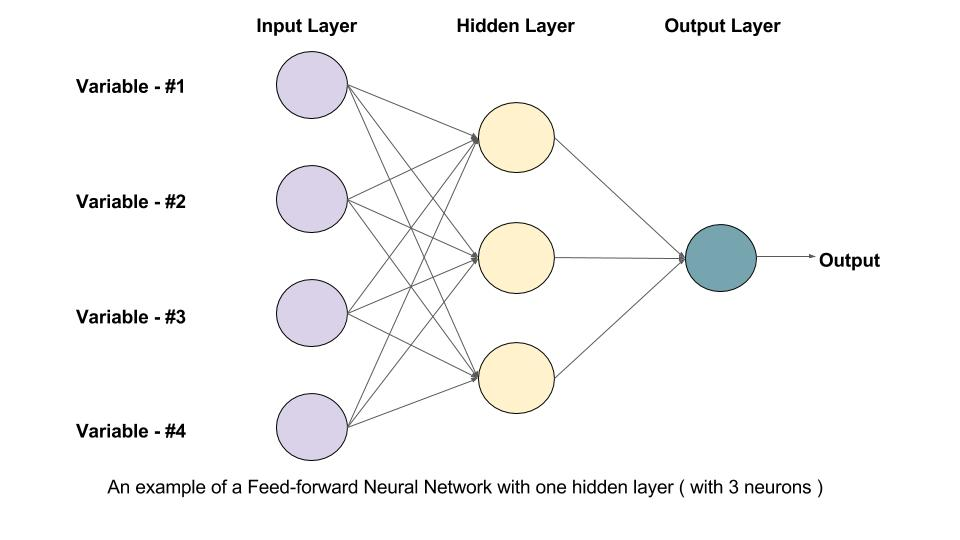
Feedforward Neural Network（FNN）是一种最基础的人工神经网络架构，信息流只沿一个方向——从输入层，经隐藏层，最终到输出层。网络中不包含任何环路或反馈连接。

• 英文专有名词：Feedforward Neural Network, FNN, Multilayer Perceptron (MLP)

• 结构组成：

  • 输入层（Input Layer）：接收原始特征，每个神经元对应一个输入变量。

  • 隐藏层（Hidden Layer）：一个或多个，负责特征抽象和非线性变换。

  • 输出层（Output Layer）：输出最终预测结果，神经元数目与任务类型有关（分类/回归）。

信息流动与激活函数

• 数据在各层间通过带权重的连接传递，每个神经元对输入做加权求和并加上偏置，再通过激活函数（Activation Function）引入非线性。

• 常用激活函数有：

  • Sigmoid: 

  • Tanh: 

  • ReLU: 

---

二、FNN的数学表达

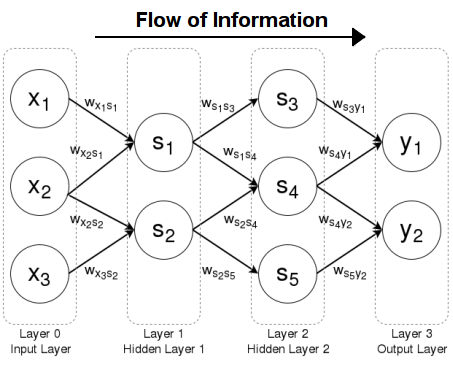
假设输入为 x∈Rnx∈Rn，网络有  层，每层权重

为 ，偏置为 ，激活函数为 ，则：

• 其中  为第