【AI概念】朴素聚类方法：层次聚类（Hierarchical Clustering）与密度聚类（Density-Based Clustering）有什么区别？算法流程数学推导、典型代码可视化、应用建议

大家好，我是爱酱。本篇将会系统讲解朴素聚类方法中的两大经典代表：层次聚类（Hierarchical Clustering）和密度聚类（Density-Based Clustering, 以DBSCAN为例）。内容包括基本原理、算法流程、数学表达、实际案例和工程应用，适合初学者和进阶读者。

注：本文章含大量数学算式、详细例子说明及大量代码演示，大量干货，建议先收藏再慢慢观看理解。新频道发展不易，你们的每个赞、收藏跟转发都是我继续分享的动力！

---

一、聚类是什么？

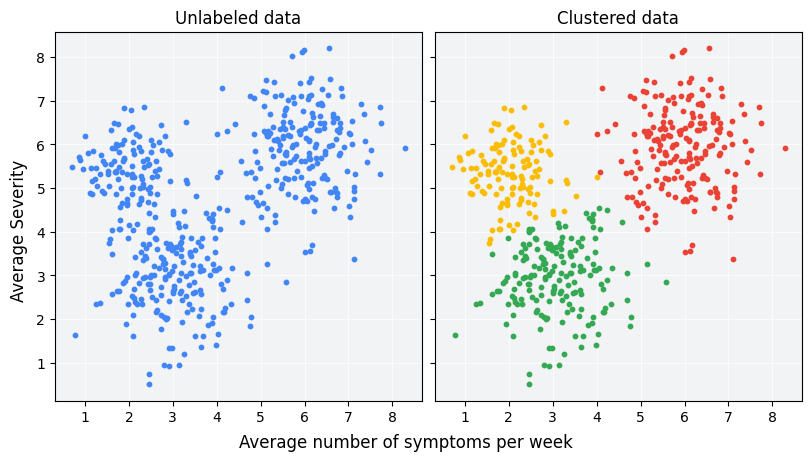
聚类（Clustering）是无监督学习中的一种基础任务，目标是将数据集中的样本按照相似性自动分组，使得同一组内的样本相似度高，不同组间的样本差异大。聚类广泛应用于数据探索、客户分群、图像分析、异常检测等领域。

---

二、层次聚类（Hierarchical Clustering）

1. 基本思想

层次聚类是一种通过构建“层级结构”来分组数据的无监督聚类方法。其核心思想是根据样本间的距离或相似度，逐步合并或分裂样本，最终形成一棵聚类树（dendrogram）。

• 凝聚型（自底向上，Agglomerative）：每个样本初始为一个单独的簇，逐步合并最近的两个簇，直到所有样本合并为一个簇或达到预设簇数。

• 分裂型（自顶向下，Divisive）：所有样本初始为一个大簇，逐步将簇拆分为更小的子簇，直到每个样本单独成簇或达到预设簇数。

2. 距离度量与合并准则

• 常用距离度量：欧氏距离、曼哈顿距离、余弦相似度等。

• 合并/分裂准则（Linkage）：

  • 最短距离（Single Linkage）：两簇最近点的距离。

  • 最长距离（Complete Linkage）：两簇最远点的距离。

  • 平均距离（Average Linkage）：两簇所有点对的平均距离。

  • 中心距离（Centroid Linkage）：簇中心之间的距离。

3. 算法流程（以凝聚型为例）

1. 计算所有样本对之间的距离，初始化每个样本为一个簇。

2. 找到距离最近的两个簇，合并为新簇。

3. 更新距离矩阵（根据选定的linkage方式）。

<