zz: http://zh.wikipedia.org/zh/%E5%85%8B%E7%BD%97%E5%86%85%E5%85%8B%E7%A7%AF
定义
如果A是一个 m × n 的矩阵,而B是一个 p × q 的矩阵,克罗内克积 则是一个 mp × nq 的分块矩阵
则是一个 mp × nq 的分块矩阵
更具体地可表示为
[编辑]例子
-
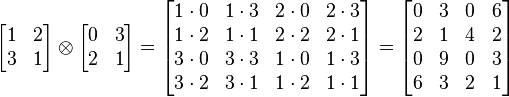 .
.
-
 .
.
[编辑]特性
[编辑]双线性和结合律
其中,A, B 和 C 是矩阵,而 k 是常量。
克罗内克积不符合交换律:通常,A  B 不同于 B
B 不同于 B  A。
A。
A  B和B
B和B  A是排列等价的,也就是说,存在排列矩阵P和Q,使得
A是排列等价的,也就是说,存在排列矩阵P和Q,使得
如果A和B是方块矩阵,则A  B和B
B和B  A甚至是排列相似的,也就是说,我们可以取P = QT。
A甚至是排列相似的,也就是说,我们可以取P = QT。
[编辑]混合乘积性质
如果A、B、C和D是四个矩阵,且矩阵乘积AC和BD存在,那么:
这个性质称为“混合乘积性质”,因为它混合了通常的矩阵乘积和克罗内克积。于是可以推出,A  B是可逆的当且仅当A和B是可逆的,其逆矩阵为:
B是可逆的当且仅当A和B是可逆的,其逆矩阵为:
[编辑]克罗内克和
如果A是n × n矩阵,B是m × m矩阵, 表示k × k单位矩阵,那么我们可以定义克罗内克和
表示k × k单位矩阵,那么我们可以定义克罗内克和 为:
为:









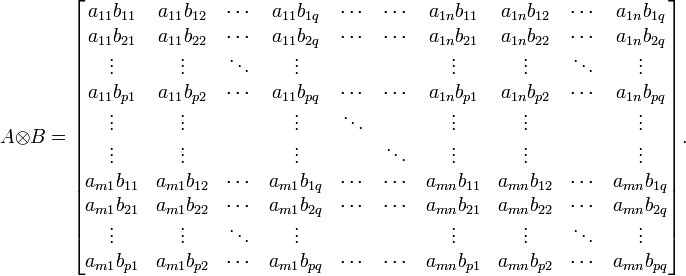
























 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








