计算机数值计算原理 | 整数浮点运算 / 常见谬误陷阱-优快云博客

注：本文为 “计算机数值计算” 相关合辑。
略作重排，如有内容异常，请看原文。

计算机是如何进行计算的？(一)

了不起的盖茨比。于 2022-03-03 15:30:17 发布

1. 写在前面

已知计算机的核心功能是数据的采集、处理与输出。但数据在计算机内部如何实现计算与处理，仍是待解答的关键问题。

2. 前言

计算机中的“字”由“位”构成，因此字可表示为二进制数。整数能够以十进制或二进制形式表示，但其他常用数值（如小数、大数等）的表示方式仍需明确，具体需解决以下问题：

如何表示小数及其他实数？
运算结果超出硬件可表示范围时，应如何处理？
硬件层面如何具体实现乘法与除法运算？

3. 加法和减法

加法是计算机的基础运算，其过程与手工计算一致：数字从右至左逐位相加，并将进位传递至左侧相邻位。减法运算同样通过加法实现，只需将被减数取反后与减数相加即可。

在这里插入图片描述

硬件的字长存在固定限制（如 64 位），当运算结果超出该限制时，会发生“溢出”。关于溢出的判定规则如下：

加法溢出判定：当两个不同符号的操作数相加时，不会发生溢出。因为此时总和的绝对值必然小于其中绝对值较大的操作数，不会超出字长限制；仅当两个同符号操作数相加时，才可能因总和绝对值超出字长而溢出。
减法溢出判定：当两个同符号的操作数相减时，不会发生溢出。因为同符号数相减本质上等价于异符号数相加，与加法中“异号数相加无溢出”的原理一致；仅当异符号数相减时，才可能发生溢出。

3.1 溢出的检测方法

加法溢出：若两个正数相加结果为负数，或两个负数相加结果为正数，则判定为溢出。
减法溢出：若正数减负数结果为负数，或负数减正数结果为正数，则判定为溢出。

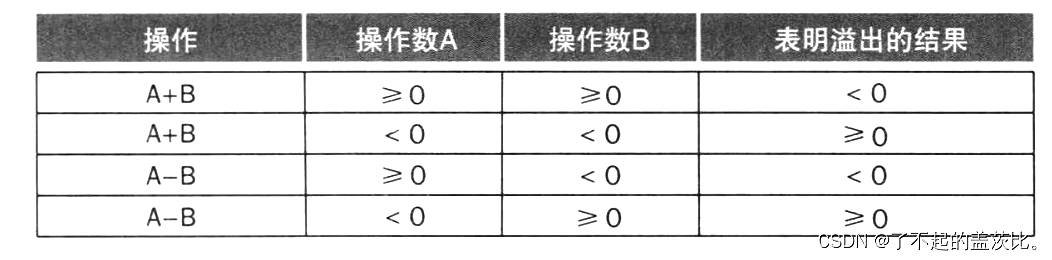
上述检测方法适用于二进制补码表示的有符号整数。对于无符号整数，其通常用于表示内存地址（忽略溢出），但编译器可通过分支指令轻松检测其溢出：

加法溢出：若总和小于任一加数，则判定为溢出。
减法溢出：若差值大于被减数，则判定为溢出。

3.2 小结

无论采用何种数值表示形式，计算机的有限字长决定了算术运算可能产生“溢出”（即结果超出固定字长的表示范围）。无符号数的溢出检测较简单，但因其常用于地址运算（程序通常无需检测地址溢出），故溢出常被忽略；二进制补码的溢出检测难度更高，但部分软件系统需识别溢出，因此当前所有计算机均支持溢出检测功能。

需注意：加法运算的速度取决于进位传递至高位的速度。现有多种进位预测方案可优化该速度，最坏情况下进位时间为加法器位长的 $log_2$ 函数。这类预测信号的速度更快（因需经过的逻辑门更少），但需额外的逻辑门以确保进位预测的准确性。

4. 乘法

首先回顾十进制手工乘法的步骤与操作数定义：乘法运算中，参与运算的两个数分别称为“被乘数”与“乘数”，运算结果称为“积”。手工乘法的核心步骤为：从右至左选取乘数的每一位，用该位与被乘数相乘，得到的中间结果相对于前一中间结果左移 1 位，最终将所有中间结果相加得到积。

请添加图片描述

4.1 乘法的位数特性

忽略符号位时， $n$ 位被乘数与 $m$ 位乘数的积需 $n + m$ 位表示（以覆盖所有可能结果）。因此，与加法类似，乘法也存在溢出问题——若用 64 位存储两个 64 位数的乘积（实际需 128 位），则会发生溢出。

4.2 二进制乘法的简化性

二进制数仅包含 0 和 1，因此每一步乘法可简化为两种操作：

若乘数位为 1，则将被乘数（即 $\times 被乘数$ ）复制到对应位置；
若乘数位为 0，则将 0（即 $\times 被乘数$ ）置于对应位置。

4.1 串行版的乘法算法及其硬件实现

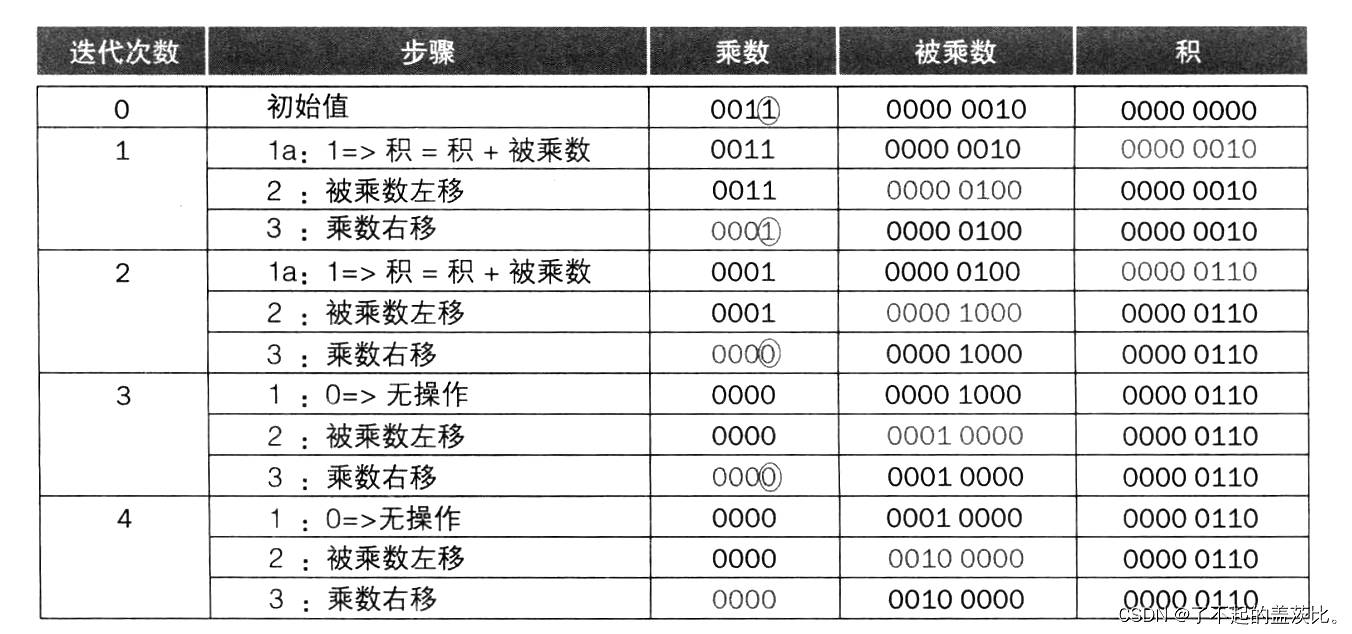
假设乘数存储于 64 位乘法寄存器，128 位乘积寄存器初始化为 0。根据手工乘法逻辑，每一步需将被乘数左移 1 位以与中间结果对齐，64 步后被乘数需左移 64 位，因此需 128 位被乘数寄存器（初始时右 64 位为被乘数，左 64 位为 0），每步左移 1 位以实现与乘积寄存器中间结果的对齐及累加。

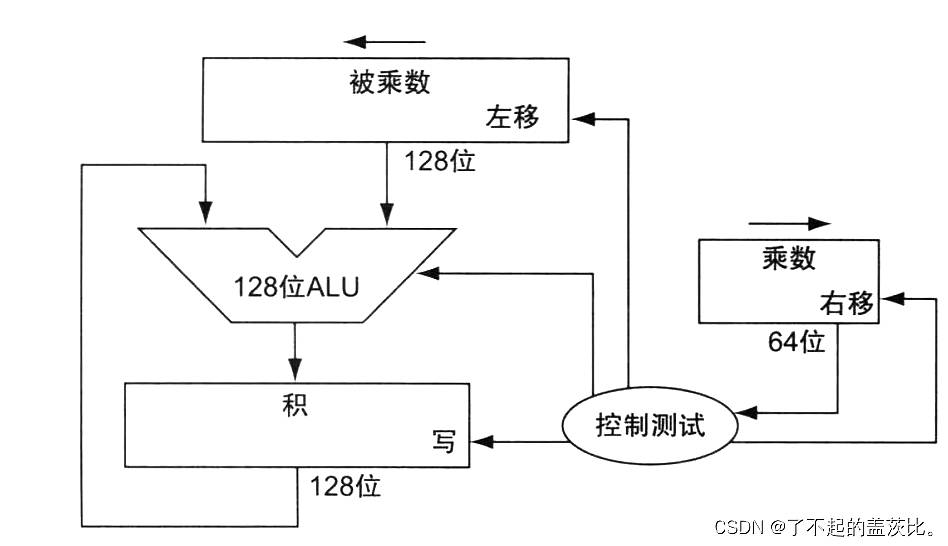
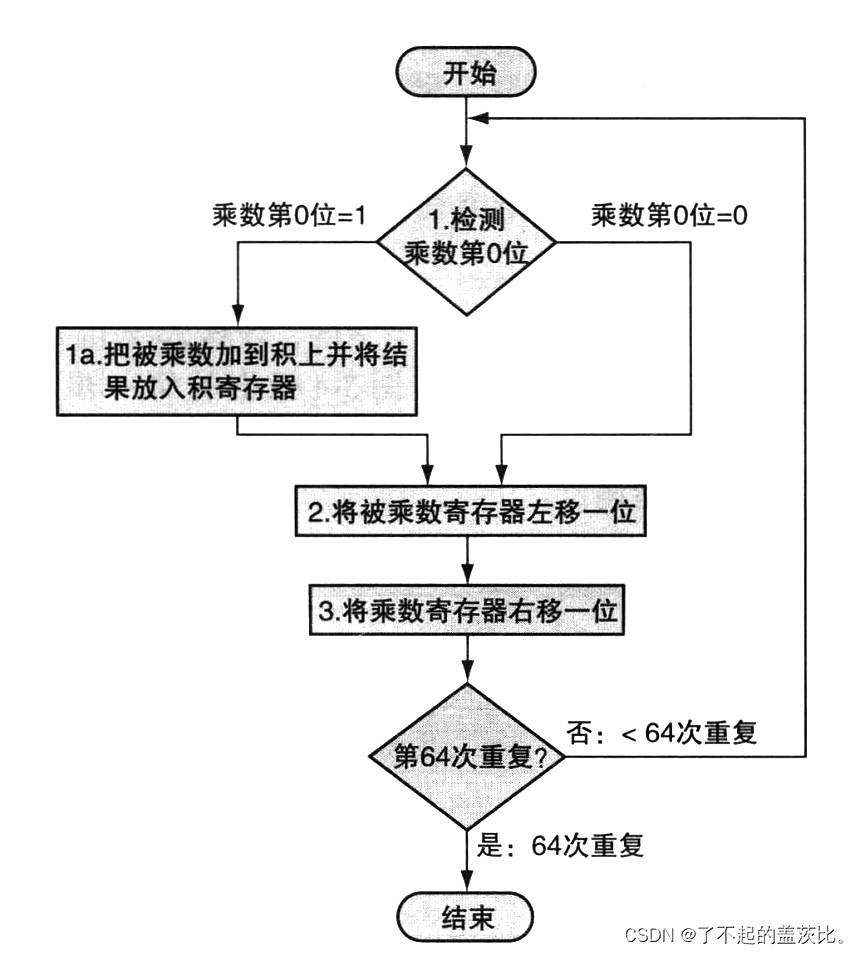
在这里插入图片描述

核心步骤（共 64 次迭代）

检测乘数最低位（第 0 位）：若为 1，则将被乘数加到乘积寄存器；若为 0，则不执行加法。
被乘数寄存器左移 1 位：模拟手工乘法中中间结果的左移操作。
乘数寄存器右移 1 位：为下一次迭代准备待检测的乘数位。

若每步耗时 1 个时钟周期，该算法计算两个 64 位数的乘积需约 200 个时钟周期。通过并行优化（如加法与移位操作并行执行），可将每步耗时降至 1 个时钟周期；进一步观察寄存器与加法器的未使用部分，可将其位长减半，以优化硬件结构。

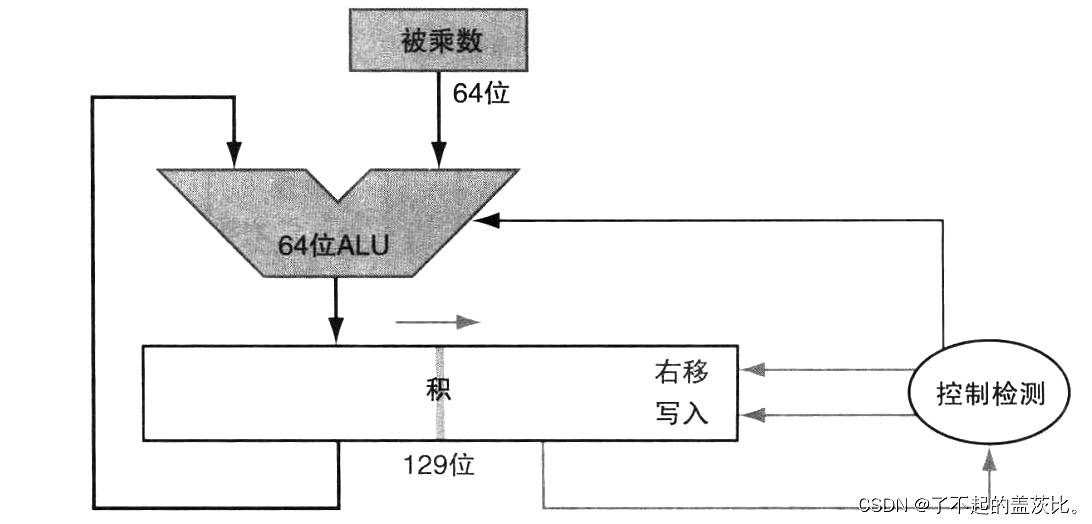
在这里插入图片描述

4.2 带符号乘法

带符号乘法的核心思路是“符号分离计算”：

先将被乘数与乘数转换为正数，记录其原始符号；
采用无符号乘法算法计算绝对值的乘积；
根据原始符号确定最终结果的符号（同号为正，异号为负）。

需注意：符号位不参与乘法运算，仅需对数值位迭代 31 次（针对 32 位系统）或 63 次（针对 64 位系统）。

4.3 快速乘法

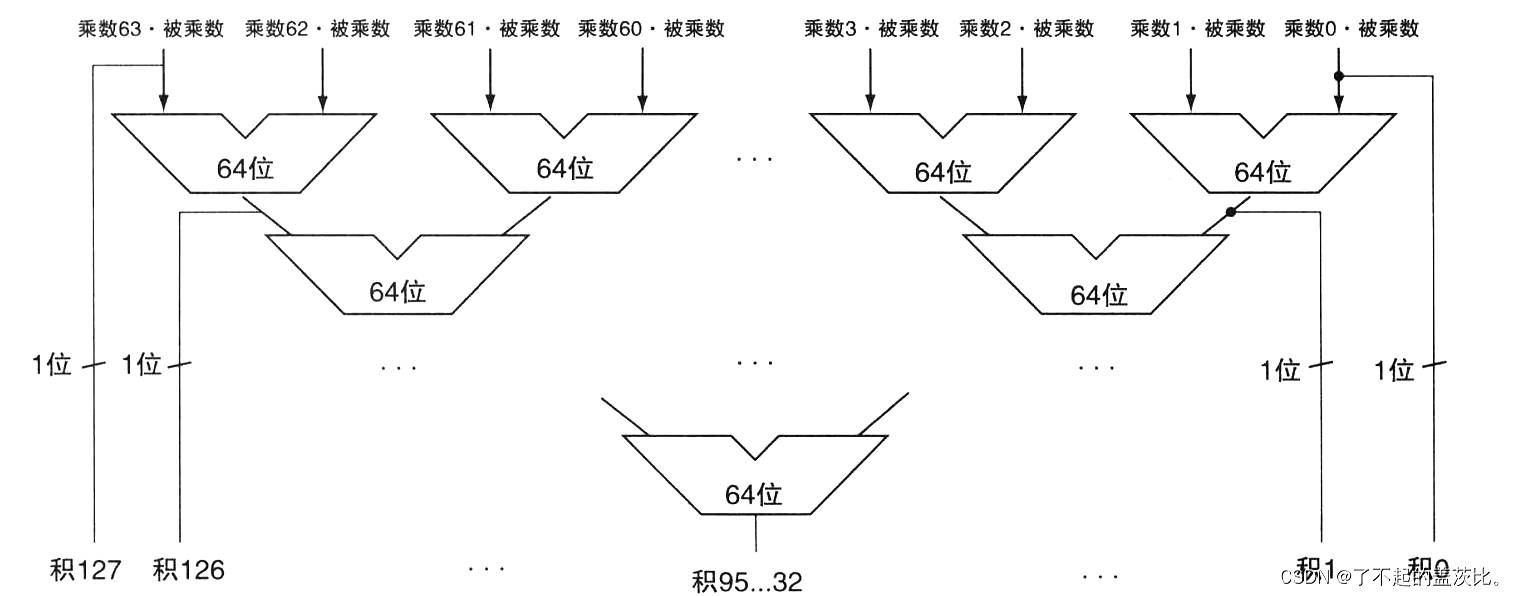
根据摩尔定律，硬件资源的丰富性使并行乘法成为可能。快速乘法的核心是“并行生成部分积并累加”：

同时检测 64 个乘数位，为每个乘数位配置一个 64 位加法器；
加法器的一个输入为“被乘数与对应乘数位的相与结果”（乘数位为 1 时为被乘数，为 0 时为 0），另一个输入为前一个加法器的输出；
将 64 个加法器组织为并行树结构，仅需等待 $log_2(64) = 6$ 次 64 位加法的时间（而非 64 次串行加法）。

实际应用中，通过“进位保留加法器”可进一步缩短乘法时间，且该结构易于流水化，支持同时处理多个乘法运算。

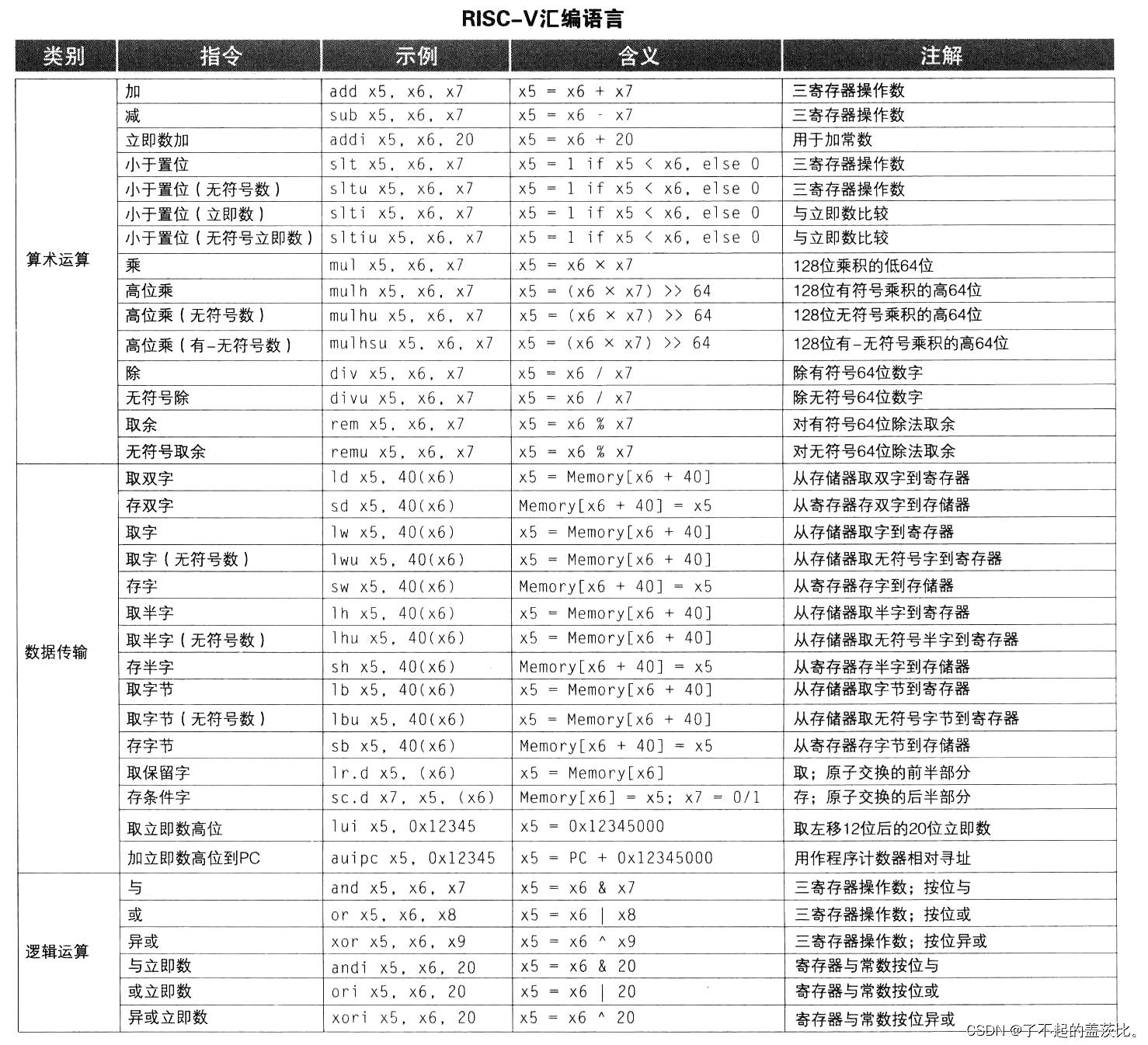
在这里插入图片描述

4.4 RISC-V 中的乘法

为生成 128 位带符号或无符号乘积，RISC-V 提供 4 条核心乘法指令，具体功能如下表所示：

指令	功能描述
`mul`	计算两个 64 位数的乘积，返回低 64 位结果（适用于获取 64 位整数积）
`mulh`	计算两个带符号 64 位数的乘积，返回高 64 位结果
`mulhu`	计算两个无符号 64 位数的乘积，返回高 64 位结果
`mulhsu`	计算一个带符号、一个无符号 64 位数的乘积，返回高 64 位结果

4.5 总结

乘法硬件的核心逻辑是“移位与累加”，编译器甚至可直接使用移位指令实现“乘以 $2$ 的幂”的运算（如左移 $k$ 位等价于乘以 $2^k$ ）。通过增加硬件资源实现并行加法，可显著提升乘法运算速度。

5. 除法

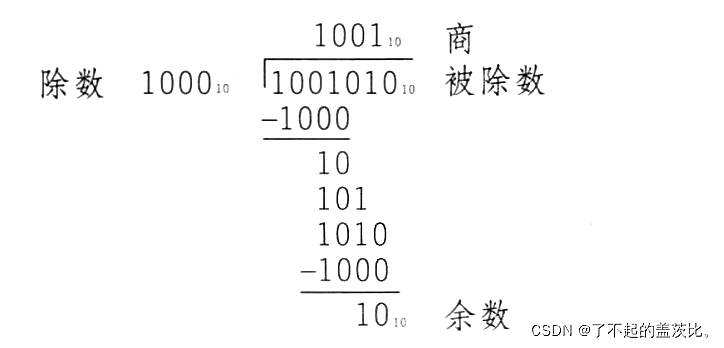
除法是乘法的逆运算，其使用频率较低且存在特殊情况（如除以 0 为无效操作）。首先回顾十进制手工长除法的操作数定义：参与运算的两个数分别称为“被除数”与“除数”，运算结果分为“商”（整数部分）和“余数”（剩余部分），三者满足关系式：
$\text{被除数} = \text{商} \times \text{除数} + \text{余数}$
其中，余数的绝对值小于除数。部分程序会仅使用除法指令获取余数，而忽略商。

在这里插入图片描述

5.1 二进制除法的简化性

二进制数仅包含 0 和 1，因此每一步仅需判断“除数能否从当前被除数中减去”：若能，则商的对应位为 1；若不能，则为 0，简化了除法运算逻辑。

5.1 除法算法及其硬件实现

假设商寄存器（64 位）初始化为 0，除数需存储于 128 位除数寄存器的左半部分（每步右移 1 位以与被除数对齐），余数寄存器初始化为被除数（64 位，左 64 位补 0）。

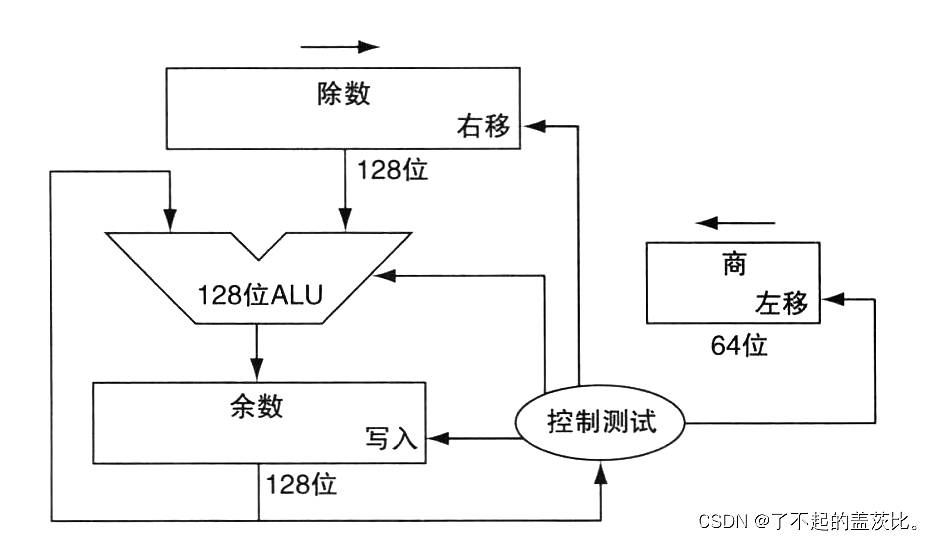
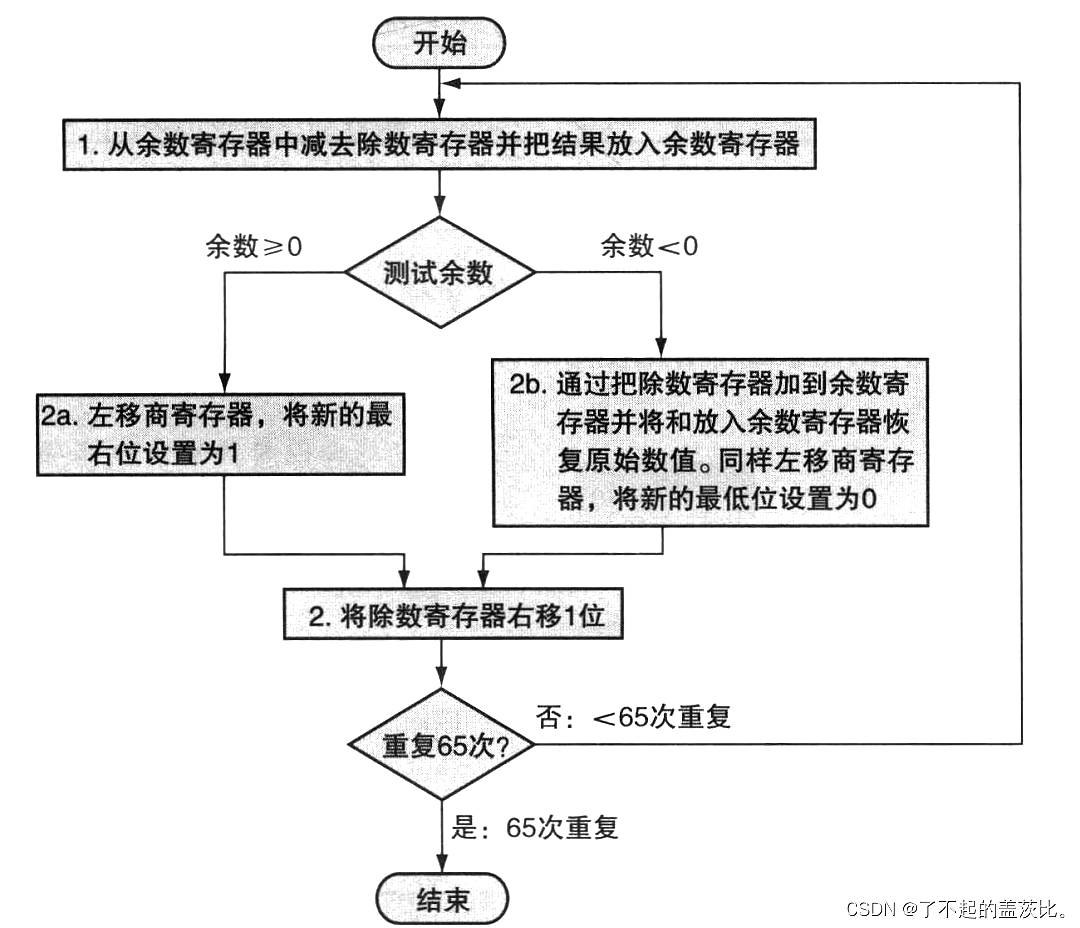
在这里插入图片描述

核心步骤（共 64 次迭代）

余数寄存器减去除数寄存器的左半部分（实现“比较除数与当前余数”）；
判定减法结果：
- 若结果为正（或零）：说明除数小于等于当前余数，将商寄存器的最低位置 1（步骤 2a）；
- 若结果为负：说明除数大于当前余数，将除数加回余数以恢复原始值，并将商寄存器的最低位置 0（步骤 2b）；
除数寄存器右移 1 位，为下一次迭代对齐除数与余数；
商寄存器左移 1 位，为下一次商位预留位置。

迭代完成后，余数寄存器存储最终余数，商寄存器存储最终商。通过“移位、减法与商位更新并行执行”及“减半加法器与寄存器位长”，可进一步优化算法速度与硬件成本。

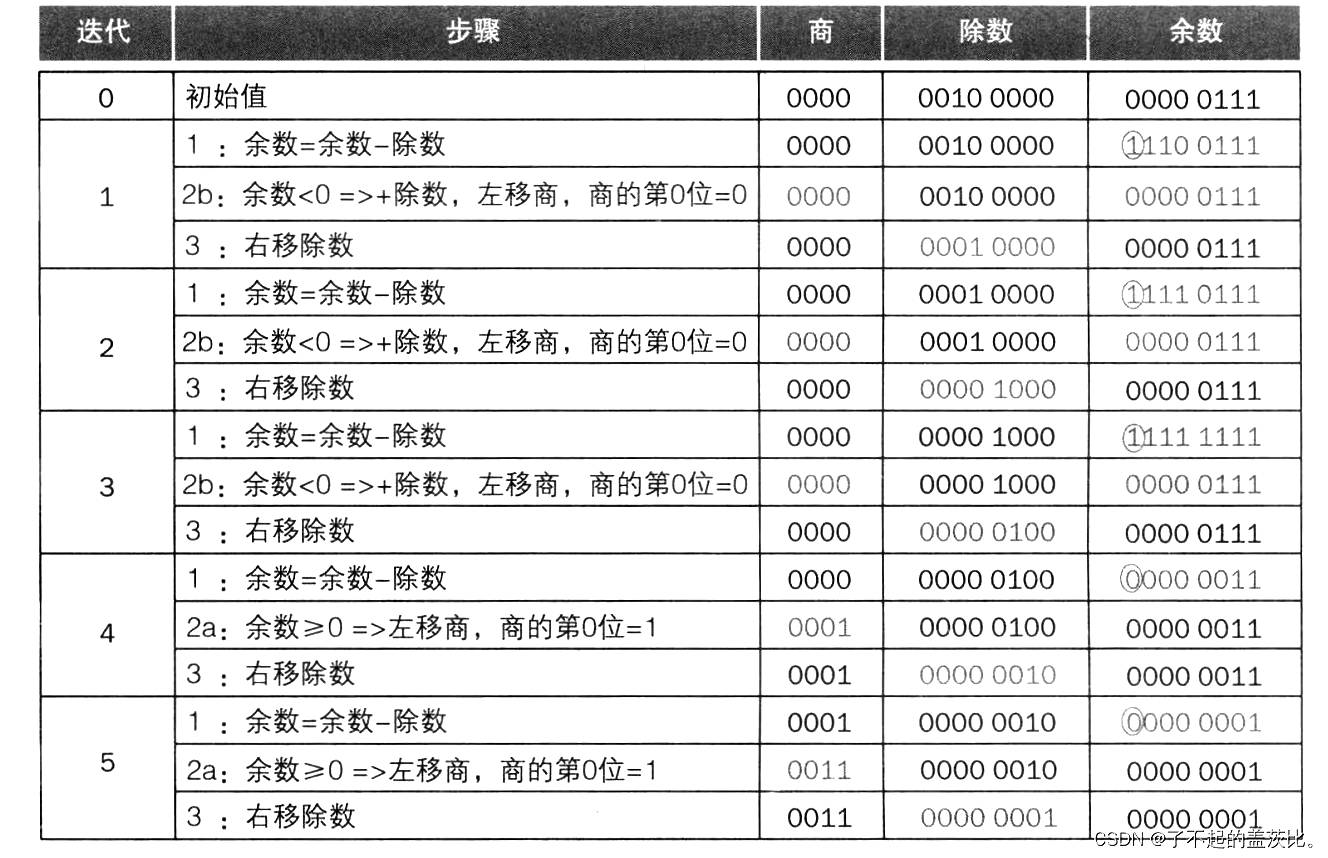
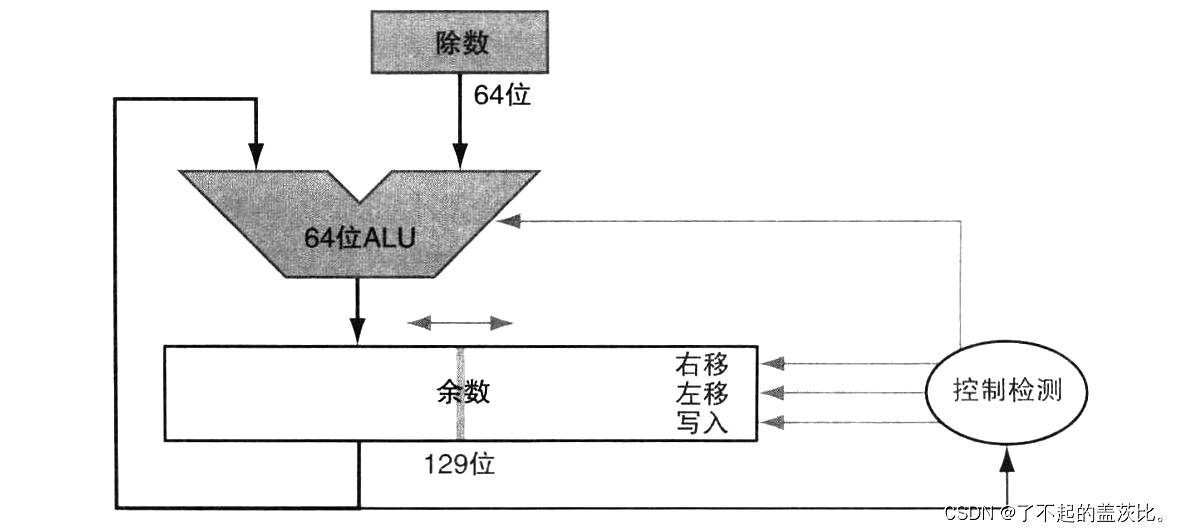
在这里插入图片描述

5.2 有符号除法

有符号除法的核心规则是“符号分离计算 + 余数符号与被除数一致”：

记录被除数与除数的原始符号，将两者转换为正数后执行无符号除法；
根据原始符号确定商的符号（同号为正，异号为负）；
调整余数的符号，使其与被除数的符号一致（即使商的绝对值发生微小调整，也需满足

$\text{被除数} = \text{商} \times \text{除数} + \text{余数}$ 且 $|\text{余数}| < |\text{除数}|$ ）

示例（以 $\pm7 \div \pm2$ 为例）

$\div +2$ ：商 = $+ 3$ ，余数 = $+ 1$ （满足 $\times 2 + 1$ ）；
$\div +2$ ：商 = $- 3$ ，余数 = $- 1$ （满足 $\times 2 + (-1)$ ）；
$\div -2$ ：商 = $- 3$ ，余数 = $+ 1$ （满足 $\times (-2) + 1$ ）；
$\div -2$ ：商 = $+ 3$ ，余数 = $- 1$ （满足 $\times (-2) + (-1)$ ）。

5.3 快速除法

与乘法不同，除法难以通过简单的并行加法加速——因为每一步需依赖前一步减法结果的符号（无法并行生成所有商位）。当前快速除法的核心思路是“预测多位商并纠正错误”，通过预先猜测 2~4 位商，再根据实际结果调整，以减少迭代次数，提升速度。

5.4 RISC-V 中的除法

为处理有符号与无符号整数除法，RISC-V 提供 4 条核心除法与余数指令，具体功能如下表所示：

指令	功能描述
`div`	计算两个带符号 64 位数的商，返回整数商（截断为 0 方向）
`divu`	计算两个无符号 64 位数的商，返回整数商
`rem`	计算两个带符号 64 位数的余数，余数符号与被除数一致
`remu`	计算两个无符号 64 位数的余数

5.5 总结

RISC-V 为乘法与除法提供独立的 64 位寄存器支持。除法运算的加速依赖于“多位商预测与纠错”，通过减少迭代次数提升运算效率。

在这里插入图片描述

6. 写在最后

前文已完整介绍整数的加法、减法、乘法与除法运算，下一节将聚焦浮点数的计算方法，包括浮点表示、加法、减法、乘法与除法。

计算机是如何进行计算的？(二)

了不起的盖茨比。已于 2022-03-04 16:19:01 修改

1. 写在前面

上一节已介绍整数的加法、减法、乘法与除法运算，本节将系统讲解浮点数的表示方法及四则运算。

2. 浮点运算

除有符号与无符号整数外，编程语言还支持小数（数学中称为“实数”）。实数的表示通常采用“科学记数法”——小数点左侧仅保留 1 个非零数字，此类表示称为“规格化数”（无前置零）。

对于二进制数，规格化的定义为：通过调整指数（即移位），使二进制小数点左侧仅保留 1 个非零数字（即 1）。此时，二进制小数点称为“二进制小数点”，支持此类数值的运算称为“浮点运算”（因二进制小数点位置可通过指数调整，并非固定），以区别于整数的“定点表示”。

2.1 浮点表示的核心优势

采用规格化科学记数法表示实数，具有以下三个核心优势：

简化数据交换：统一的表示格式使不同系统间的浮点数数据传输更便捷；
简化运算算法：规格化形式为浮点加法、乘法等运算提供统一的操作逻辑；
提升存储精度：消除无用的前置零，将节省的位用于存储更多有效数字，提高数据精度。

2.2 浮点表示的结构平衡

浮点数的表示需在“尾数字段”与“指数字段”的位数之间做平衡——固定字长下，若尾数字段增加 1 位，指数字段需减少 1 位，两者的功能差异如下：

尾数字段：存储小数部分（通常取值范围为 $[0, 1)$ ），位数越多，小数精度越高；
指数字段：存储指数（含符号），位数越多，可表示的数值范围越大（即能表示更大或更小的数）。

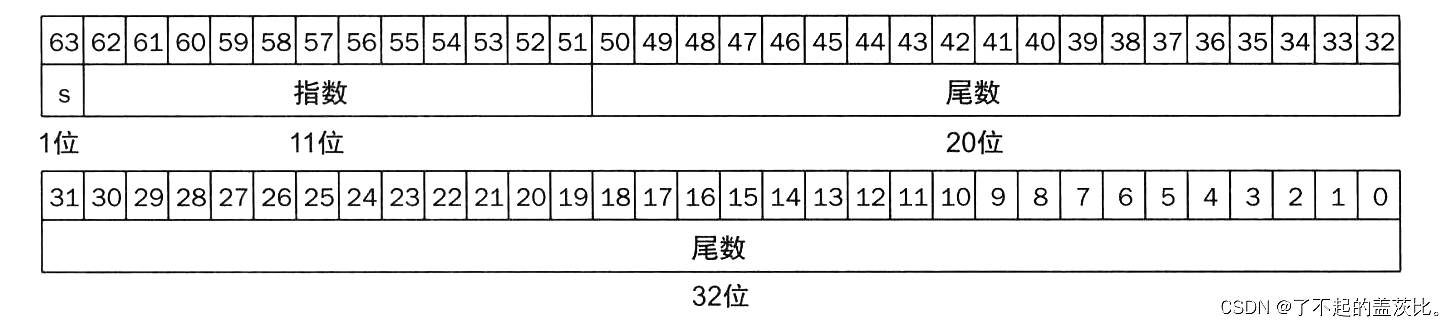
浮点数通常占用多个字长，以 RISC-V 采用的单精度浮点数（32 位）为例，其结构如下：

符号位（s）：1 位，1 表示负数，0 表示正数；
指数字段：8 位，存储带偏移的指数（用于扩大表示范围）；
尾数字段：23 位，存储小数部分（隐含整数部分为 1，见 2.3 节 IEEE 754 标准）。

这种“符号与数值分离”的表示方法称为“符号-数值表示法”。

在这里插入图片描述

2.2.1 单精度与双精度的范围差异

为扩大数值表示范围，引入“双精度浮点数”（64 位），其结构为：1 位符号位、11 位指数字段、52 位尾数字段。两种精度的数值范围对比如下：

单精度：可表示的数值范围约为 $\times 10^{-38}$ 至 $\times 10^{38}$ ；
双精度：可表示的数值范围约为 $\times 10^{-308}$ 至 $\times 10^{308}$ 。

在这里插入图片描述

需注意：浮点数的“溢出”分为两种情况：

上溢：数值过大，超出指数字段可表示的最大指数；
下溢：数值过小，超出指数字段可表示的最小指数（通常将下溢结果视为 0）。

2.3 IEEE 754 浮点数标准

RISC-V 的浮点格式遵循 IEEE 754 标准（1980 年后几乎所有计算机均采用该标准），其核心改进是“隐含整数位 1”，以进一步提升精度。

2.3.1 标准表示公式

IEEE 754 规格化浮点数的表示公式为：
$(-1)^s \times (1 + F) \times 2^E$
其中：

$s$ ：符号位（0 为正，1 为负）；
$F$ ：尾数字段的值（ $\leq F < 1$ ），若尾数字段的各位从左至右为 $f_1, f_2, ..., f_{23}$ （单精度），则 $f_1 \times 2^{-1} + f_2 \times 2^{-2} + ... + f_{23} \times 2^{-23}$ ；
$E$ ：指数字段对应的实际指数（需通过偏移值调整，见 2.3.3 节）。

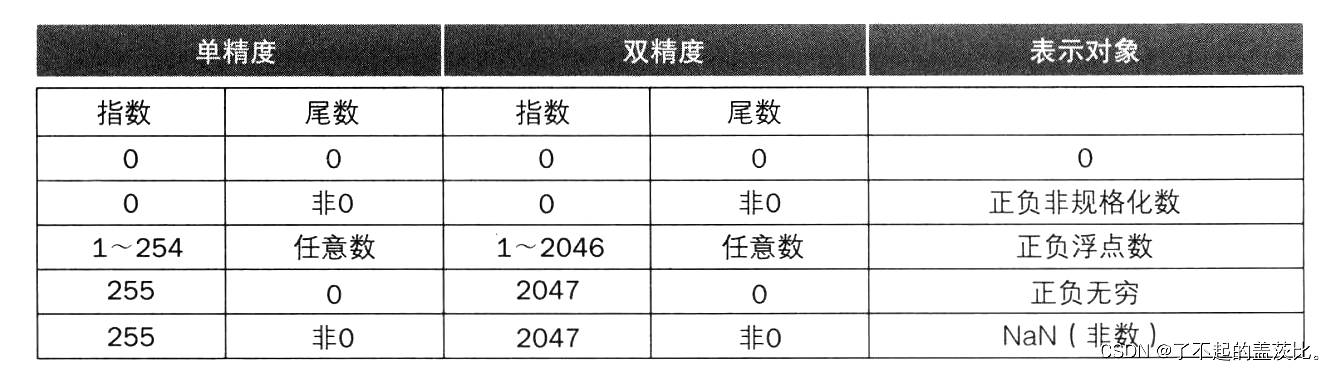
在这里插入图片描述

2.3.2 特殊值表示

IEEE 754 标准还定义了特殊值，以处理异常运算结果：

NaN（Not a Number）：表示无效运算结果，如 $0/0$ 、 $\infty - \infty$ 等；
无穷大（ $\infty$ ）：表示超出最大范围的正数或负数（如 $1/0$ 为 $+\infty$ ， $- 1/0$ 为 $-\infty$ ）。

2.3.3 指数的偏移表示

为简化浮点数的排序（可复用整数比较硬件），IEEE 754 采用“偏移表示法”存储指数——将实际指数加上一个固定偏移值，转化为无符号数存储，规则如下：

单精度：偏移值为 127，即存储的指数值 = 实际指数 $E + 127$ ；
双精度：偏移值为 1023，即存储的指数值 = 实际指数 $E + 1023$ 。

偏移表示法的优势：最小负指数对应存储值为 0，最大正指数对应存储值为全 1，确保“指数越大，存储的无符号数越大”，与整数比较逻辑一致。

例如：单精度下，实际指数 $E = - 1$ 时，存储值为 $- 1 + 127 = 126$ （二进制 01111110）；实际指数 $E = 1$ 时，存储值为 $1 + 127 = 128$ （二进制 10000000），符合“指数越大，存储值越大”的逻辑。

2.3.4 浮点表示示例（以十进制 -0.75 为例）

以单精度和双精度格式表示十进制数 $- 0.75$ ，步骤如下：

十进制转二进制： $-0.75_{10} = -3/4_{10} = -11_2 / 2^2_{10} = -0.11_2$ ；
规格化二进制： $-0.11_2 = -1.1_2 \times 2^{-1}$ （满足“小数点左侧仅 1 个非零数字”）；
匹配 IEEE 754 公式：
- 符号位 $s = 1$ （负数）；
- 尾数字段 $F = 0.1_2$ （因 $1 + F = 1.1_2$ ，故 $F = 0.1_2$ ，单精度下尾数字段补 22 个 0，即 100...000（共 23 位））；
- 实际指数 $E = - 1$ ，单精度存储指数值 = $- 1 + 127 = 126$ （二进制 01111110）；
单精度最终表示：符号位 1 + 指数 01111110 + 尾数 100...000，即二进制 10111111010000000000000000000000；
双精度表示：偏移值为 1023，存储指数值 = $- 1 + 1023 = 1022$ （11 位二进制 01111111110），尾数字段 $F = 0.1_2$ （补 51 个 0，共 52 位），最终为符号位 1 + 指数 01111111110 + 尾数 100...000。

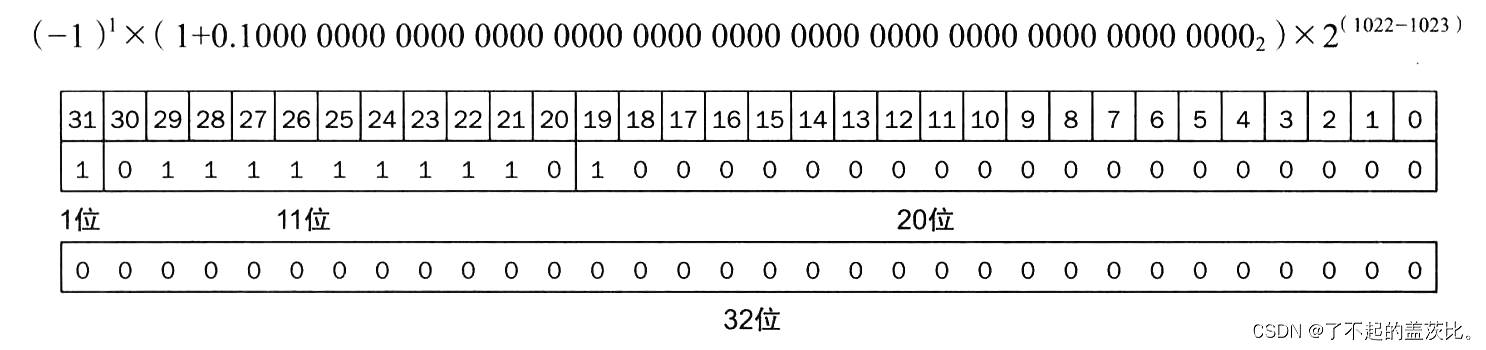
在里插入图片描述

将二进制浮点数转换为十进制浮点数

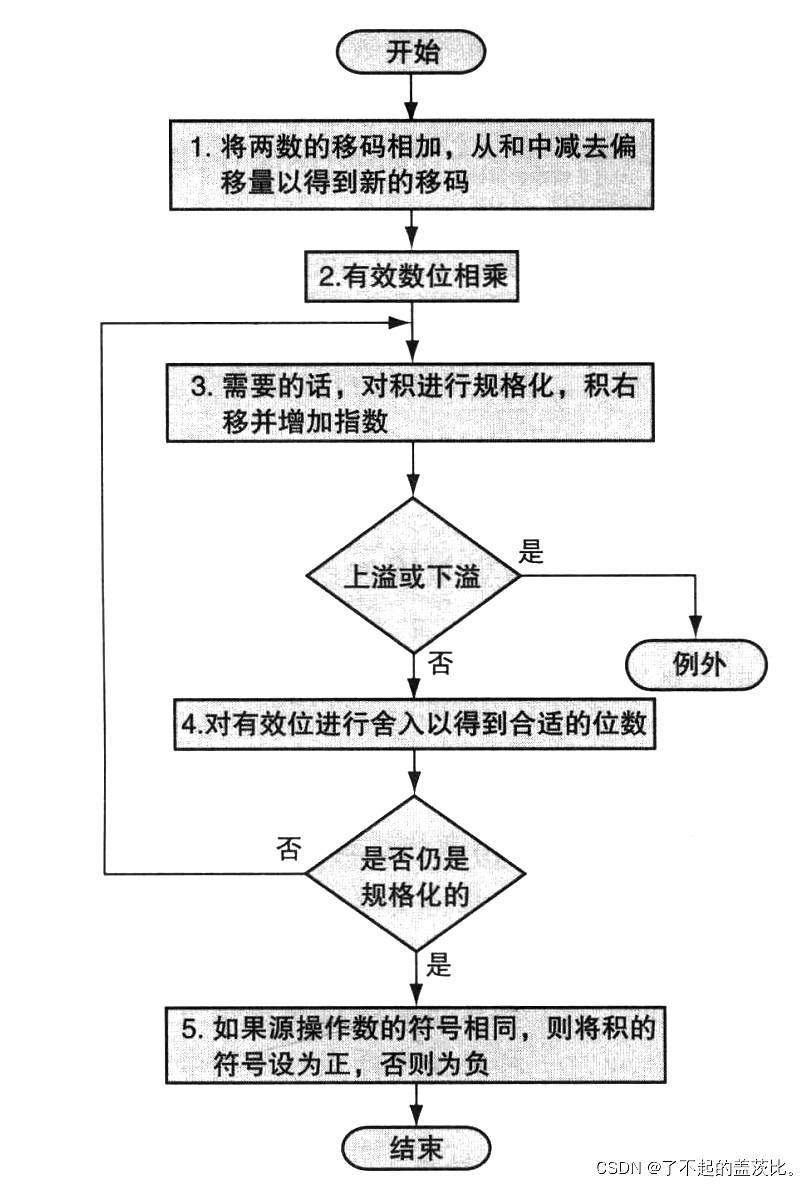
在这里插入图片描述

2.4 浮点加法

浮点加法的核心是“对齐指数”——使两个数的指数相同，再对尾数进行加法运算，具体步骤如下（以十进制科学记数法为例，假设有效数字保留 4 位，指数保留 2 位）：

示例：计算 $9.999 \times 10^1 + 1.610 \times 10^{-1}$

步骤 1：对齐指数
选择指数较大的数（ $9.999 \times 10^1$ ，指数为 1），将指数较小的数（ $1.610 \times 10^{-1}$ ）的尾数右移，使指数变为 1：
$1.610 \times 10^{-1} = 0.1610 \times 10^0 = 0.01610 \times 10^1$
因有效数字仅保留 4 位，故调整后为 $0.016 \times 10^1$ （舍去末尾的 10）。
步骤 2：尾数相加
将对齐后的两个数的尾数相加：
$9.999 + 0.016 = 10.015$
此时结果为 $10.015 \times 10^1$ 。
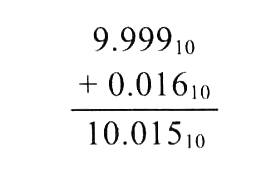
步骤 3：规格化结果
上述结果不符合规格化要求（小数点左侧需仅 1 个非零数字），需调整指数并移位尾数：
$10.015 \times 10^1 = 1.0015 \times 10^2$
此时需检测指数是否溢出（ $2$ 在 2 位指数的表示范围内，无溢出）。
步骤 4：舍入尾数
因有效数字仅保留 4 位，对 $1.0015$ 舍入（四舍五入），结果为 $1.002 \times 10^2$ 。

二进制浮点加法示例（计算 $0.5_{10} + (-0.4375_{10})$ ）

转换为规格化二进制：
$0.5_{10} = 1.000 \times 2^{-1}$ （单精度，4 位有效数字）；
$-0.4375_{10} = -0.0111_2 = -1.110 \times 2^{-2}$ （规格化后）。
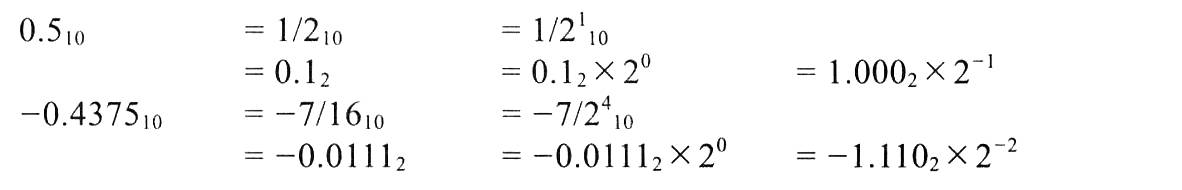
对齐指数：
指数较大的为 $- 1$ ，将 $−1.110 \times 2^{-2}$ 的尾数右移 1 位，指数变为 $- 1$ ：
$−1.110 \times 2^{-2} = -0.1110 \times 2^{-1}$ （保留 4 位有效数字，为 $−0.111 \times 2^{-1}$ ）。
尾数相加：
$1.000 + (- 0.111) = 0.881$ （二进制为 $0.1101_2$ ），结果为 $0.1101 \times 2^{-1}$ 。
规格化与舍入：
结果已规格化（ $0.1101 \times 2^{-1} = 1.101 \times 2^{-2}$ ），有效数字为 4 位，无需舍入，最终结果为 $1.101 \times 2^{-2}$ （十进制为 $0.0625$ ，与手工计算一致）。

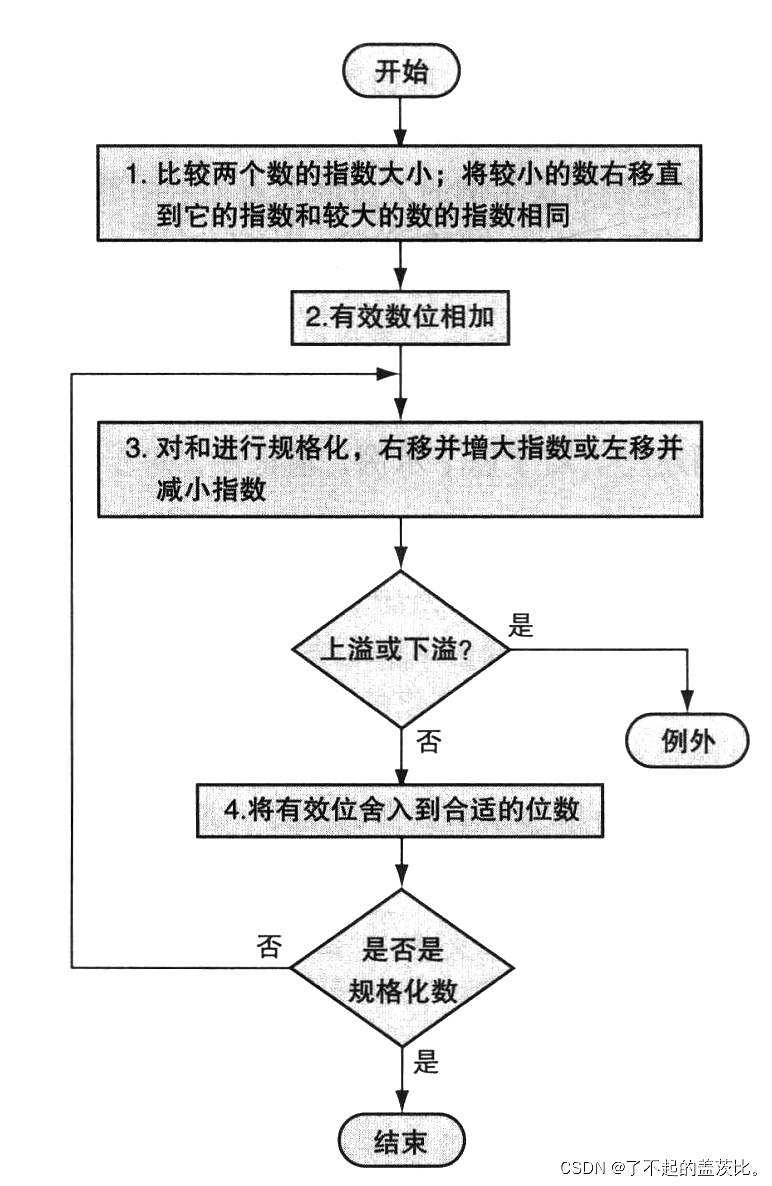
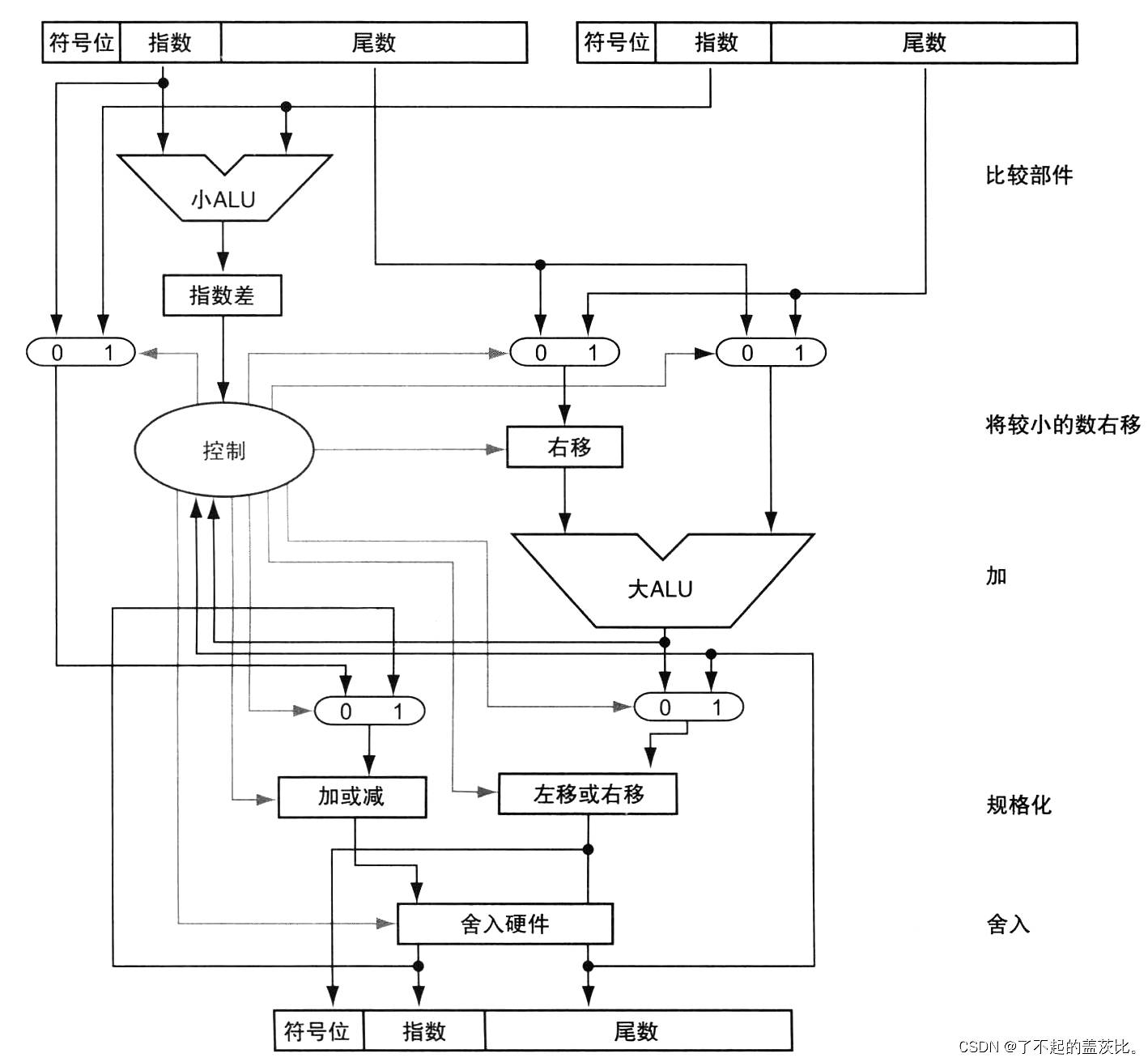
在这里插入图片描述

2.5 浮点乘法

浮点乘法的核心是“指数相加、尾数相乘”，无需对齐指数，具体步骤如下（以十进制科学记数法为例）：

示例：计算 $1.1110 \times 10^{10} \times 9.200 \times 10^{-5}$

步骤 1：计算指数
实际指数相加： $10 + (- 5) = 5$ ；
若用偏移表示（单精度，偏移值 127）：
存储指数 1 = $10 + 127 = 137$ ，存储指数 2 = $- 5 + 127 = 122$ ；
相加后需减去偏移值（避免重复偏移）： $137 + 122 - 127 = 132$ （对应实际指数 $132 - 127 = 5$ ）。
步骤 2：计算尾数
将两个数的尾数相乘： $1.1110 \times 9.200 = 10.2112$ ；
此时结果为 $10.2112 \times 10^5$ 。
步骤 3：规格化结果
调整为规格化形式： $10.2112 \times 10^5 = 1.02112 \times 10^6$ ；
检测指数（6 在 2 位指数范围内，无溢出）。
步骤 4：舍入尾数
有效数字保留 4 位，对 $1.02112$ 舍入，结果为 $1.021 \times 10^6$ 。
步骤 5：确定符号
两个操作数均为正数（符号位均为 0），故结果符号位为 0，最终结果为 $+1.021 \times 10^6$ 。

在这里插入图片描述

二进制浮点乘法示例（计算 $0.5_{10} \times (-0.4375_{10})$ ）

转换为规格化二进制：
$0.5_{10} = 1.000 \times 2^{-1}$ （单精度，4 位有效数字）；
$-0.4375_{10} = -1.110 \times 2^{-2}$ 。
计算指数
实际指数相加： $- 1 + (- 2) = - 3$ ；
偏移表示（单精度）： $(- 1 + 127) + (- 2 + 127) - 127 = 124$ （对应实际指数 $124 - 127 = - 3$ ）。
计算尾数
尾数相乘： $1.000 \times 1.110 = 1.110000$ （二进制）；
结果为 $1.110000 \times 2^{-3}$ （保留 4 位有效数字，为 $1.110 \times 2^{-3}$ ）。
规格化与舍入
结果已规格化，无溢出，无需舍入。
确定符号
操作数符号相反（一正一负），故结果符号位为 1，最终结果为 $−1.110 \times 2^{-3}$ （十进制为 $- 0.21875$ ，与手工计算一致）。

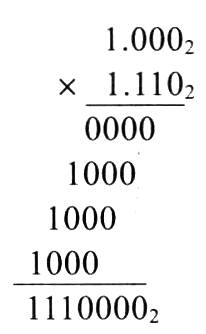
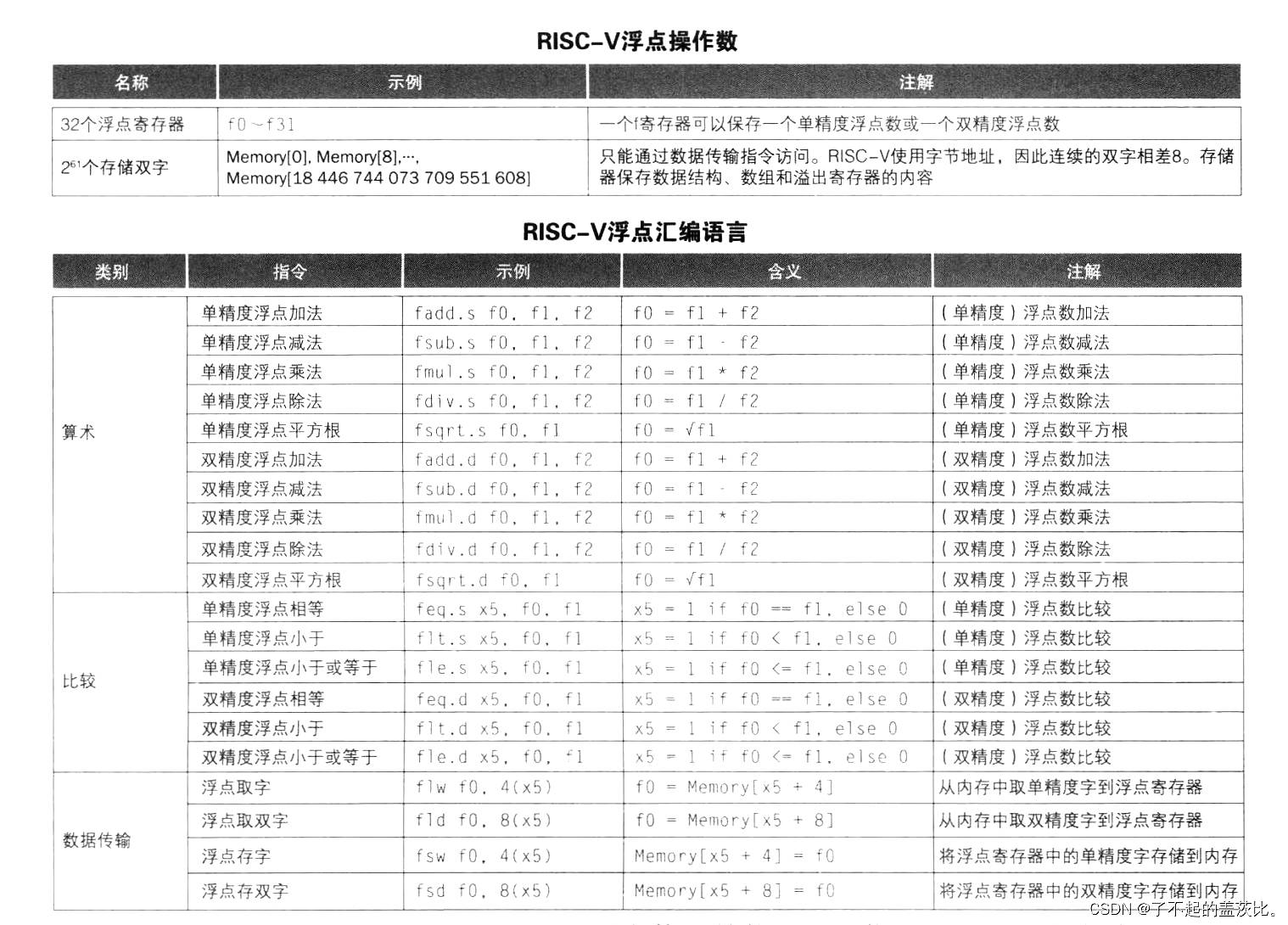
在这里插入图片描述

2.6 RISC-V 中的浮点指令

RISC-V 为浮点运算提供独立的指令集，涵盖加法、减法、乘法、除法、比较等操作，并配备独立的浮点寄存器（f0 ~ f31），具体指令分类如下：

2.6.1 基本运算指令

指令类型	单精度指令	双精度指令	功能描述
加法	`fadd.s`	`fadd.d`	两个浮点数相加
减法	`fsub.s`	`fsub.d`	两个浮点数相减
乘法	`fmul.s`	`fmul.d`	两个浮点数相乘
除法	`fdiv.s`	`fdiv.d`	两个浮点数相除
平方根	`fsqrt.s`	`fsqrt.d`	计算浮点数的平方根

2.6.2 比较指令

指令类型	单精度指令	双精度指令	功能描述
相等比较	`feq.s`	`feq.d`	判断两个浮点数是否相等，结果存入整数寄存器（1 为相等，0 为不相等）
小于比较	`flt.s`	`flt.d`	判断第一个浮点数是否小于第二个，结果存入整数寄存器（1 为是，0 为否）
小于等于比较	`fle.s`	`fle.d`	判断第一个浮点数是否小于等于第二个，结果存入整数寄存器（1 为是，0 为否）

2.6.3 寄存器与数据传输指令

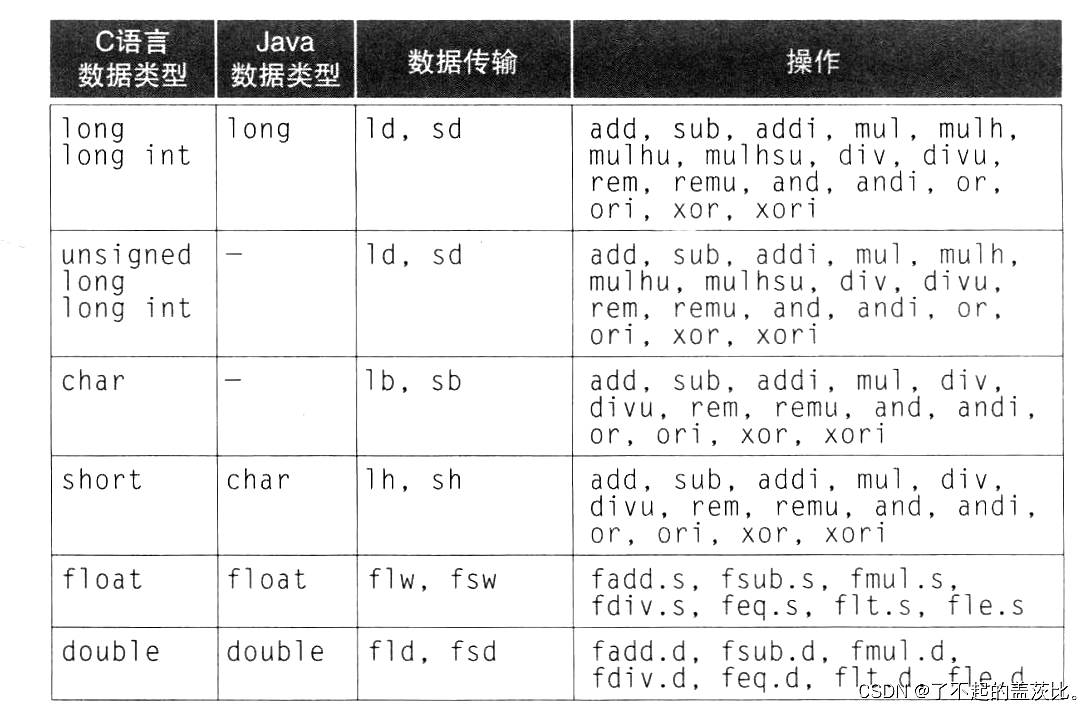
RISC-V 为浮点寄存器设计了独立的数据传输指令，以区分单精度（32 位）和双精度（64 位）数据：

数据类型	指令名称	功能描述
单精度	`flw`	从内存加载单精度浮点数到浮点寄存器
单精度	`fsw`	从浮点寄存器存储单精度浮点数到内存
双精度	`fld`	从内存加载双精度浮点数到浮点寄存器
双精度	`fsd`	从浮点寄存器存储双精度浮点数到内存

需注意：

浮点寄存器 f0 ~ f31 为独立寄存器组，与整数寄存器 x0 ~ x31 无关联；
单精度浮点数仅占用浮点寄存器的低 32 位，双精度浮点数占用完整 64 位；
与整数寄存器 x0 固定为 0 不同，浮点寄存器 f0 无硬件固定值，需通过指令赋值。

在这里插入图片描述

2.7 精确算术与舍入

2.7.1 浮点数的近似性

与整数可精确表示范围内所有数值不同，浮点数仅能精确表示有限个数值（双精度浮点数最多可精确表示 $2^{53}$ 个数值），绝大多数实数需通过“近似值”表示。其根本原因是：任意两个实数之间存在无穷多个实数，而浮点数的字长固定，无法覆盖所有可能值。

为降低近似误差，IEEE 754 标准定义了多种舍入方式，核心目标是使近似值尽可能接近真实值，常用舍入方式为“四舍五入到最近值”（默认方式）。

2.7.2 保护位与舍入位

为提升舍入精度，浮点运算的中间过程会保留额外的“保护位”和“舍入位”：

保护位：中间结果尾数右侧保留的第一位额外位，用于判断尾数的下一位数值；
舍入位：中间结果尾数右侧保留的第二位额外位，辅助保护位进行更精确的舍入判断。

示例：利用保护位与舍入位优化舍入结果

计算 $2.56 \times 10^0 + 2.34 \times 10^2$ ，假设有效数字保留 3 位，分别对比“有保护位/舍入位”与“无保护位/舍入位”的结果差异：

步骤 1：对齐指数
指数较大的数为 $2.34 \times 10^2$ （指数=2），将 $2.56 \times 10^0$ 调整为 $0.0256 \times 10^2$ ；
- 有保护位/舍入位：保留后两位额外位（保护位=5，舍入位=6），记为 $0.0256 \times 10^2$ ；
- 无保护位/舍入位：舍去后两位，记为 $0.02 \times 10^2$ 。
步骤 2：尾数相加
- 有保护位/舍入位： $2.34 + 0.0256 = 2.3656$ ，结果为 $2.3656 \times 10^2$ ；
- 无保护位/舍入位： $2.34 + 0.02 = 2.36$ ，结果为 $2.36 \times 10^2$ 。
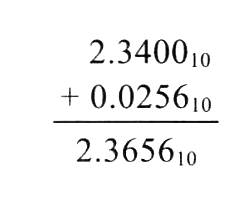
步骤 3：舍入到 3 位有效数字
- 有保护位/舍入位： $2.3656$ 舍入后为 $2.37$ （因舍入位=5，需向高位进 1），最终结果 $2.37 \times 10^2$ ；
- 无保护位/舍入位：结果直接为 $2.36 \times 10^2$ 。

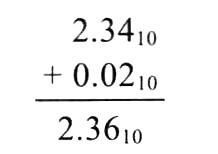
可见，保护位与舍入位可减少舍入误差，使结果更接近真实值（真实值为 $2.56 + 234 = 236.56$ ， $2.37 \times 10^2$ 更接近该值）。

2.7.3 精度衡量指标：ULP

浮点数的精度通常用“最后位置单位”（Unit in the Last Place，ULP）衡量：1 ULP 表示浮点数尾数最低有效位的 1 个单位差值。例如，若一个浮点数的近似值比真实值小 2 个最低有效位，则称其误差为 -2 ULP。在无溢出、下溢或无效操作的情况下，IEEE 754 标准要求浮点数运算结果的误差不超过 0.5 ULP（即“半精度误差”）。

2.8 总结

浮点数的含义需结合其表示规则解读，相同的二进制位在不同浮点格式下可能对应不同数值。IEEE 754 标准为浮点数定义了统一的表示形式：
$(-1)^s \times (1 + F) \times 2^{(E - \text{偏移值})}$
其中 $s$ 为符号位， $F$ 为尾数字段值， $E$ 为指数字段存储值，偏移值在单精度下为 127、双精度下为 1023。

需注意：浮点数通常是实数的近似表示，计算机系统需通过舍入、保护位等机制最小化近似误差；程序设计中需意识到这种近似性可能带来的影响（如精度损失、运算结果偏差等）。

在这里插入图片描述

3. 谬误与陷阱

3.1 谬误：右移指令等同于除以 $2$ 的幂的整数除法

该观点仅对特定情况成立，存在明显局限性：

对于无符号整数和非负带符号整数，右移（逻辑右移）确实等同于除以 $2$ 的幂并向下取整
但对于负的带符号整数（二进制补码表示），算术右移结果与数学除法结果并不总是一致。例如， $- 5$ （二进制 1011）右移 $1$ 位得到 1101（ $- 3$ ），与 $- 5/2$ 向下取整结果一致；但这种一致性基于特定取整规则，并非普遍适用，不能简单等同。

3.2 陷阱：浮点加法满足结合律

数学中的加法满足结合律（ $(a + b) + c = a + (b + c)$ ），但浮点加法因精度限制和舍入误差不满足这一性质：

示例：设 $\times 10^{30}$ ， $\times 10^{30}$ ， $c = 1.0$
- $(a + b) + c = 0.0 + 1.0 = 1.0$
- $\times 10^{30} + (-1.0 \times 10^{30}) = 0.0$
- 两者结果不同，证明浮点加法不满足结合律

这一特性在数值计算中至关重要，不同运算顺序可能导致结果显著差异。

3.3 谬误：浮点数的"相等比较"可直接使用整数相等逻辑

由于浮点数的近似性，两个数学上相等的实数可能因舍入误差表现为不同浮点值；反之，不相等的实数也可能因舍入存储为相同浮点值。直接使用 “==” 判断浮点数相等可能导致错误。

示例：浮点数相等比较的误区

判断 $0.1 + 0.2$ 与 $0.3$ 是否相等：

数学上： $0.1 + 0.2 = 0.3$
浮点表示： $0.1$ 和 $0.2$ 的二进制是无限循环小数，舍入后相加结果约为 $0.30000000000000004$ ，与 $0.3$ 的浮点值（约 $0.29999999999999998$ ）不相等，用 “==” 判断会返回"不相等"，与数学逻辑矛盾。

正确的浮点数相等比较方法

应通过判断两数差值的绝对值是否小于极小阈值（如 $\epsilon = 10^{-9}$ ）实现：
$\epsilon$
其中 $\epsilon$ 需根据精度调整，单精度通常取 $10^{-6}$ ，双精度取 $10^{-9}$ 。

3.4 陷阱：忽略浮点运算的"下溢"影响

浮点下溢指运算结果绝对值小于硬件可表示的最小正数（单精度约 $\times 10^{-38}$ ，双精度约 $\times 10^{-308}$ ），此时硬件通常将结果置为 $0$ （“渐失下溢”）。若程序未考虑下溢，可能因"微小值被当作 $0$ "导致后续计算偏差。

示例：下溢导致的计算错误

物理模拟程序计算分子速度微小变化 $v_0 + \Delta v$ ，其中 $v_0 = 1.0$ （双精度）， $\Delta v = 10^{-310}$ （小于双精度最小可表示正数）：

硬件处理： $\Delta v$ 因下溢被置为 $0$ ，结果 $v = 1.0$
实际影响： $\Delta v$ 虽小，但长期累积（如迭代 $10^{20}$ 次）会显著影响结果，导致模拟偏离真实过程。

规避下溢的方法

选择更高精度格式：如单精度改双精度，或使用扩展精度浮点（如 $80$ 位）
数值缩放：对数值进行缩放（如乘以 $10^k$ ），使微小值脱离下溢范围，计算后再还原
检测下溢状态：通过浮点控制与状态寄存器（如 RISC-V 的 fcsr）检测下溢，触发处理逻辑

3.5 谬误："乘以 $2$ 的幂"的浮点运算可直接用左移指令实现

整数运算中左移 $k$ 位等价于乘以 $2^k$ ，但该逻辑不适用于浮点运算：

表示结构不同：浮点数由符号位、指数字段、尾数字段组成，“乘以 $2^k$ ” 本质是"指数增加 $k$ "，而非"尾数左移 $k$ 位"
规格化约束：尾数左移可能超出 $[1.0, 2.0)$ 范围，需调整指数重新规格化，左移指令无法自动处理
符号位独立：浮点符号位与数值部分分离，左移可能误操作符号位导致错误

正确的浮点"乘以 $2^k$ "实现

应通过修改指数字段实现：

单精度：新存储指数 $E_{\text{new}} = E_{\text{store}} + k$ ，需在 $\leq E_{\text{new}} \leq 255$ 范围内，否则触发溢出
双精度：新存储指数 $E_{\text{new}} = E_{\text{store}} + k$ ，合法范围 $\leq E_{\text{new}} \leq 2047$

部分指令集（如 RISC-V）提供专门的浮点缩放指令（fscale.s/fscale.d），直接实现该功能。

3.6 谬误：整型数据的并行执行策略也适用于浮点数据

整型和浮点型数据运算特性有本质区别，并行策略不能直接通用：

整数运算结果精确，浮点运算存在舍入误差
整数溢出处理与浮点异常（上溢、下溢、 $\text{NaN}$ 等）机制不同
浮点运算延迟通常更长，且不同操作（加、乘、除）延迟差异大
整型位级操作（如掩码、移位）在浮点处理中很少适用

因此，针对整型设计的并行优化策略（如向量化、流水线调度）需根据浮点特性专门设计。

3.7 谬误：只有理论数学家关心浮点精度

浮点精度问题在实际应用中至关重要：

金融计算中，微小误差可能导致显著资金偏差
工程模拟中，误差累积可能使结果与实际严重不符
科学计算中，精度不足可能掩盖重要物理现象或导致错误结论
控制系统中，精度问题可能影响稳定性和可靠性

任何涉及浮点运算的领域都需关注精度，开发者必须了解其特性并采取措施保证结果可靠。

4. 浮点运算的工程实践建议

基于上述谬误与陷阱，浮点运算程序设计需遵循以下建议，以提升精度和可靠性：

4.1 优先选择双精度浮点（double）

单精度浮点尾数字段 $23$ 位（有效数字约 $7$ 位十进制），双精度 $52$ 位（约 $\sim 17$ 位）。精度要求高的场景（科学计算、工程模拟、金融计算）优先使用双精度，可显著减少舍入误差累积。

4.2 合理调整运算顺序，减少误差累积

浮点运算误差具有累积性，运算顺序影响最终误差。通常遵循"先计算小数，再计算大数"原则，避免"大数吞噬小数"（小数与大数相加时有效位被舍入丢失）。

示例：优化运算顺序减少误差

计算 $10^{30} + 1 + 1 + \dots + 1$ （共 $10^6$ 个 $1$ ）：

错误顺序：先算 $10^{30} + 1$ （结果仍为 $10^{30}$ ），再依次加剩余 $1$ ，最终结果 $10^{30}$ （所有 $1$ 被吞噬）
正确顺序：先将 $10^6$ 个 $1$ 相加得 $10^6$ ，再与 $10^{30}$ 相加，结果 $10^{30} + 10^6$ （可被双精度精确表示）

4.3 避免使用浮点类型存储精确数值

浮点数无法精确表示所有十进制小数（如 $0.1, 0.2, 0.3$ 等）。需精确存储的场景（货币金额、整数计数）应改用整数类型（如金额单位从"元"改为"分"）或定点数类型。

4.4 主动检测浮点异常状态

浮点运算可能触发多种异常（上溢、下溢、无效操作、除以零等），部分硬件默认忽略这些异常（如上溢置为 $\infty$ ，下溢置为 $0$ ），但可能导致后续计算错误。程序应主动读取浮点控制与状态寄存器（如 RISC-V 的 fcsr），检测异常并触发处理逻辑（日志告警、程序中断、调整策略）。

RISC-V 的 fcsr 寄存器包含以下异常标志位：

NX（无效操作）：如 $\infty - \infty$
UF（下溢）：结果小于最小可表示正数
OF（上溢）：结果大于最大可表示正数
DZ（除以零）：除数为 $0$ 且被除数非零
NV（舍入误差）：运算结果发生舍入

程序可通过读取这些标志位，及时发现异常，避免错误扩散。

5. 总结

计算机计算功能分为整数运算与浮点运算两大核心：

整数运算：基于二进制补码表示，核心操作是移位与加减，乘法通过"移位-累加"实现，除法通过"减法-移位"实现，需重点关注溢出检测与处理
浮点运算：基于 IEEE 754 标准，通过"符号位-指数字段-尾数字段"表示实数，核心操作需处理指数对齐（加减法）、指数相加（乘法），因近似性需关注舍入误差、异常检测，且需规避"不满足结合律""相等比较陷阱"等问题

工程实践中，需根据场景选择合适数值类型（整数/单精度/双精度），优化运算顺序，主动检测异常，才能确保计算结果的精度与可靠性。后续可进一步学习向量运算、矩阵运算等高级功能，以及硬件加速技术（如 GPU、FPGA 对并行计算的优化），深入理解计算机计算能力的底层支撑。