多元线性回归中的标准化系数与非标准化系数：如何正确解读与应用

多元线性回归是社会科学、经济学、教育学等领域中最常用的统计方法之一。它帮助我们理解多个自变量对一个因变量的影响关系。然而，许多研究者在解读回归结果时，常常对“非标准化系数（B）”和“标准化系数（Beta）”感到困惑：它们究竟代表什么？该如何选择使用？本文将从基本概念出发，结合实际案例与SPSSAU分析结果，系统介绍这两种系数的含义、区别与应用场景，并辅以可视化流程图帮助读者理解分析全过程。

一、什么是非标准化系数与标准化系数？

1. 非标准化系数（B）

非标准化系数，也称为“原始系数”或“B值”，表示自变量每变动一个单位，因变量预期会变动多少单位。例如，在分析“人均教育投入”对“一本上线率”的影响时，非标准化系数为0.034，意味着每增加1千元的教育投入，一本上线率预计提高0.034个百分点。

公式表达：
在回归模型 Y=B0+B1X1+B2X2+...+BkXk+ε中，Bi 即为第i个自变量的非标准化系数。

2. 标准化系数（Beta）

标准化系数是通过将原始数据转换为Z分数（即减去均值后除以标准差）后计算得到的系数。它消除了量纲的影响，使得不同自变量之间的影响程度可以相互比较。例如，Beta值为0.802的变量，其影响力要远高于Beta值为0.003的变量。

公式表达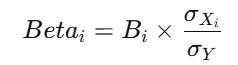：，其中，σXi是自变量 Xi的标准差，σY是因变量Y的标准差。

二、为什么要区分两种系数？

在实际研究中，我们常常面临以下问题：

• 自变量单位不同，无法直接比较影响力大小；
• 希望了解“哪个变量的影响更大”；
• 需要判断模型是否受到多重共线性的干扰。

这时，标准化系数就显示出其价值。它提供了一个“统一尺度”，使我们能够在不同变量之间进行公平比较。而非标准化系数则更适用于实际预测和政策建议，因为它直接反映了变量变动对结果的“实际影响量”。

下面我们通过一个分析流程图来展示多元线性回归的完整分析步骤：

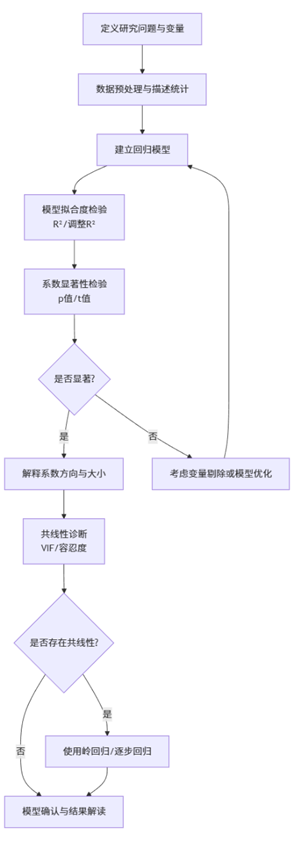
上图展示了多元线性回归的典型分析流程。从问题定义开始，经过数据准备、模型建立、拟合度检验、系数显著性判断，再到共线性诊断与处理，最终完成模型确认与结果解读。这一流程体现了回归分析的系统性与逻辑性，也提示我们在分析中需逐步验证模型的合理性。

三、如何解释标准化与非标准化系数？——以SPSSAU输出为例

让我们通过一个来自SPSSAU的实际研究案例来具体解读这两种系数。这是一项关于人力资源与收入关系的研究，旨在探究多个因素对个人工资水平的影响。

研究模型：
因变量：工资（单位：货币单位）
自变量：年龄、教育年限、工龄、现雇佣年数

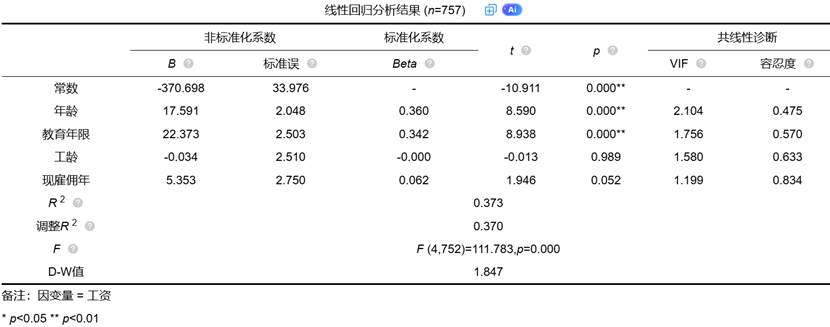
以下是SPSSAU输出的线性回归分析结果：

1. 非标准化系数(B)的实务解读

非标准化系数表示自变量每变化一个单位，因变量预期的实际变化量。

• 常数项(-370.698)：从理论上讲，当所有自变量(年龄、教育年限等)都为0时，工资的预测值为-370.698货币单位。这在现实中显然不合理，提示我们模型在零点附近的预测需要谨慎对待，也可能反映了某些未观测因素的影响。
• 年龄(B=17.591)：在控制其他因素不变的情况下，年龄每增加1岁，工资平均增加17.591货币单位。这是一个实际效应量，对于政策制定和薪酬规划具有直接参考价值。
• 教育年限(B=22.373)：教育年限每增加1年，工资平均增加22.373货币单位。这一系数的经济意义十分明确，为教育投资的回报率提供了量化依据。
• 现雇佣年(B=5.353)：在当前雇主处工作年限每增加1年，工资平均增加5.353货币单位，体现了工作稳定性对收入的积极影响。

2. 标准化系数(Beta)的相对重要性比较

标准化系数消除了量纲影响，允许我们在不同自变量间进行影响力比较。

• 年龄(Beta=0.360)：在所有自变量中标准化系数最高，表明年龄对工资的相对影响力最大。当所有变量都以其标准差为单位变化时，年龄变化一个标准差能够引起工资变化0.360个标准差。
• 教育年限(Beta=0.342)：影响力仅次于年龄，但与年龄非常接近。这说明在教育上投入带来的回报与自然年龄增长带来的薪资增长几乎同等重要。
• 现雇佣年(Beta=0.062)：标准化系数较小，表明其对工资的相对影响较弱。
• 工龄(Beta=-0.000)：接近零的系数表明其对工资几乎没有解释力。

3. 统计显著性与实际意义的结合分析

统计学显著性与系数大小需要结合解读：

• 年龄和教育年限：不仅系数较大(B值)，而且统计显著(p<0.01)，标准化系数也较高。这表明它们对工资既有统计学上的显著影响，也有实质性的重要影响。
• 现雇佣年：虽然标准化系数较小(0.062)，但p=0.052接近显著性边界，提示可能存在微弱效应，值得在更大样本中进一步验证。
• 工龄：系数接近零且p=0.989，表明在控制其他变量后，工龄对工资没有显著影响。这一反直觉的发现可能反映了工龄效应已被年龄和教育年限所解释，或者存在复杂的交互作用。

4. 模型整体评估与共线性诊断

该模型的R²=0.370，意味着这四个自变量共同解释了工资变异的37.0%。虽然不算很高，但在社会科学研究中已属可接受范围。

所有变量的VIF值均小于5(最大为2.104)，远低于常用的阈值10，表明模型不存在严重的多重共线性问题。这增强了系数估计的稳定性和可靠性。

D-W值=1.847接近2，提示残差间不存在显著的自相关性，满足回归模型的独立性假设。

下面通过分析流程图展示本案例的完整解读过程：

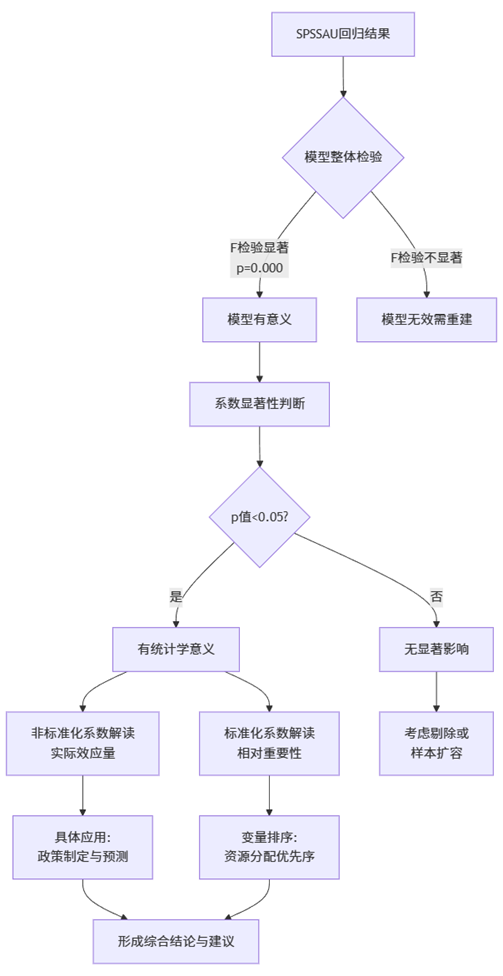
上图展示了回归分析结果的系统解读流程。从模型整体显著性检验开始，到各个系数的统计显著性判断，再分别从非标准化系数（实际效应）和标准化系数（相对重要性）两个维度进行解读，最后结合实务需求形成综合结论。SPSSAU输出的完整结果为此流程提供了所有必要信息，使分析者能够逐步完成从统计结果到实务见解的转换。

总结：如何正确选择与解释系数？

1. 如果你关心实际影响：使用非标准化系数（B）。
2. 如果你关心变量重要性排序：使用标准化系数（Beta）。
3. 永远结合显著性检验与置信区间：无论系数大小，若p值不显著，则不能认为该变量对因变量有可靠影响。
4. 注意共线性干扰：如果VIF值过高，即使系数显著，也可能失真。此时需优化模型或使用正则化方法。

回归分析不仅是一个“跑模型”的过程，更是一个“理解数据”的过程。正确理解标准化与非标准化系数，结合模型检验与诊断，才能做出科学、可信的结论。