多元回归中多重共线性的诊断与处理

在多元回归分析中，自变量之间存在的高度相关性被称为多重共线性。这一问题会导致模型估计不稳定、系数符号异常、显著性检验失真等严重后果。本文将系统阐述多重共线性的诊断方法与处理策略，并结合实际案例展示完整分析流程。

一、多重共线性的本质与影响

多重共线性可分为完全共线性与近似共线性两种类型。完全共线性指自变量间存在精确的线性关系，使得模型无法求解；近似共线性则是更为常见的状况，表现为自变量间高度相关但非完全线性相关。

多重共线性的主要影响体现在：

1. 参数估计值方差增大，估计精度下降
2. 系数对样本数据微小变化敏感，模型稳定性差
3. t检验容易不显著，可能遗漏重要变量
4. 系数符号可能与理论预期相反，难以解释

二、多重共线性的诊断方法体系

规范的多重共线性诊断应当结合多种方法，形成完整的判断体系。其系统化诊断流程如下图所示：

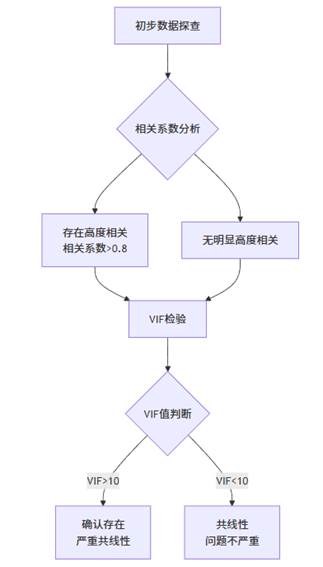
该流程体现了从简单到复杂的递进诊断思路，首先通过相关系数矩阵初步筛查，进而利用方差膨胀因子(VIF)等指标精确量化共线性程度，最终形成综合判断。

1. 简单相关系数矩阵法

计算所有自变量间的Pearson相关系数矩阵，通常认为：

• |r| < 0.3：低度相关
• 0.3 ≤ |r| < 0.8：中度相关
• |r| ≥ 0.8：高度相关，可能存在共线性问题

示例分析：
在一项教育投入对升学率影响的研究中，相关系数矩阵显示：

• 人均教学设备与人均图书的相关系数达0.977
• 人均教学面积与人均教学设备的相关系数为0.933
• 师生比与人均教学面积的相关系数为0.869

这些高度相关的变量对提示存在严重的多重共线性问题。

2. 方差膨胀因子(VIF)与容忍度

VIF是诊断多重共线性的核心指标，计算公式为：

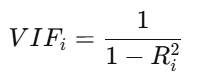
判断标准：

• VIF < 5：共线性不严重
• 5 ≤ VIF < 10：中度共线性
• VIF ≥ 10：严重共线性

容忍度(Tolerance)是VIF的倒数，判断标准为：

• 容忍度 > 0.2：共线性不严重
• 0.1 < 容忍度 ≤ 0.2：中度共线性
• 容忍度 ≤ 0.1：严重共线性

在实际分析中，使用专业工具可以高效完成上述诊断。以SPSSAU为例，其单独提供的【共线性分析】功能能够一键输出所有自变量的VIF值和容忍度，同时提供相关系数矩阵的热力图展示，极大简化了诊断过程。

三、多重共线性的处理方法

当确认存在严重多重共线性时，可采取以下处理策略：

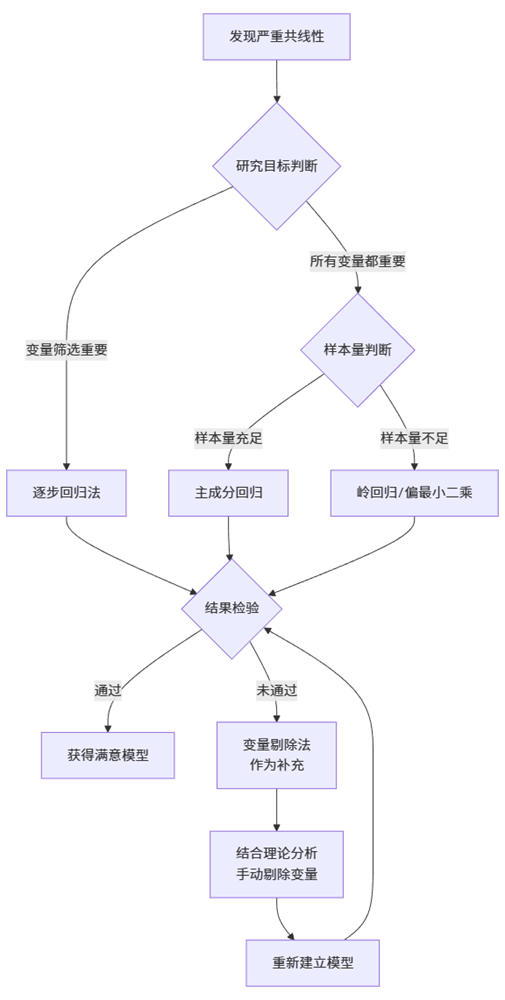
1. 剔除变量法

这是最直接的方法，但需要谨慎操作，避免误删重要变量。

具体实施步骤：

• 计算所有变量的VIF值，从VIF值最大的变量开始考虑剔除
• 每次只剔除一个变量，然后重新计算剩余变量的VIF值
• 结合理论重要性进行判断，优先剔除：
  • 理论意义相对次要的变量
  • 与其他多个变量高度相关的变量
  • 测量精度较低或数据质量较差的变量

注意事项：

• 需要平衡统计指标与理论意义
• 建议记录每次剔除后的模型变化，包括R²、调整R²、AIC等指标的变化
• 最终模型应同时满足统计要求与理论合理性

2. 逐步回归法

通过统计准则自动筛选变量，是较为客观的变量选择方法。

三种主要形式：

• 前向选择：从空模型开始，逐步加入显著性最强的变量
• 后向剔除：从全模型开始，逐步剔除最不显著的变量
• 逐步回归：结合前两种方法，每加入一个新变量后，重新检验已有变量的显著性

判断标准：

• 基于F统计量的显著性水平（通常进入标准p<0.05，剔除标准p>0.10）
• 基于信息准则（AIC、BIC）的最小化原则

优势与局限：

• 优点：自动化程度高，结果相对客观
• 缺点：可能过度依赖统计显著性，忽略理论重要性
• 在SPSSAU中，可以通过勾选相应选项轻松实现逐步回归

3. 主成分回归

通过变量变换彻底消除共线性问题。

实施步骤：

1. 主成分提取：对原始自变量进行主成分分析，提取特征值大于1的主成分
2. 成分选择：选择累计方差贡献率达到85%以上的主成分
3. 建立回归：以主成分得分为新自变量，建立与因变量的回归模型
4. 结果回代：将主成分系数转换回原始变量的系数

优点：

• 完全消除共线性
• 保留绝大部分原始信息
• 适合变量众多且相关性复杂的场景

缺点：

• 结果解释困难，主成分的实际意义不明确
• 转换过程可能丢失部分专业意义

4. 岭回归

通过引入偏误来换取方差的减小，是处理共线性的有效方法。

原理：在最小二乘估计的基础上加入L2正则化项：

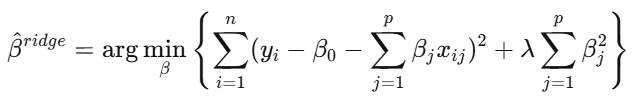
关键技术要点：

• 岭参数选择：通过岭迹图选择稳定的参数估计
  • 观察各系数随k值变化的轨迹
  • 选择系数开始趋于稳定的k值
• 标准化处理：实施岭回归前必须对变量进行标准化
• 交叉验证：使用交叉验证误差最小化原则选择最优岭参数

SPSSAU实现：在【进阶方法】中选择【岭回归】，系统会自动输出不同k值下的系数估计和岭迹图。

5. 偏最小二乘回归

结合主成分分析与多元回归的优点。

特点：

• 同时考虑自变量和因变量的信息
• 特别适合样本量小、变量多的情况
• 通过提取综合变量最大限度地解释因变量的变异

6. 增大样本量

从根本上改善共线性问题的方法。

作用机制：

• 增大样本量可以减小参数估计的方差
• 改善数据矩阵的条件数
• 提供更稳定的估计结果

实践建议：

• 样本量应该是自变量个数的10-20倍以上
• 如果无法增加样本量，考虑减少变量个数

7. 其他创新方法

变量组合：

• 将高度相关的变量组合成综合指标
• 例如：将多个财务指标合并为财务健康指数

有偏估计方法：

• Lasso回归：通过L1正则化同时进行变量选择和参数估计
• 弹性网回归：结合岭回归和Lasso回归的优点

处理效果评估

无论采用哪种方法，都需要对处理效果进行评估：

1. 共线性诊断：处理后的VIF值应小于10，理想情况下小于5
2. 模型拟合优度：调整R²不应显著下降
3. 系数稳定性：不同子样本或不同方法下系数估计应相对稳定
4. 预测能力：模型在测试集上的预测精度应保持合理水平

通过系统性地应用这些方法，研究者可以根据具体研究场景选择最适合的处理策略，确保多元回归分析结果的可靠性和有效性。