面板数据主成分分析小白教程

原创于 2025-12-03 18:13:45 发布 · 367 阅读

CC 4.0 BY-SA版权

文章标签：

在经济管理、社会学、环境科学等众多领域，我们常常会遇到一种经典的数据结构——面板数据。它像一部记录多角色、多时间点的纪录片，既有横截面维度（不同的个体，如省份、企业、个人），又有时间序列维度（不同的时间点）。当我们面对面板数据中多个存在信息重叠的变量，并希望构建一个或多个综合指标时，主成分分析 便成为了一个强有力的工具。

然而，将经典的PCA应用于面板数据，会引发一些独特的挑战与思考。本文将系统地阐述在面板数据中进行PCA的完整流程、核心要点与实操策略，并辅以清晰的图表，助你彻底掌握这一方法。

一、面板数据主成分分析

1. 为什么需要在面板数据上做PCA？

假设你的研究目标是“评估中国各省份的高质量发展水平”。你收集了10年的数据，并选取了GDP增长率、研发投入、污染排放指数、居民幸福度等十几个指标。你立刻会面临两个难题：

维度灾难：十几个指标同时分析，难以刻画一个简洁的综合形象。
共线性困扰：这些指标之间往往相互关联，信息高度重叠，直接用于回归等模型会引发多重共线性问题。

PCA的核心目的就是降维。它通过线性变换，将一组可能存在相关性的原始变量，转换为一组线性不相关的新变量（即主成分）。这些主成分能够最大程度地保留原始数据的信息（方差），同时数量远少于原始变量。

2. 面板数据PCA的特殊性

与单纯的横截面数据不同，面板数据是三维的（N个个体 * T个时间点 * K个变量）。在进行PCA时，我们首先需要将其“压平”，但压平的方式决定了分析的意义。主要有两种思路：

全局PCA：将整个面板数据视为一个大的横截面数据集（样本量为N*T）。这种方法优点是样本量大，结果稳定，能够得到一个统一的、适用于所有时期和个体的综合指标计算框架。这是最常用、最推荐的方法。
截面PCA（逐期PCA）：在每个时间点上，分别对N个个体进行PCA。这种方法适用于研究综合指标的结构随时间变化的场景，但结果在不同时期可能不可比。

本文将重点介绍最普适的全局PCA方法。

二、核心流程

一次完整的、严谨的面板数据PCA分析，可以概括为以下四个关键阶段。其整体流程如下图所示，我们将在后续章节对每一步进行详细拆解。

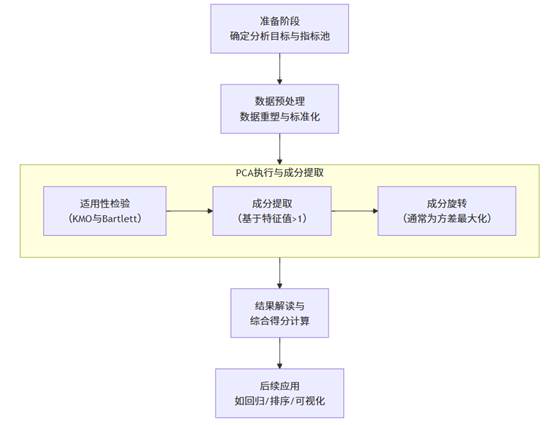
该流程图清晰地展示了从起点到终点的完整分析路径。它始于明确的分析目标，历经严谨的数据准备与检验，核心在于主成分的提取与解读，最终落脚于综合得分的计算与实际应用。这是一个环环相扣的科学过程，任何一步的疏漏都可能导致结果的偏差。

三、分步详解

阶段一：准备与预处理

1.指标正向化

首先，你需要将原始的面板数据整理成一个巨大的二维表格。行是“个体-时间”组合（如“北京-2010", “北京-2011", ... , “上海-2010", ...），列是你的K个原始变量。

紧接着是指标正向化。PCA默认方差越大信息越多，因此所有指标都必须方向一致（通常约定为“越大越好”）。对于逆指标（如污染排放）、适度指标，需要通过取倒数、取绝对值距离等方式进行处理。

2. 数据标准化

这是必不可少的一步。因为原始变量的量纲和数量级通常不同。若直接对原始数据做PCA，方差大的变量（如“GDP”）会“淹没”方差小的变量（如“幸福度得分”），导致主成分几乎由高量纲变量主导。

Z-score标准化是最常用的方法，即将每个变量减去其均值再除以标准差。标准化后的变量均值为0，方差为1，站在了同一起跑线上。在SPSSAU的【数据处理->标准化】模块中，可以一键完成整个数据表的标准化，非常便捷高效。

阶段二：PCA执行与成分提取

本阶段的三个核心步骤构成了PCA的引擎室，其内部运作机制如下图所示。

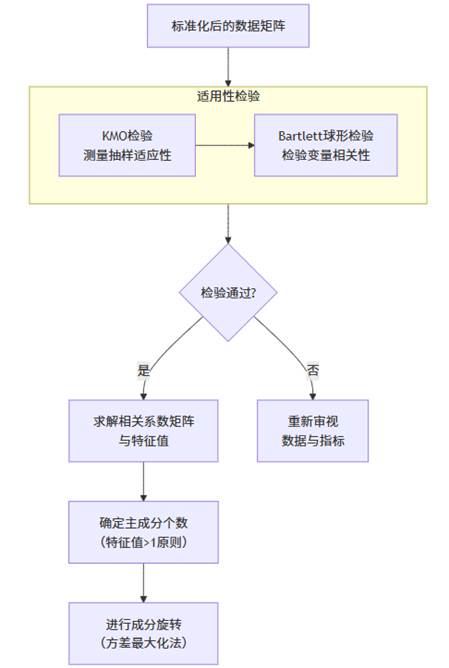
1. 适用性检验

在“动刀”之前，必须先确认数据是否适合做PCA。

KMO检验：用于比较变量间的简单相关和偏相关系数，取值在0-1之间。通常认为KMO > 0.6方可进行PCA，大于0.8则表明非常适合。SPSSAU在输出PCA结果时，会直接给出整体KMO值，方便用户判断。
Bartlett球形检验：用于检验相关系数矩阵是否为单位阵（即变量间彼此独立）。我们希望该检验的p值小于0.05，拒绝原假设，说明变量间存在相关性，适合降维。

2. 成分提取与个数确定

PCA会计算相关系数矩阵的特征值和特征向量。特征值代表了每个主成分所承载的原始信息量（方差）。确定主成分个数的常用准则有：

特征值大于1准则（Kaiser-Guttman准则）：这是最常用、最自动化的准则。保留特征值大于1的主成分。因为标准化后每个变量的方差为1，保留能携带超过1个变量信息的成分是划算的。
碎石检验：绘制特征值从大到小的折线图（碎石图），寻找从“陡峭”到“平缓”的拐点，保留拐点之前的主成分。

在实践中，常将两种方法结合，并由专业软件自动完成。SPSSAU在生成分析结果时，会默认根据特征值大于1输出主成分，并同时提供碎石图以供交叉验证。

3. 成分旋转

为了使提取出的主成分更具解释性，我们通常要进行旋转变换。最常用的是方差最大化旋转。旋转后，每个原始变量在各个主成分上的载荷（相关性）会趋向于0或±1，使得某些变量高度依赖于某个主成分，从而我们可以根据高载荷的变量集合来为这个主成分赋予实际意义（如命名为“经济发展因子”、“环境健康因子”等）。

阶段三：结果解读与综合得分计算

1. 解读成分载荷矩阵

旋转后的成分矩阵是理解主成分内涵的“钥匙”。你需要查看每个原始变量在每个主成分上的载荷值（通常绝对值大于0.5或0.6即认为显著），并根据这些变量集群的共同特征，为主成分命名。

2. 计算综合得分

这是构建最终指标的关键。主成分得分是每个“个体-时间”观测在每个主成分上的坐标值，由原始变量的标准化值加权（载荷）线性组合而成。

如果我们提取了m个主成分，其方差贡献率分别为ω1, ω2, ..., ωm，则综合得分F的计算公式为：
F = (ω1 * F1 + ω2 * F2 + ... + ωm * Fm) / (ω1 + ω2 + ... + ωm)
即以各主成分的方差贡献率为权重，对各个主成分得分进行加权平均。

在SPSSAU中，完成PCA分析后，系统会自动生成主成分得分，并提供一个勾选选项“【综合得分】”，点击后即可自动根据方差贡献率计算并输出最终的综合得分，无需手动计算，极大地简化了工作流程。

四、实战案例：以区域科技创新能力评价为例

假设我们收集了我国30个省份2015-2020年的面板数据，包含R&D经费投入、R&D人员全时当量、专利申请授权数、技术市场成交额四个指标，希望构建一个“区域科技创新综合指数”。

准备与预处理：将数据整理为30*6=180行，4列的结构。所有指标均为正指标，无需正向化。然后进行Z-score标准化。
执行与提取：在SPSSAU的【进阶方法】->【主成分】中，放入四个标准化后的变量。分析得到KMO=0.72，Bartlett检验p<0.001，适合PCA。根据特征值>1准则，提取出1个主成分（特征值为2.8），累计方差贡献率为70.5%。由于只提取了一个成分，无需旋转。
解读与计算：该主成分在四个指标上均有较高载荷（均>0.8），可命名为“科技创新综合因子”。我们直接利用SPSSAU自动计算出的“综合得分”，作为每个省份每年度的科技创新综合指数。
后续应用：此时，原始的4维数据被降维成了1维的“综合指数”。我们可以：
- 进行排名：对不同省份、不同年份的得分进行排序分析。
- 可视化：绘制各省份综合得分随时间变化的趋势图。
- 作为自变量：将此综合得分作为核心解释变量，放入面板回归模型中，研究其对经济增长质量的影响。

五、总结与常见误区

面板数据的PCA是一个将复杂信息凝练为核心洞察的强大过程。它遵循“目标->预处理->检验->提取->解释->应用”的逻辑链。成功的关键在于：

严谨的预处理，特别是标准化。
科学的检验与成分确定，不主观臆断。
清晰的现实解释，让主成分“说人话”。
正确的综合得分计算，确保指标的科学性。

随着分析工具的智能化，像SPSSAU这样的平台已经将PCA中复杂的矩阵计算过程完全封装，面板数据可直接进行主成分分析，面板数据格式相对较为特殊，在分析上直接针对研究指标进行分析即可。