随机前沿分析（SFA）理论与实操：基于SPSSAU的效率测算指南

一、引言：为什么需要测量“效率”？

在经济学、管理学和诸多社会科学领域，我们常常需要评估一个组织（如企业、医院、学校等）的绩效。一个核心的问题是：在给定的资源投入（如劳动力、资本）下，这个组织是否达到了它理论上最大可能的产出？这个“最大可能”与“实际观测”之间的差距，就是效率的体现。

然而，传统的回归方法（如OLS）只能估计平均意义上的投入产出关系，它拟合的是一条“平均生产函数”。这意味着，它默认所有决策单元都处于平均水平，忽略了那些表现卓越或表现不佳的个体。更重要的是，它将所有偏离回归线的部分都归咎于“随机误差”，无法区分这是运气不好（随机冲击）还是自身能力不足（技术无效率）。

为了解决这一问题，随机前沿分析（Stochastic Frontier Analysis, SFA） 应运而生。SFA由Aigner, Lovell & Schmidt (1977) 以及 Meeusen & van den Broeck (1977) 分别独立提出，它巧妙地构建了一个包含两种误差项的模型，从而能够将“技术无效率”从纯粹的“随机噪声”中分离出来，实现对个体技术效率的精准测量。

随着计算方法的发展，像SPSSAU这样的在线统计分析平台，已将复杂的SFA模型封装为易于操作的模块，使研究者无需编程也能进行专业的效率评估。本文将系统梳理SFA的理论基础、核心概念与解读流程，并以SPSSAU的输出逻辑为例，为大家提供一份从理论到实践的全方位指南。

二、SFA核心思想与基本流程

随机前沿分析的核心在于其模型的复合误差项。与传统模型只有一个随机误差项不同，SFA的模型设定如下：

产出 = f(投入) + 随机误差项 (v) - 技术无效率项 (u)

其中：

• f(投入) 是生产函数或成本函数，定义了理论的“前沿面”。
• 随机误差项 (v)：代表各种随机因素，如运气、天气、测量误差等，服从对称的正态分布，可正可负。
• 技术无效率项 (u)：代表由于管理不善、技术落后等因素导致的效率损失，它是一个非负的随机变量，通常服从半正态分布或截断正态分布。正是这个“-u”确保了实际观测值只能位于前沿面之下（对于生产函数）或之上（对于成本函数）。

下图清晰地展示了一个完整的SFA分析流程：

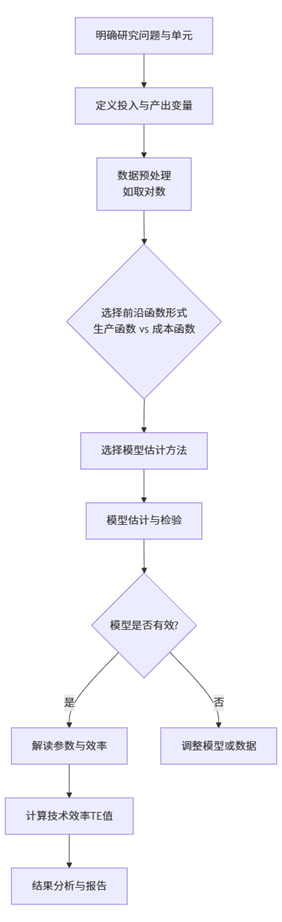
该流程始于清晰的理论框架构建，终于对效率值的深入解读。在整个过程中，SPSSAU提供了从数据准备、模型估计到结果输出的“一站式”解决方案，极大简化了研究者的工作。

三、模型设定：函数形式与估计方法

3.1 生产函数与成本函数

SFA模型首先需要确定函数形式，这取决于研究目标：

• 生产函数（Production Function）：研究在给定投入下，如何实现产出最大化。这是最常用的形式，适用于衡量企业的生产能力。此时，技术无效率使得实际产出低于最大可能产出。
• 成本函数（Cost Function）：研究在给定产出下，如何实现成本最小化。适用于衡量银行、医院等机构的成本控制能力。此时，技术无效率使得实际成本高于最小可能成本。

在SPSSAU中，用户可以根据研究目的直接选择相应的函数类型。

3.2 数据取对数处理

在实证分析中，为了满足模型线性化和缓解异方差性的要求，通常会对投入和产出数据取自然对数。取对数后的线性生产函数（如C-D生产函数）形式为：

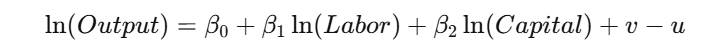
此时，回归系数 ββ 可以解释为产出弹性，即投入增加1%所带来的产出百分比变化。SPSSAU默认提供X和Y均取对数的选项，并能自动处理原始数据中非正数的情况，进行非负平移，确保了分析的可行性。

3.3 估计方法

SFA模型通常采用条件均值法。SPSSAU提供了多种估计方法选项，如条件均值法、均方误差最小化法、条件众数法。对于大多数应用而言，默认的估计方法已能提供稳健的结果，研究者也可以尝试不同方法以对比模型的稳定性。SPSSAU操作示例如下：

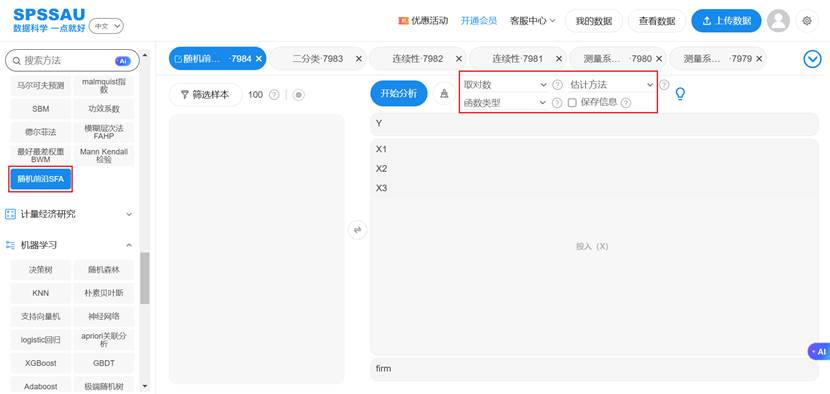
四、模型检验：从整体有效性到参数意义

4.1 似然比检验（Likelihood Ratio Test）

在模型估计后，首要问题是判断模型是否有效。这通过似然比检验（LRT） 来完成。该检验的原假设（H₀）是：“仅包含截距项的模型”与“包含所有投入变量的完整模型”没有显著差异。

• 检验统计量：LR统计量 = -2 × [仅截距模型的对数似然值 - 完整模型的对数似然值]，它近似服从卡方分布。
• 如何判断：如果检验的*p*值小于0.05，则拒绝原假设，表明引入的投入变量共同对产出有显著解释力，模型构建是有效的。
• 信息准则：AIC（赤池信息准则）和BIC（贝叶斯信息准则）用于模型比较，其值越小表示模型拟合越好且更简洁。在进行不同模型设定（如改变函数形式或分布假设）时，这两个指标是重要的评判依据。

4.2 参数估计与解读

参数估计表是SFA分析的核心输出，它提供了以下关键信息：

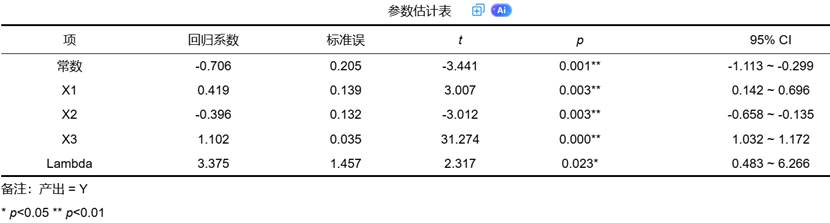
• 常数项：代表了所有投入取值为0（取对数后则为1单位）时，产出的“基准”对数水平，其经济学意义取决于具体的函数形式。
• 投入变量的回归系数：反映了各投入对产出的边际贡献。与OLS回归类似，我们关注其系数符号、大小和显著性（*p*值）。显著的系数意味着该投入对产出有稳定的影响。
• Lambda (λ) 参数：这是SFA模型特有的、至关重要的一个参数。其定义为λ=σu​/σv​，即技术无效率项的标准差与随机误差项标准差的比值。

• λ的显著性：如果λ的*p*值显著（如<0.05），则说明模型中确实存在不可忽略的技术无效率。如果不显著，则意味着技术无效率项不重要，使用SFA模型可能没有必要，传统的OLS或许更合适。
• λ的大小：λ值越大，表明技术无效率项（σ_u）相对于随机误差项（σ_v）在总体误差中占主导地位。换言之，产出与前沿面的差距主要源于管理、技术等内在因素，而非随机运气。

五、方差参数与技术效率（TE）

5.1 方差分解

SFA模型将总误差方差（σ²）分解为两个独立的部分：

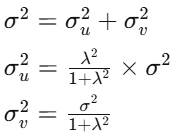
• σ²：总误差方差，衡量了观测值与前沿面预测值的总离散程度。
• σ_u²：技术无效率方差，反映了不同决策单元之间效率差异的波动情况。该值越大，说明各单位效率水平参差不齐。
• σ_v²：随机误差方差，反映了外部随机冲击的波动大小。

5.2 技术效率（Technical Efficiency, TE）的计算与解读

SFA的最终目标之一是计算每个决策单元（如每家企业）的技术效率值。

• 定义：技术效率（TE）是指在给定投入组合下，实际产出与随机前沿面上最大可能产出的比率。即 
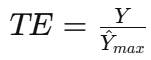
• 取值范围：TE值严格介于0和1之间。
  • TE = 1：表示该单元处于效率前沿，是完全有效率的。
  • TE < 1：表示存在技术无效率。例如，TE=0.8意味着该企业只达到了在同样投入和运气下最优企业产出的80%，有20%的产出潜力因技术无效率而损失。
• 排名与应用：研究者可以根据TE值对所有决策单元进行排名，识别出效率标杆和效率低下的单元，为资源分配和管理改进提供定量依据。

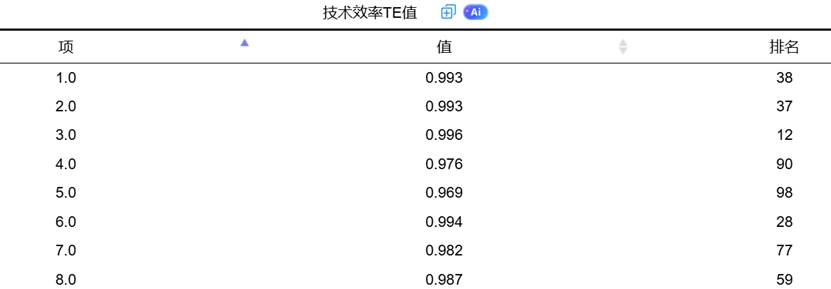
在SPSSAU的分析结果中，会提供一个详尽的技术效率值表格，包含每个样本的TE值及其排名，并给出描述性统计（平均值、中位数、最小值、最大值、标准差），方便研究者从整体上把握样本的效率分布情况。

六、SPSSAU在SFA分析中的实践优势

SPSSAU的随机前沿分析（SFA）模块，将上述复杂的理论模型和计算过程封装成一个用户友好的界面操作，其优势体现在：

• 流程化引导：从变量设置、函数选择到结果输出，逻辑清晰，步步为营。
• 自动化处理：自动完成对数变换、模型估计、似然比检验、效率值计算等所有计算步骤。
• 全面结果输出：提供从基本参数、模型检验、参数估计、方差分解到技术效率排名的完整报告链。
• 可视化与数据导出：支持将技术效率等结果保存至数据平台，便于后续深入分析和可视化呈现。

这使得研究人员，即使是那些不精通极大似然估计编程的学者，也能够轻松、准确地进行前沿的效率分析研究。

七、结论

随机前沿分析（SFA）为我们打开了一扇精确测量效率的大门。它通过独特的复合误差项设定，成功地将随机冲击与技术无效率分离开来，提供了比传统方法更丰富、更深刻的洞察。理解和正确解读SFA的各个环节——从模型设定、似然比检验、参数估计（特别是Lambda值）到最终的技术效率值——是得出可靠研究结论的关键。

通过像SPSSAU这样的现代化统计工具，SFA这一强大而复杂的方法论得以“飞入寻常百姓家”，极大地促进了效率评估研究在各类领域的应用和普及。掌握SFA，意味着你掌握了一把评估组织绩效、挖掘改进潜力的金钥匙。