【深度学习基础】互相关与卷积的本质区别及在深度学习中的应用

​ 在卷积神经网络（CNN）中，我们经常使用卷积操作来提取图像特征。但严格来说，深度学习框架中实际执行的往往是互相关操作。本文将详细剖析互相关和卷积的数学本质与区别，并说明为什么在深度学习中这两者几乎可以互换。

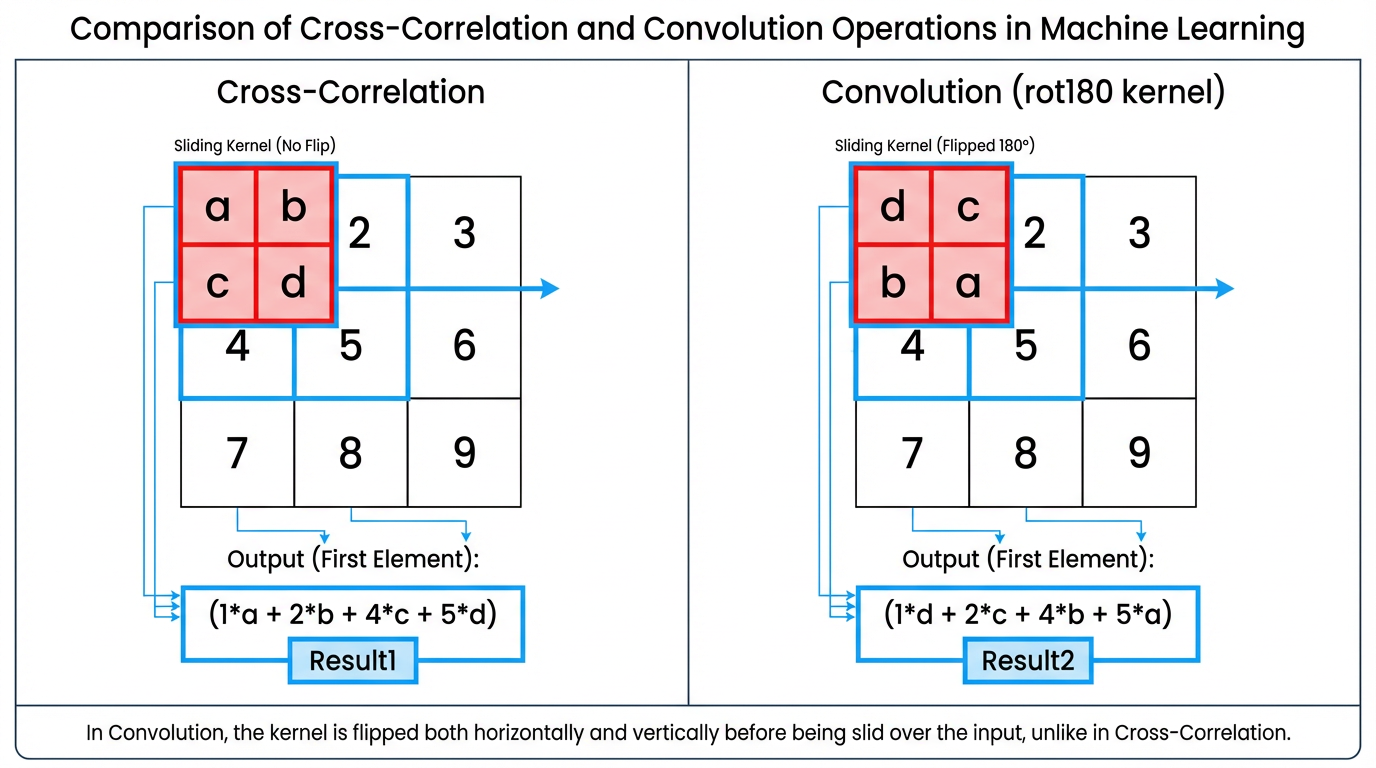
一、 互相关（Cross-correlation）

​ 互相关是一种在两个信号之间寻找相似性的操作。

​ 对于图像而言，可以理解为：将一个卷积核（filter）在图像上滑动，并在每个局部区域与卷积核做点积，提取特征。

1.1 二维互相关公式

​ 给定图像输入 $\mathbf{X}\in {\mathbb{R}}^{M\times N}$，卷积核 $\mathbf{W}\in {\mathbb{R}}^{U\times V}$，互相关运算定义为：
$$y_{ij}=\sum _{u=1}^U\sum _{v=1}^V{w}_{uv}\cdot x_{i+u-1,j+v-1}$$
​ 其中，$y_{ij}$ 表示输出特征图在位置 $(i,j)$ 的值。

1.2 示例

​ 假设输入数组为：
$$\mathbf{X}=\left[\begin{array}{ccc}0& 1& 2\\ 3& 4& 5\\ 6& 7& 8\end{array}\right],\mathbf{W}=\left[\begin{array}{cc}0& 1\\ 2& 3\end{array}\right]$$
​ 互相关第一个输出元素计算如下：
$$0\times 0+1\times 1+3\times 2+4\times 3=19$$
​ 在互相关运算过程中，卷积窗口从输入数组的左上方开始，按从左往右、从上到下的顺序滑动，每次滑动都会将窗口中的输入子数组与核数组按元素相乘再求和，得到输出数组中相应位置的元素。依次计算每个位置的输出，得到完整的输出矩阵。

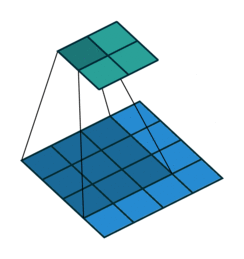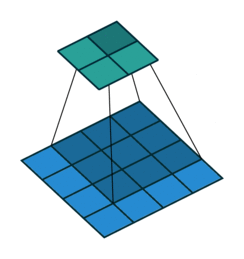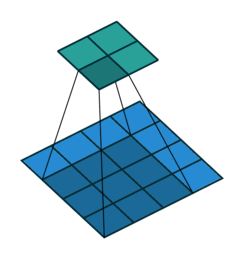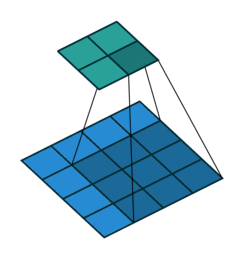
二、卷积（Convolution）

​ 卷积与互相关的公式几乎一样，但有一个关键区别：卷积会在滑动之前将卷积核进行水平和垂直翻转。

• 数学表示为：

$$y_{ij}=\sum _{u=1}^U\sum _{v=1}^V{w}_{uv}\cdot x_{i-u+1,j-v+1}$$

​ 当卷积核旋转180°时，原本位于左上角的元素 $w_{11}$ 会对应输入局部区域的右下角元素 $x_{i-1+1,j-1+1}=x_{i,j}$。

​ 或者更直观地表示为：
$$\mathbf{Y}=\mathbf{W}\ast \mathbf{X}=\text{rot180}(\mathbf{W})\otimes \mathbf{X}$$
​ 其中，rot180(W) 表示将卷积核旋转180度。

三、互相关与卷积的关系

特性	互相关	卷积
核是否翻转	否	是（水平+垂直）
计算方式	滑动窗口逐元素相乘求和	滑动窗口逐元素相乘求和（核先翻转）
特征提取能力	不受翻转影响	不受翻转影响
深度学习中使用	实际使用	常用名称

注意：在深度学习中，大多数框架（如 PyTorch、TensorFlow）执行的实际上是互相关，但为了历史和习惯仍称为“卷积”。核是否翻转并不影响特征提取能力。

四、总结

• 互相关：直接在图像上滑动卷积核计算点积，寻找局部相似性。
• 卷积：在滑动前翻转卷积核，公式上与互相关略有不同。
• 深度学习实践：为了方便和统一术语，互相关通常也被称为卷积。
• 关键点：翻不翻转卷积核不影响特征提取效果，只是数学上的约定不同。