【深度学习原理】数值稳定性（一）：为什么深度神经网络如此脆弱

原创已于 2025-12-27 12:28:18 修改 · 618 阅读

CC 4.0 BY-SA版权

文章标签：

于 2025-12-26 11:50:03 首次发布

5 篇文章

订阅专栏

数值稳定性系列文章：
数值稳定性（一）：为什么深度神经网络如此脆弱
 数值稳定性（二）：梯度是如何在深度网络中消失与爆炸的
第三篇还在写。。。

在训练深度神经网络时，你可能遇到过这样的情况：

在实践中，我们常常会把这些问题归因于：

这些解释当然没有错，但它们更多回答的是“如何缓解”，而不是“为什么会发生”。在许多教材和课程中，梯度消失与梯度爆炸往往被当作一种既定的训练现象来介绍，却很少从计算过程本身解释：为什么只要网络一加深，这类问题就几乎不可避免。

久而久之，这些现象被简化为需要记住和规避的经验法则，而不是可以被理解的数值结果。

写下这一系列文章的初衷，是希望从数值计算与传播过程本身出发，重新理解这些问题：

在这里，我们刻意避免一开始就抛出复杂公式，而是先建立直觉： 不是技巧先行，而是理解先行；不是记结论，而是看清原因。

在这一篇中，我们将回答三个最基础的问题：

这是整个系列的概念基础篇。在后续文章中，我们将逐步把这些直觉形式化，从梯度传播、Jacobian 连乘到工程中的稳定性设计，一步步展开。

从计算的角度看，一个算法是数值稳定的，意味着：在存在浮点误差、近似计算和有限精度的情况下，计算结果不会出现不可控的放大或缩小。

对应地，数值不稳定指的是：

在传统数值计算中，数值稳定性通常通过算法设计来保证；而在深度学习中，这个问题会以一种更“隐蔽但更剧烈”的形式出现。

在神经网络训练过程中，数值不稳定通常不会直接以“报错”的形式出现，而是表现为一系列训练异常现象：

梯度变为 inf 或 NaN
梯度被截断为 0，参数不再更新
loss 曲线剧烈震荡，无法收敛

需要强调的是，这些现象并不是优化算法本身的问题，而是底层数值计算已经失去了稳定性。换句话说，此时优化算法仍在“按规则工作”，但传递给它的数值已经不再可靠。

要理解这一点，需要暂时跳出“模型结构”的视角，从计算过程本身来观察深度神经网络。

如果暂时不从“特征表示”或“语义建模”的角度看问题，而是只关注数值计算本身，深度神经网络的计算过程其实非常单一。

无论是前向传播还是反向传播，深度神经网络都在反复执行两类操作：
- 线性变换（加权求和）
- 非线性变换（激活函数）
当网络变深时，这些操作并不是简单地“多做几次”，而是被一层一层地连续叠加。
从数值的角度看，这意味着：
- 在前向传播中，一个很小的数值偏差，可能在多层计算中被逐步放大或压缩；
- 在反向传播中，梯度需要经过多层计算才能传递到前面的参数，其数值尺度也会在传递过程中不断变化。

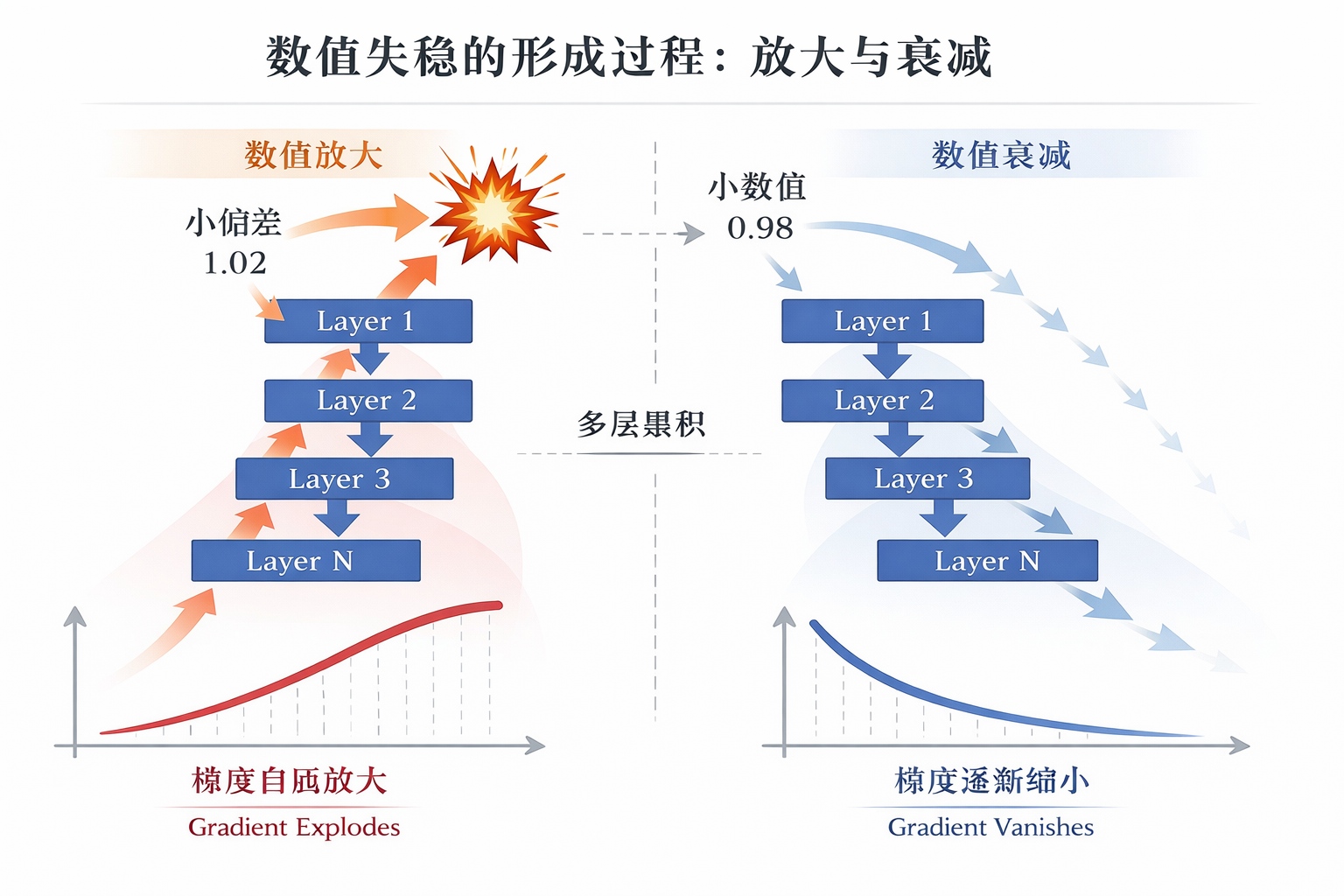
在深度神经网络中，数值问题并不是由某一层“突然出错”引起的，而往往来自多层计算效果的持续叠加。

如果某一层的计算对数值具有轻微的放大作用，那么在多层连续作用下，这种放大会被逐步累积，最终可能超出数值可控的范围；反之，如果每一层都在轻微压缩有效数值，那么即使单次影响看似可以忽略，信息也会在层层传递中不断衰减。

从这个角度看，数值不稳定并不是一个“局部异常”，而是连续计算下尺度逐渐偏离合理区间的结果。

在深度神经网络中，这种由连续计算引发的尺度偏移，最直观地体现在反向传播过程中的梯度变化上。

在训练过程中，数值不稳定往往会以两种典型形式出现：
- 梯度爆炸：梯度在层层反向传播中被不断放大，参数更新幅度失控；
- 梯度消失：梯度在传递过程中被不断压缩，逐渐趋近于 0，导致浅层网络的参数几乎无法更新。
它们看似是两个相反的问题，但本质上来源于同一个原因：数值在多层计算中失去了“合适的尺度”。