【深度学习原理】深入理解梯度爆炸（Gradient Explosion）及解决方案

​ 在深度学习中， 梯度爆炸（Gradient Explosion） 是训练深层神经网络时经常遇到的问题之一。本文将结合数学原理和实践示例，为你全面解析梯度爆炸的原因、现象以及应对策略。

一、梯度爆炸的概念

本节从数学形式出发，解释梯度爆炸是什么、从哪里来、为什么会发生。

​ 在深度学习训练中，梯度爆炸（Gradient Explosion） 指的是反向传播过程中，梯度值快速增大，超过数值类型所能表示的范围，导致模型训练不稳定或直接发散。梯度爆炸是与 梯度消失（Gradient Vanishing） 相对的现象，两者都是深层神经网络训练中常见的数值问题。

1. 梯度爆炸是如何出现的

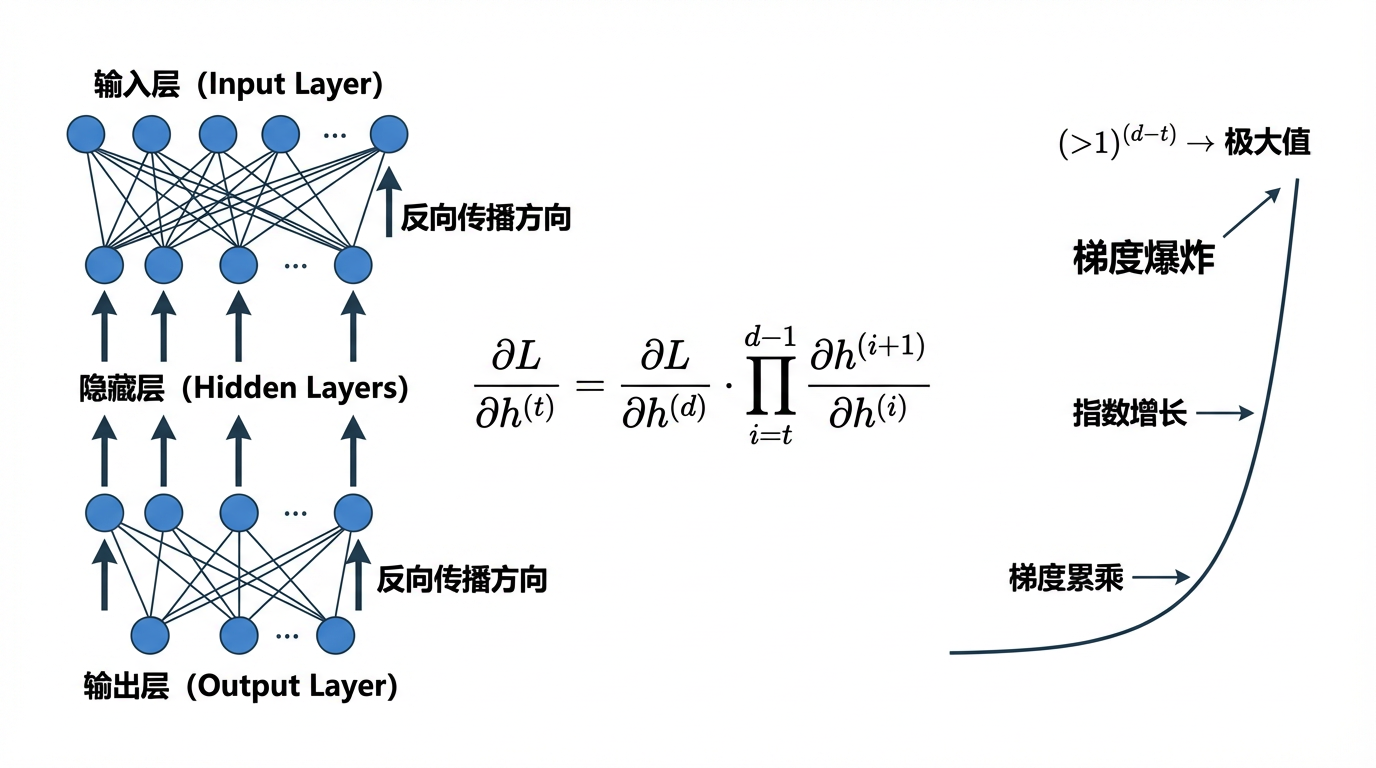
​ 假设我们有一个深度神经网络，反向传播时梯度涉及多层的链式乘积：
$$\frac{\partial L}{\partial {\mathbf{h}}^{(t)}}=\frac{\partial L}{\partial {\mathbf{h}}^{(d)}}\prod _{i=t}^{d-1}\frac{\partial {\mathbf{h}}^{(i+1)}}{\partial {\mathbf{h}}^{(i)}}$$
​ 其中，${\mathbf{h}}^{(t)}$是第$t$层的隐藏状态（或特征表示），$L$是网络的损失函数，$\frac{\partial L}{\partial {\mathbf{h}}^{(t)}}$是损失对第$t$层输出的梯度，${\prod }_{i=t}^{d-1}\frac{\partial {\mathbf{h}}^{(i+1)}}{\partial {\mathbf{h}}^{(i)}}$是从第 $t$层到第$d$层的梯度链式乘积，即链式法则的应用。

​ 简单来说，损失对当前层的梯度 = 后面所有层的梯度“累乘”回来。

• 当网络层数$d-t$很大时，如果每层梯度或权重大于 1，这个乘积就会呈指数增长。
• 这意味着在深层网络中，即使单层梯度不大，累积效果也可能导致最终梯度数值极大。

(1) 链式乘积的来源

• 在深度网络中，每一层输出依赖于前一层：
  $${\mathbf{h}}^{(i+1)}=f({\mathbf{W}}^{(i)}{\mathbf{h}}^{(i)}+{\mathbf{b}}^{(i)})$$

• 反向传播时，损失对 ${\mathbf{h}}^{(i)}$的梯度通过链式法则传递：
  $$\frac{\partial L}{\partial {\mathbf{h}}^{(i)}}=\frac{\partial L}{\partial {\mathbf{h}}^{(i+1)}}\frac{\partial {\mathbf{h}}^{(i+1)}}{\partial {\mathbf{h}}^{(i)}}$$

• 递归展开到第$t$层，就得到公式中的乘积形式。

(2) 为什么会导致梯度爆炸

​ 假设每层梯度或权重矩阵的范数$\frac{\partial {\mathbf{h}}^{(i+1)}}{\partial {\mathbf{h}}^{(i)}}\Vert >1$，那么：
$$\prod _{i=t}^{d-1}\frac{\partial {\mathbf{h}}^{(i+1)}}{\partial {\mathbf{h}}^{(i)}}\sim (\text{大于1}{)}^{d-t}$$

• 当网络层数$d-t$很大时，这个乘积会指数增长，最终导致$\frac{\partial L}{\partial {\mathbf{h}}^{(t)}}$ 极大，从而出现梯度爆炸。

• 反之，如果每层梯度小于 1，就可能出现梯度消失。

2. 对应激活函数的影响(以 ReLU 为例)

上一节从整体链式法则的角度解释了梯度爆炸的来源，下面我们进一步从单层局部梯度的角度，分析激活函数是如何参与梯度放大过程的。

​ 在分析梯度爆炸问题时，激活函数的导数形式会直接影响反向传播过程中梯度的放大或抑制方式。这里以 ReLU 激活函数为例进行说明。

(1) ReLU激活函数的定义

​ ReLU（Rectified Linear Unit）的定义如下：
$$\sigma (x)=\max (0,x)$$
​ 其导数为：
$${\sigma }^{\prime }(x)=\{\begin{array}{ll}1& \text{ if }x>0\\ 0& \text{ otherwise }\end{array}$$

​ 这意味着：

• 当神经元被激活（$x>0$）时，梯度可以无衰减地通过；
• 当神经元未激活（$x\le 0$）时，梯度被完全阻断。

(2) 反向传播中的梯度累乘形式

​ 考虑一个深度前馈网络，在反向传播过程中，从第$t$层到第$d$层的梯度传播可以写成：
$$\frac{\partial {\mathbf{h}}^{(d)}}{\partial {\mathbf{h}}^{(t)}}=\prod _{i=t}^{d-1}\frac{\partial {\mathbf{h}}^{(i+1)}}{\partial {\mathbf{h}}^{(i)}}$$
​ 该公式来源于链式法则，表示梯度在反向传播时需要逐层“传回”，并在每一层都会与该层的局部梯度相乘。网络层数越深，这种累乘效应就越显著。

• 对于使用 ReLU 激活函数的网络，第$i$层的前向传播形式为：
  $${\mathbf{h}}^{(i+1)}=\sigma ({\mathbf{W}}^{(i)}{\mathbf{h}}^{(i)}+{\mathbf{b}}^{(i)})$$

• 忽略偏置项（不影响梯度传播结构），可以利用链式法则将局部梯度展开为：
  $$\frac{\partial {\mathbf{h}}^{(i+1)}}{\partial {\mathbf{h}}^{(i)}}=\text{diag}({\sigma }^{\prime }({\mathbf{W}}^{(i)}{\mathbf{h}}^{(i)})){\mathbf{W}}^{(i)}$$
  其中：

  • $\mathrm{diag}({\sigma }^{\prime }(\cdot ))$是一个对角矩阵，用于表示 ReLU 在每个神经元上的导数
  • 对角线上元素为 1 表示该神经元处于激活状态，梯度可以通过
  • 对角线上元素为 0 表示该神经元未激活，梯度在此被直接阻断
  • ${\mathbf{W}}^{(i)}$则决定了梯度在该层的线性映射和尺度变化。

• 因此，从第$t$层到第$d$层的整体梯度传播形式可以写为：
  $$\prod _{i=t}^{d-1}\text{diag}({\sigma }^{\prime }({\mathbf{W}}^{(i)}{\mathbf{h}}^{(i)})){\mathbf{W}}^{(i)}$$

(3) ReLU对梯度放大的影响

​ 由于 ReLU 的导数${\sigma }^{\prime }(x)$ 只取 0 或 1，这带来两个重要影响：

• 梯度路径筛选（masking）

  • 为 0 的位置直接切断梯度；
  • 为 1 的位置，梯度完全由权重矩阵${\mathbf{W}}^{(i)}$决定。

• 梯度规模主要由权重决定

  在激活为正的路径上，梯度的大小近似来源于：
  $$\prod _{i=t}^{d-1}{\mathbf{W}}^{(i)}$$
  当网络较深（即$d-t$很大），且权重矩阵的谱范数或典型值大于 1 时，梯度会呈指数级增长。

  例如，当网络深度$d-t=100$，权重尺度$\mathbf{W}\approx 1.5$时，则有：
  $$1.5^{100}\approx 4\times 10^{17}$$
  这已经远远超出了数值计算中可控的范围，从而导致梯度爆炸。

3. 矩阵乘积爆炸的直观示例

​ 为了更直观地理解这一现象，可以通过连续矩阵相乘来模拟梯度的累乘过程：

import torch

M = torch.normal(0, 1, size=(4,4))
print('一个矩阵 \n', M)

for i in range(100):
    M = torch.mm(M, torch.normal(0, 1, size=(4, 4)))

print('乘以100个矩阵后\n', M)

​ 示例输出如下：

一个矩阵
tensor([[-2.1385e-01,  4.6225e-01, -5.0861e-01, -8.8057e-01],
        [ 1.4022e+00,  1.0260e+00, -1.2511e+00,  2.2817e-01],
        [-1.0128e+00, -2.6599e-01,  3.2404e-02, -2.2224e+00],
        [-4.3064e-01,  1.3997e-03,  4.1939e-01, -2.0210e-01]])

乘以100个矩阵后
tensor([[-4.3617e+23, -5.9455e+23, -3.7624e+23,  4.6231e+23],
        [-1.7493e+24, -2.3845e+24, -1.5089e+24,  1.8541e+24],
        [ 4.2498e+23,  5.7931e+23,  3.6660e+23, -4.5046e+23],
        [ 5.1668e+23,  7.0431e+23,  4.4570e+23, -5.4765e+23]])

​ 可以看到，即使每个矩阵元素本身来自标准高斯分布，在多次相乘后，结果仍然会迅速膨胀到 $10^{23}$量级以上，这与深层网络中梯度爆炸的行为高度一致。

4. 为什么梯度爆炸会影响训练

​ 梯度爆炸会导致数据溢出、模型参数更新失控、训练过程不稳定等。

(1) 数值溢出（Numerical Overflow）

​ 当梯度在反向传播过程中不断累乘并迅速增大时，其数值可能会超出浮点数的可表示范围。

• 例如：

  • float32 的有效数值范围约为
    $$1.18\times 10^{-38}\sim 3.4\times 10^{38}$$

  • float16 的数值范围更小，在深层网络或混合精度训练中尤为脆弱。

• 一旦梯度或中间激活值超出该范围：数值会被截断为 inf或在后续计算中产生 NaN

  这会直接破坏反向传播过程，使得参数更新失效，训练无法继续。

(2) 模型参数更新失控（Uncontrolled Parameter Updates）

​ 梯度下降的参数更新公式为：
$${\mathbf{W}}_{t+1}\leftarrow {\mathbf{W}}_t-\alpha {\nabla }_{\mathbf{W}}L({\mathbf{W}}_t)$$
​ 其中，$\alpha$是一个标量缩放因子，用于控制沿该方向前进的距离；${\nabla }_{\mathbf{W}}L({\mathbf{W}}_t)$决定更新方向和更新幅度。

• 在参数空间中，一次更新的实际“步长”可以表示为：
  $$\Vert \Delta \mathbf{W}\Vert =\alpha \Vert {\nabla }_{\mathbf{W}}L({\mathbf{W}}_t)\Vert$$

• 当梯度发生爆炸时，即使学习率$\alpha$保持不变，梯度范数$\Vert {\nabla }_{\mathbf{W}}L\Vert$也会急剧增大，从而导致：

  • 单次参数更新幅度异常增大
  • 参数在一次迭代中跳跃到远离当前区域的位置
  • 模型直接偏离原本可能收敛的轨道

  此时，参数更新不再是“沿着损失下降方向的小幅前进”，而更像是一次失控的跳跃，极易导致训练发散。

(3) 训练过程不稳定

• 在参数更新失控和数值异常的共同作用下，训练过程会表现出明显的不稳定性：

  • 损失函数在相邻迭代之间剧烈波动，难以呈现稳定下降趋势；
  • 参数频繁被推离合理区域，使得模型难以逐步逼近最优解；
  • 网络无法稳定地学习有效特征，最终表现为模型性能明显下降。

• 在更极端的情况下，梯度爆炸会使损失函数持续上升，训练过程完全发散，模型无法收敛。

​ 梯度爆炸会先导致数值计算失真，继而引发参数更新失控，最终破坏整个训练过程的稳定性。这种影响会随着网络深度的增加而被进一步放大。

二、梯度爆炸出现的典型场景

本节结合模型结构与训练设置，说明在什么情况下梯度爆炸最容易发生。

​ 梯度爆炸并非偶然现象，而是深度模型结构、训练方式与参数设置共同作用的结果。以下是实践中最常见的三类高发场景。

1. 深层前馈网络（Deep Feedforward Networks）

​ 在深层前馈网络中，梯度在反向传播过程中需要逐层传递，其数学形式可以写为多层雅可比矩阵的乘积。

• 当网络层数$d$很大时，这种连乘结构会带来一个关键问题：

  • 若每一层的梯度范数略大于 1
  • 多层相乘后，整体梯度会呈 指数级放大

• 特别是在以下情况下，梯度爆炸更容易发生：

  • 权重矩阵的谱范数（最大奇异值）大于 1
  • 使用未约束的全连接层
  • 激活函数在某些区间导数较大（如 ReLU 在正区间）

​ 因此，在深层网络中，即使单层看似“正常”的梯度，也可能在整体反向传播过程中被不断放大，最终导致梯度爆炸。

2. 循环神经网络（RNN）与长序列任务

​ 梯度爆炸在 RNN 中尤为典型，其根本原因在于时间维度上的梯度累乘。

​ 在 RNN 中，隐藏状态的更新形式为：

$${\mathbf{h}}^{(t)}=f(\mathbf{W}{\mathbf{h}}^{(t-1)}+\mathbf{U}{\mathbf{x}}^{(t)})$$

​ 在反向传播时，某一时间步的梯度需要经过多个时间步反传。

• 这意味着：
  • 序列越长，梯度连乘项越多
  • 若循环权重矩阵$\mathbf{W}$ 的范数大于 1
  • 梯度会在时间维度上迅速放大
• 因此，在以下任务中梯度爆炸尤为常见：
  • 长文本建模
  • 时间序列预测
  • 语音、金融等长时间依赖任务

​ 这也是 LSTM、GRU 等门控结构被提出的重要动机之一，它们通过门控机制对梯度流进行约束，缓解梯度爆炸与消失问题。

3. 不合理的权重初始化或高学习率

​ 除了模型结构本身，训练超参数设置不当同样会显著放大梯度。

(1) 权重初始化不合理

• 若权重初始值过大，会导致前向传播中激活值迅速增大

• 激活值变大 → 反向传播中梯度也随之放大

• 多层叠加后，梯度可能迅速失控

  例如，当权重矩阵的元素方差过大时，其对应的梯度范数往往也偏大，从而加剧梯度爆炸风险。

(2) 学习率过高

​ 当学习率$\alpha$过大时，即使梯度本身尚可接受，也会导致：

• 参数在一次更新中“跨步过大”
• 模型跳过最优区域
• 损失函数剧烈震荡甚至直接发散

三、梯度爆炸与梯度消失的对比

本节从机制和训练现象角度，对比梯度爆炸与梯度消失的异同。

特性	梯度爆炸	梯度消失
梯度变化	指数增长	指数减小
网络层数影响	层数越多问题越严重	层数越多问题越严重
典型后果	参数更新过大，训练发散	参数几乎不更新，训练停滞
解决策略	梯度裁剪、权重初始化优化、学习率调节	激活函数选择（ReLU）、权重初始化优化、归一化

四、总结

• 梯度爆炸：反向传播中梯度值过大，导致训练不稳定或发散。
• 主要原因：深层网络/长序列 RNN、激活函数特性、权重初始化不当、学习率过高。
• 训练影响：数值溢出、参数更新失控、损失剧烈波动。
• 应对策略：梯度裁剪、优化权重初始化、调节学习率、自适应优化器、改进网络结构（如 LSTM/GRU）

​ 总之，梯度爆炸是深度网络训练中的常见问题，通过梯度裁剪等方法可以有效控制梯度幅度，保证训练稳定性。在实际应用中，结合学习率调整、权重初始化等策略，还能进一步提高深层网络的训练鲁棒性。