三角函数各个公式推理及证明
1. 余弦定理
余弦定理是勾股定理的一般形式,勾股定理是余弦定理的特殊情况,因此,余弦定理是怎么得出来的呢?本文将在勾股定理的基础上推到出余弦定理

如上图所示:三角形ABC,其中AD垂直于BC,则根据勾股定理:
c
2
=
A
D
2
+
D
C
C
c^2 = AD^2+DC^C
c2=AD2+DCC
其中,
A
D
=
b
s
i
n
α
,
D
C
=
a
−
B
D
=
a
−
b
c
o
s
α
AD = bsin\alpha, DC=a-BD=a-bcos\alpha
AD=bsinα,DC=a−BD=a−bcosα将这两个等式带入上式
c
2
=
A
D
2
+
D
C
C
=
(
b
s
i
n
α
)
2
+
(
a
−
b
c
o
s
α
)
2
c^2 = AD^2+DC^C=(bsin\alpha)^2+(a-bcos\alpha)^2
c2=AD2+DCC=(bsinα)2+(a−bcosα)2
c
2
=
b
2
s
i
n
2
α
+
a
2
+
b
2
c
o
s
2
α
−
2
a
b
c
o
s
α
c^2 =b^2sin^2\alpha+a^2+b^2cos^2\alpha-2abcos\alpha
c2=b2sin2α+a2+b2cos2α−2abcosα
c
2
=
b
2
(
s
i
n
2
+
c
o
s
2
α
)
+
a
2
α
−
2
a
b
c
o
s
α
=
b
2
+
a
2
−
2
a
b
c
o
s
α
c^2 =b^2(sin^2+cos^2\alpha)+a^2\alpha-2abcos\alpha = b^2+a^2-2abcos\alpha
c2=b2(sin2+cos2α)+a2α−2abcosα=b2+a2−2abcosα
证明完毕。
2. c o s ( α − β ) = s i n α s i n β + c o s α c o s β cos(\alpha - \beta)=sin\alpha sin\beta+cos\alpha cos\beta cos(α−β)=sinαsinβ+cosαcosβ
证明:
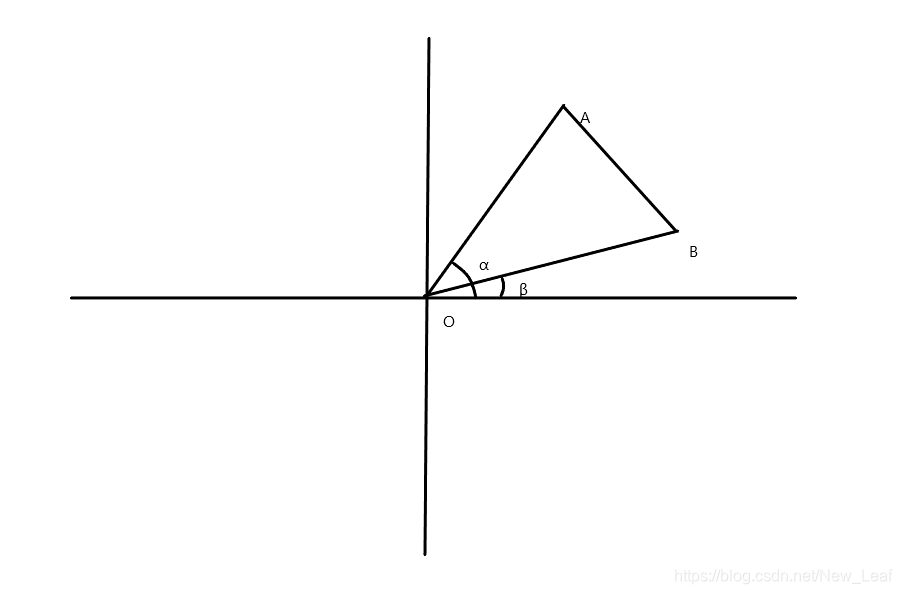
如上图所示,三角形OAB,其中A点坐标客表示为
(
r
a
c
o
s
α
,
r
a
s
i
n
α
)
(r_acos\alpha, r_asin\alpha)
(racosα,rasinα),B点坐标客表示为
(
r
b
c
o
s
β
,
r
b
s
i
n
β
)
(r_bcos\beta, r_bsin\beta)
(rbcosβ,rbsinβ)。则
B
A
⃗
\vec{BA}
BA可以表示为
(
r
a
c
o
s
α
−
r
b
c
o
s
β
,
r
a
s
i
n
α
−
r
b
s
i
n
β
)
(r_acos\alpha-r_bcos\beta, r_asin\alpha-r_bsin\beta)
(racosα−rbcosβ,rasinα−rbsinβ),则其长度的平方为:
∣
B
A
⃗
∣
2
=
(
r
a
c
o
s
α
−
r
b
c
o
s
β
)
2
+
(
r
a
s
i
n
α
−
r
b
s
i
n
β
)
2
|\vec{BA}|^2 = (r_acos\alpha-r_bcos\beta)^2+(r_asin\alpha-r_bsin\beta)^2
∣BA∣2=(racosα−rbcosβ)2+(rasinα−rbsinβ)2
展开化简得:
∣
B
A
⃗
∣
2
=
r
a
2
+
r
b
2
−
2
r
a
r
b
(
c
o
s
α
c
o
s
β
+
s
i
n
α
s
i
n
β
)
|\vec{BA}|^2 = r_a^2+r_b^2-2r_ar_b(cos\alpha cos\beta+sin\alpha sin\beta)
∣BA∣2=ra2+rb2−2rarb(cosαcosβ+sinαsinβ)
同理,根据三角形的余弦定理,
∣
A
B
∣
2
=
∣
O
A
∣
2
+
∣
O
B
∣
2
−
2
∣
O
A
∣
∣
O
B
∣
c
o
s
(
α
−
β
)
|AB|^2 = |OA|^2+|OB|^2-2|OA||OB|cos(\alpha-\beta)
∣AB∣2=∣OA∣2+∣OB∣2−2∣OA∣∣OB∣cos(α−β),而|OA|的长度为
r
a
r_a
ra,|OB|的长度为
r
b
r_b
rb,代入方程得,
∣
B
A
⃗
∣
2
=
r
a
2
+
r
b
2
−
2
r
a
r
b
c
o
s
(
α
−
β
)
|\vec{BA}|^2 = r_a^2+r_b^2-2r_ar_bcos(\alpha-\beta)
∣BA∣2=ra2+rb2−2rarbcos(α−β)
比较上两式得,
c
o
s
(
α
−
β
)
=
s
i
n
α
s
i
n
β
+
c
o
s
α
c
o
s
β
cos(\alpha - \beta)=sin\alpha sin\beta+cos\alpha cos\beta
cos(α−β)=sinαsinβ+cosαcosβ
证毕





 本文详细介绍了余弦定理的推导过程,从勾股定理出发,通过几何图形解析得出余弦定理的证明。此外,还证明了三角恒等式cos(α−β)=sinαsinβ+cosαcosβ,通过坐标系中三角形的边长计算,利用余弦定理得出结论。
本文详细介绍了余弦定理的推导过程,从勾股定理出发,通过几何图形解析得出余弦定理的证明。此外,还证明了三角恒等式cos(α−β)=sinαsinβ+cosαcosβ,通过坐标系中三角形的边长计算,利用余弦定理得出结论。
















 3045
3045

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








