计算轴向磁铁和环状磁铁的磁场（Matlab代码实现）

 💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

 ⛳️赠与读者

👨‍💻做科研，涉及到一个深在的思想系统，需要科研者逻辑缜密，踏实认真，但是不能只是努力，很多时候借力比努力更重要，然后还要有仰望星空的创新点和启发点。当哲学课上老师问你什么是科学，什么是电的时候，不要觉得这些问题搞笑。哲学是科学之母，哲学就是追究终极问题，寻找那些不言自明只有小孩子会问的但是你却回答不出来的问题。建议读者按目录次序逐一浏览，免得骤然跌入幽暗的迷宫找不到来时的路，它不足为你揭示全部问题的答案，但若能让人胸中升起一朵朵疑云，也未尝不会酿成晚霞斑斓的别一番景致，万一它居然给你带来了一场精神世界的苦雨，那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。

     或许，雨过云收，神驰的天地更清朗.......🔎🔎🔎

💥1 概述

计算具有任意和均匀磁化（例如轴向和直径向磁化圆柱体作为特例）的圆柱形和环形永磁体的磁场和磁场梯度，或者等效地计算轴向螺线管。这些函数可用于计算永磁体圆柱体施加给磁偶极子的扭矩和力（分别为磁场和磁场梯度）。
计算具有轴向或直径向磁化的同轴永磁体圆柱体之间的力和力矩。
可视化磁场和磁场梯度的函数。注：此库中实现的表达式基于均匀磁化的基本假设，这对于由现代高级磁性材料（如SmCo、NdFeB或磁化率
  <0.1
  负磁铁等）制成的磁铁是一个优秀的近似。与常见的数值方法（如有限元（FE）方法或直接数值积分）相比，其主要优点是快速的计算时间，约为微秒级，这使得高效的多变量参数空间分析和解决永久磁铁排列的全局优化问题成为可能。

一、轴向磁铁与环状磁铁的定义及结构参数

1. 轴向磁铁

• 定义：磁化方向平行于几何轴线，南北极分布于端面。

   

  

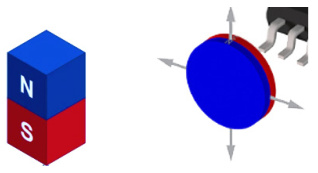
  • 典型结构：圆柱/圆盘/环形，磁力线沿轴线闭合。
  • 磁化方向：轴向磁化（沿厚度方向）为主，少数为径向磁化。

• 关键参数：

   

  

   

  

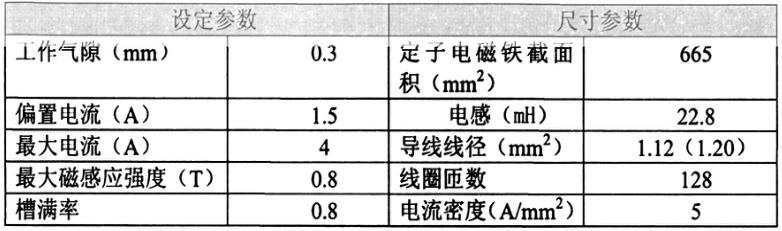
  参数类型	示例值	物理意义
  工作气隙	0.3 mm	磁场有效作用距离
  最大磁感应强度	0.8 T	磁场强度上限
  定子截面积	665 mm²	磁路截面积影响磁场强度
  线圈匝数	128	电流与磁场的转换效率

2. 环状磁铁

• 定义：中心有孔的环形磁体，磁场集中于环内，外部磁场弱。

  • 磁化方向：分轴向（N/S极在上下表面）或径向（N/S极在内/外壁）。
  • 特点：高磁场稳定性、抗干扰性强。

• 关键参数：

  

  型号示例	外径/内径/高度	磁化强度	磁力	应用场景
  R-06-02-02	6 mm/2 mm/2 mm	N45	0.38g	微型传感器（小空间）
  R-10-05-05	10 mm/5 mm/5 mm	N50	2.5 kg	工业电机（高负载）

---

二、磁场分布模型及影响因素

1. 轴向磁铁磁场分布

• 模型特征：
  • 磁场沿轴线对称，中心强度最高。

    

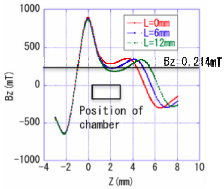
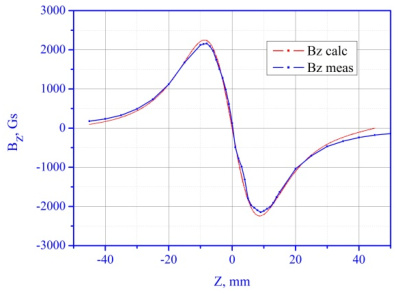
  • 磁铁间距（L）增大时，磁场强度波动范围扩大（图5，）。
• 影响因素：
  • 磁化方向：轴向磁化比径向磁场更均匀。

    

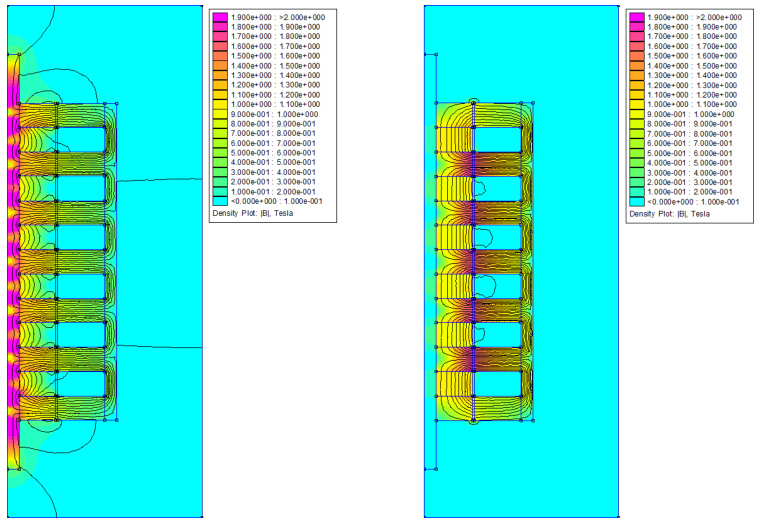
  • 材料等级：N52钕磁铁比N35磁场强度高30%。
  • 温度：>80°C时钕磁铁磁场衰减。

2. 环状磁铁磁场分布

• 模型特征：
  • 轴向磁化：磁场线从N极垂直穿出，在环中心形成平行场。
  • 径向磁化：磁场集中于内壁/外壁，中心区域弱。
• 解析模型：
  • 标量磁位法结合二项式定理，误差<7%。
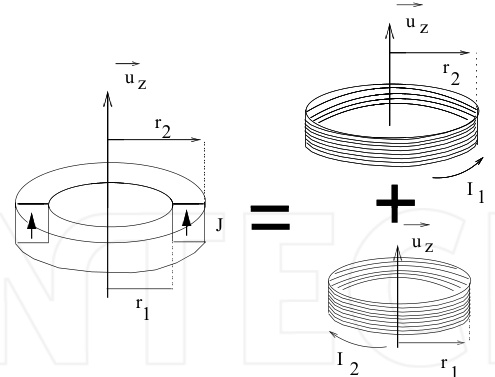
  • 安培等效模型：分解为同心圆环电流（图2，）。

    

---

三、磁场计算方法对比

方法	适用磁铁类型	公式/原理	精度特点
安培环路定理	环状磁铁	B=μ0NI2πrB=2πrμ0​NI​	轴对称场适用，计算高效
磁荷模型	轴向/环状	表面电荷密度积分	需数值积分，精度高
有限元仿真（CST/COMSOL）	复杂结构	三维网格划分求解麦克斯韦方程	精度>95%，耗时长
切片求和法	轴向磁铁	分割矩形截面螺线管叠加磁场	实验验证误差<5%

注：环状磁铁径向极化时，库仑模型与安培模型结果一致。

---

四、实际应用案例

1. 轴向磁铁应用

• 磁悬浮轴承：
  • 参数：偏置电流1.5A，槽满率0.8，实现零摩擦悬浮。
• 离子源装置：
  • 优化磁铁间距（L=6mm）提升轴向磁场均匀性。

2. 环状磁铁应用

• 永磁轴承：

  

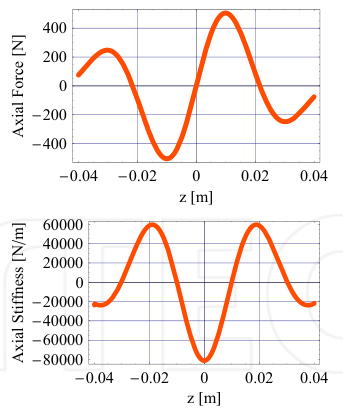
  • 5环堆叠时轴向刚度周期性波动，适用于精密旋转设备。
• 多极磁铁系统：
  • 四极/七极钕磁铁构建梯度磁场，偏转原子轨迹精度达99%。

3. 磁场优化技术

• 削斜工艺：修正二极磁铁场梯度指数。
• 镜像板加载：减少磁场畸变（同文献）。

---

五、研究挑战与前沿

1. 高温超导磁铁：突破钕磁铁80°C工作限制。
2. 动态磁场测量：矩阵线圈技术捕捉快脉冲磁铁瞬态响应。
3. 生物安全性：强磁场干扰心脏起搏器（案例，）。

设计建议：

• 轴向磁铁优选N50+等级，环状磁铁需明确磁化方向（轴向/径向）。
• 高精度场景建议结合Ansoft Maxwell仿真与实验标定。

  

  查看

📚2 运行结果

部分代码：

%% DEMO 1 - test functions to visualize a cylindrical magnet
% this demo shows how to run the visualization function 
% drawCylindricalMagnet
% To use this function, the user simply needs to know the following
% parameters: 
%   - position (magnet origin or center)
%   - orientation (i.e., the axis of the cylinder as a unit vector)
%   - radius (in meters)
%   - length (in meters)

currentPath = pwd;                          % store current path
cd ..                                       % move to parent directory
addpath(genpath("Functions and Scripts"))   % add folder to path

position = [0 0 0];                         % magnet origin m.u. [m]

% generate random orientation
orientation = 2*rand(1,3) - [1 1 1];
orientation = orientation/norm(orientation);

% note: since this is the code for an axial cylindrical magnet, the body is
% symmetric w.r.t. its axis (i.e., the cylinder axis). Thus its orientation
% can be simply described by the normalized magnetization vector.

figure
x0     = 10;
y0     = 110;
width  = 1260;
height = 480;
set(gcf,'position',[x0,y0,width,height])
subplot(251)
drawCylindricalMagnet(0.004,0.004,[position 0 0 1],'texture','axial')
axis([-0.01 0.01 -0.01 0.01 -0.01 0.01])
title('AXIAL, $\mathbf{m} = [\,0\quad 0\quad 1\,]$','interpreter','latex')
subplot(252)
drawCylindricalMagnet(0.004,0.004,[position 0 0 -1],'texture','axial')
axis([-0.01 0.01 -0.01 0.01 -0.01 0.01])
title('AXIAL, $\mathbf{m} = [\,0\quad 0\; -1\,]$','interpreter','latex')
subplot(253)
drawCylindricalMagnet(0.004,0.004,[position 1 0 0],'texture','axial')
axis([-0.01 0.01 -0.01 0.01 -0.01 0.01])
title('AXIAL, $\mathbf{m} = [\,1\quad 0\quad 0\,]$','interpreter','latex')
subplot(254)
drawCylindricalMagnet(0.004,0.004,[position 0 1 0],'texture','axial')
axis([-0.01 0.01 -0.01 0.01 -0.01 0.01])
title('AXIAL, $\mathbf{m} = [\,0\quad 1\quad 0\,]$','interpreter','latex')
subplot(255)
drawCylindricalMagnet(0.004,0.004,[position 0 0 1],'texture','diametric')
axis([-0.01 0.01 -0.01 0.01 -0.01 0.01])
title('DIAMETRIC, $\mathbf{m} = [\,0\quad 0\quad 1\,]$','interpreter','latex')
subplot(256)
drawCylindricalMagnet(0.004,0.004,[position 1 0 0],'texture','diametric')
axis([-0.01 0.01 -0.01 0.01 -0.01 0.01])
title('DIAMETRIC, $\mathbf{m} = [\,1\quad 0\quad 0\,]$','interpreter','latex')
subplot(257)
drawCylindricalMagnet(0.004,0.004,[position 1/sqrt(2) 1/sqrt(2) 0])
title('NORMAL, $\mathbf{m} = [\,1/\sqrt{2}\quad 1/\sqrt{2}\quad 0\,]$','interpreter','latex')
axis([-0.01 0.01 -0.01 0.01 -0.01 0.01])

🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。

[1]王瑞凯,左洪福,吕萌.环形磁铁空间磁场的解析计算与仿真[J].航空计算技术, 2011, 41(5):5.DOI:10.3969/j.issn.1671-654X.2011.05.005.

[2]赵国生,彭全岭,杨向臣.磁通法在强磁场混合型永久磁铁中应用研究[J].中国稀土学报, 2015, 33(5):6.DOI:10.11785/S1000-4343.20150501.

[3]杨达起.对影响定向磁铁磁场分布因素的分析[J].磁记录材料, 1985(04):20-23.DOI:CNKI:SUN:CXJL.0.1985-04-005.

🌈4 Matlab代码实现

资料获取，更多粉丝福利，MATLAB|Simulink|Python资源获取

                                                           ​