斜率优化 笔记

说道斜率优化，我就想起今年下半年 湖南2008年的一个题。相信大家也不陌生（如果您是第一次学斜率优化，那估计挺陌生的）。题目叫：HNOI2008 玩具装箱TOY。题意大概是这个样子：

题意简述

给你一个序列$a_{[1,n]}$和一个常数$k$。请你把这个序列分成若干段。定义：一个段$[l,r]$需要占用的空间$X$就等于$r-l+\sum _{i=l}^r{a}_i$，然后需要的花费就是$(X-k{)}^2$。其中这个$X$没有限制，珂以无限长（只不过不是最优就是了）。请求出所有段的花费的最小值。

暴力思路

如果您来看斜率优化的话，相信您也不难退出这个题的暴力$dp$。设$dp[i]$表示前$i$个数分成一些段使得总花费最小。那么，$dp[i]=mindp[j]+cost(j+1,i)$。其中$cost(j+1,i)$表示从$j+1$到$i$这些数在一段的花费。为了稍微快一点，设$sum$表示$a$的前缀和。那么$cost(j+1,i)$就等于$[(i-j-1+sum[i]-sum[j])-l{]}^2$。

但是这个$dp$是$O(n^2)$的。能不能再快一点呢？（严格来讲，你必须要再快一点，要不然这个时间就卡不过去）

正片开始：斜率优化

把关于$i$的项和关于$j$的项单独提出来。变成：

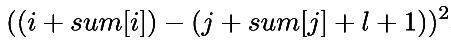
设$a(x)=x+sum[x],b(x)=x+sum[x]+l+1$。那么原式等于$(a(i)-b(j){)}^2$。

稍稍改变$j$的定义，令$j$是满足条件中最优的$j$。

那么：（推式子警告）

$$\begin{gathered} dp[i]=dp[j]+(a(i)-b(j){)}^2 \\ dp[i]=dp[j]+a(i{)}^2-2a(i)b(j)+b(j{)}^2 \\ dp[i]+2a(i)b(j)-a(i{)}^2=dp[j]+b(j{)}^2 \end{gathered}$$

把这个式子放到平面直角坐标系上，以$b(j)$为$x$，$dp[j]+b(j{)}^2$为$y$。

对于每个$j$来说，点$(b(j),dp[j]+b(j{)}^2)$就是一个决策点了。

而且，显然这是一个直线的关系，它的斜率就是$2a(i)$，截距是$dp[i]-a(i{)}^2$。我们把直线向上平移$a(i{)}^2$，就是最小的$dp[i]$。由于$a(i{)}^2$的值是确定的（我们在找$j$的过程中，$i$是不会变的），所以在同一个$i$里面，我们相当于要让截距最小。

这样，对于每个$i$（注意，和上面不一样，不在同一个$i$里面了），珂能作为最优点选择出来的点应该组成一个下凸包（因为$a(i)$是单调递增的，所以斜率单调递增，即组成下凸包）。

（$a(i)$的单调递增性我就不讲了）

为啥？考虑这种情况：

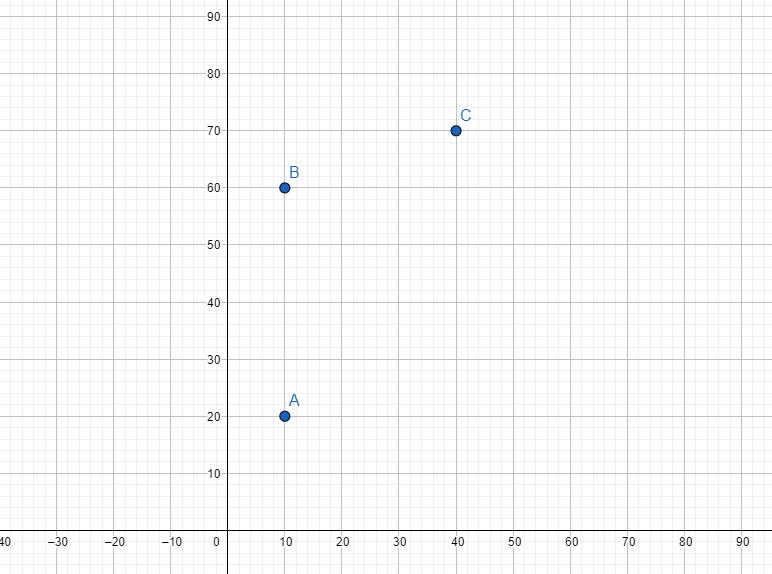
（$A$，$B$，$C$是珂供选择的三个决策点）

当前的话，如果$A$还没滚蛋，应该是$A$比$B$优的。如图

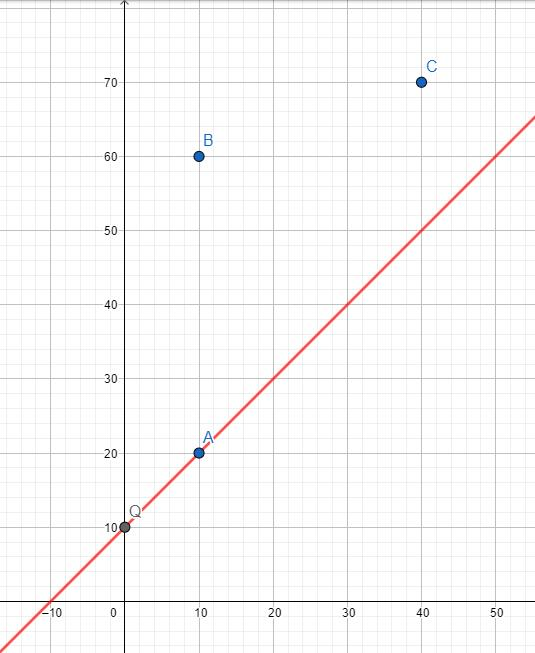
随着斜率的增加，也许会出现$C$比$A$和$B$都优的情况。如图：

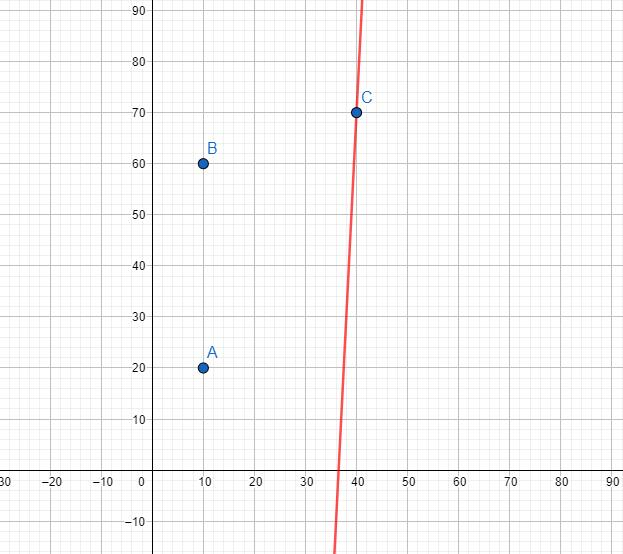
容易证明，$C$此时一枝独秀，$A$和$B$都珂以滚蛋了。这两种情况有一个共同点，就是$B$都不能再优了。anyway，滚蛋吧。

还有一种情况（肯定还有，只有刚刚那一个是没法保证正确性的），就是最前面两个元素还要满足一个条件：第一个点和第二个点之间的斜率要$>=2a(i)$，否则第一个就再也不珂能作为最优解出现了，因为此时随着斜率的单调递增，后面的斜率肯定会更大，在当下的$2a(i)$的斜率中第二个都比第一个优，后面的话就不知道优到哪里去了。所以第一个就再起不能，滚了。

如图：

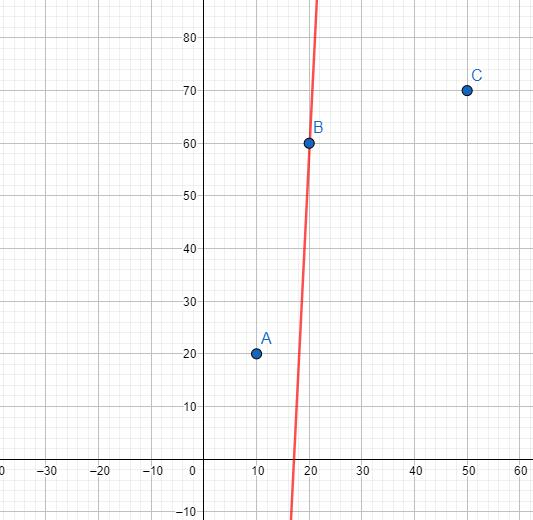
还是刚刚那张图，不过是另一种滚蛋方法。此时红色直线的斜率=$2a(i)$=$20$。当红色直线斜率为$20$的时候，$A$就没有$B$优了。如果再高一点，显然，还是没有$B$优。所以以后这个$A$都不珂能比$B$更优了。$A$就珂以滚蛋了。

说道这里，我们发现，这个东西珂以用一个单调队列维护。维护完一个正确的队列之后，$Q[head]$就是最优解。

设队列为$Q$，首尾分别叫$head,tail$。

总结一下，就是要维护两个关系：

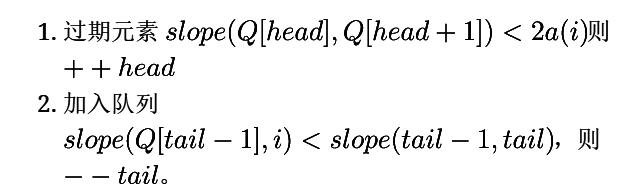
代码：

#include<bits/stdc++.h>
using namespace std;
namespace Flandre_Scarlet
{
	#define N 112345
	#define int long long 

	#define F(i,l,r) for(int i=l;i<=r;++i)
	#define D(i,r,l) for(int i=r;i>=l;--i)
	#define Fs(i,l,r,c) for(int i=l;i<=r;c)
	#define Ds(i,r,l,c) for(int i=r;i>=l;c)
	#define Tra(i,u) for(int i=G.Start(u);~i;i=G.Next(i))
	#define MEM(x,a) memset(x,a,sizeof(x))
	#define FK(x) MEM(x,0)
	int n,l;
	int c[N];
	void R1(int &x)
	{
	    x=0;char c=getchar();int f=1;
	    while(c<'0' or c>'9') f=(c=='-')?-1:1,c=getchar();
	    while(c>='0' and c<='9') x=(x<<1)+(x<<3)+(c^48),c=getchar();
	    x=(f==1)?x:-x;
	}
	void Input()
	{
		R1(n),R1(l);
		F(i,1,n) R1(c[i]),c[i]+=c[i-1];
	}

	int Q[N];
	int dp[N];
	int a(int i){return c[i]+i;}
	int b(int i){return c[i]+i+l+1;}
	int x(int i){return b(i);}
	int y(int i){return dp[i]+b(i)*b(i);}
	int slope(int i,int j)//计算斜率
	{
		return (y(i)-y(j))/(x(i)-x(j));
	}
	void Soviet()
	{
		int head=1,tail=1;
		F(i,1,n)
		{
			while(head<tail and slope(Q[head],Q[head+1])<2*a(i)) ++head;
                        //垃圾决策点出队列
			dp[i]=dp[Q[head]]+(a(i)-b(Q[head]))* (a(i)-b(Q[head]));
			//Q[head]就是最优的决策点。
			while(head<tail and slope(i,Q[tail-1])<slope(Q[tail-1],Q[tail])) --tail;
			Q[++tail]=i;
                        //把i加入队列
		}
		printf("%lld\n",dp[n]);
	}
	void IsMyWife()
	{
		Input();
		Soviet();
	}
	#undef int //long long 
}
int main()
{
	Flandre_Scarlet::IsMyWife();
	getchar();getchar();
	return 0;
}

还有一些答疑时间（根据作者自身出现的理解问题编写，以后支持评论功能之后珂能会根据评论区中的问题编写。）

Q：既然$Q[head]$是最优的，为啥还要存着后面的点呢？
A：后面的点虽然现在不是最优的，但是它们很有潜力，等以后斜率上去之后，也许$Q[head]$就滚蛋了，后面那些点就变成了最优。注意上面，我们说的是珂能成为最优的点，而不是现在最优的点。要为未来着想。