数据结构：AVL树与伸展树

1.AVL Tree

核心思想：AVL Tree中每个节点都会有一个值，为depth(left)-depth(right)，理想状态下为了维持平衡，这个值应当为-1，0，1。倘若这个值在insert or remove后变为-2或者2，则需要通过旋转进行变换。

旋转：（1）单旋转：LL与RR

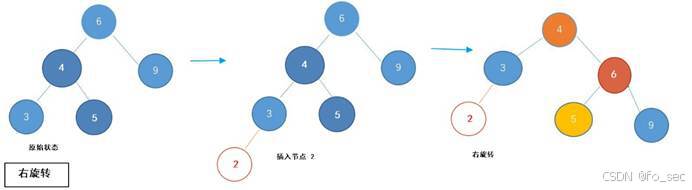
如图，当插入2后，6的值为2（左深3右深1），所以要对6进行LL旋转。具体如下：

def LL:

       let node* temp equal root->left (temp will be the root in future)

       root->left equal to temp->right

       temp->right equal to root

       temp->height equal to (max of height(t->left) and height(t->right)) plus 1

       root->height equal to (max of height(temp->left),height(root)) plus 1

具体代码如下：

template<class KEY,class OTHER>

void AVLTree<KEY, OTHER>::LL(AVLNode*& t)

{

       AVLNode* t1 = t->left; //未来的树根

       t->left = t1->right;

       t1->right = t;

       t->height = max(height(t->left), height(t->right)) + 1;

       //此处的+1是t自己为树提供的高度！！

       t1->height = max(height(t1->left), height(t)) + 1;

}

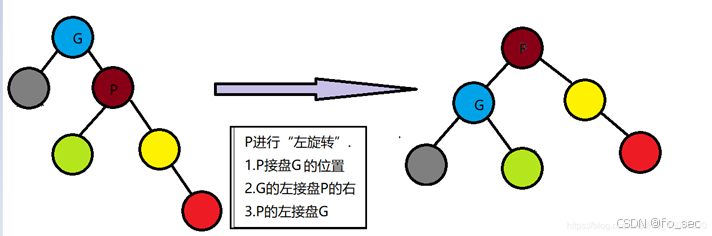
同理，可以得到对称的右旋RR，具体代码如下

template<class KEY,class OTHER>

void AVLTree<KEY, OTHER>::RR(AVLNode*& t)

{

       AVLNode* t1 = t->right;

       t->right = t1->left;

       t1->left = t;

       t->height = max(height(t->left), height(t->right)) + 1;

       t1->height = max(height(t1->right), height(t)) + 1;

       t = t1;

}

（2）多旋转：LR与RL

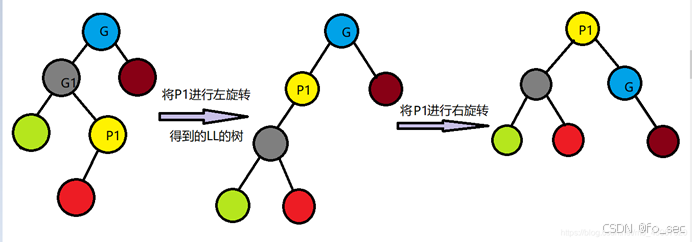
此时对G来说，导致它更深的是LR（左枝的右枝），所以要进行LR旋转。

实际上LR旋转可以先通过RR(root->left)转化为LL形式，而后通过LL(root)旋转即可。

伪代码如下：

def LR:

       RR(root->left)

       LL(root)

代码如下：

template<class KEY,class OTHER>

void AVLTree<KEY, OTHER>::LR(AVLNode*& t)

{

       RR(t->left);

       LL(t);

}

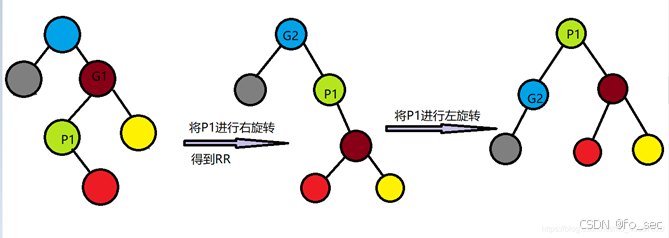
对称的，我们可以得到RL的旋转方法。

template<class KEY,class OTHER>

void AVLTree<KEY, OTHER>::RL(AVLNode*& t)

{

       LL(t->left);

       RR(t);

}

2.伸展树

伸展树用于保证连续M次对树操作最多花费O(MlogN)，但是不保证每次访问花费θ(logN)，也就是说伸展树可以保证整体的平均访问速度，但是不确保个体的访问速度。

其基于这样的基本事实：二叉查找树的每次操作最坏情况O(N)并不坏，只需要很少发生即可。

当我们深入访问了一个节点后，我们必须对其进行移动！因为经验表明，访问一次后很大概率会多次访问！

其基本思路是：当一个节点被访问后，通过AVL树旋转向根推进。

实施方法：展开：

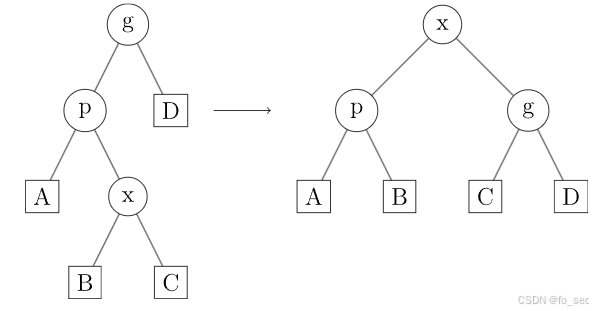
（1）面对LR（RL）则使用LR（RL）旋转即可

（2）面对LL（RR）进行对称镜像操作

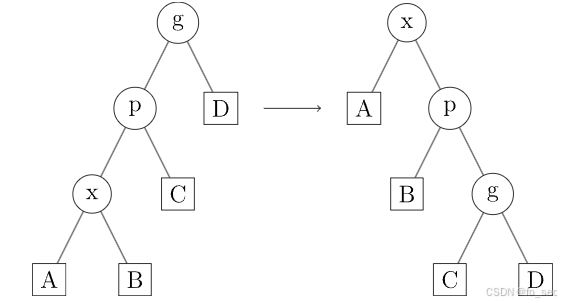
看起来没什么区别，但是展开操作不仅能将访问节点移动到根处，还能降路径上大部分节点深度大致减少一半的效果。