AVL树和伸展树-二叉树-数据结构与算法

最新推荐文章于 2025-03-01 22:41:35 发布

原创最新推荐文章于 2025-03-01 22:41:35 发布 · 417 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#二叉树

数据结构与算法专栏收录该内容

15 篇文章

订阅专栏

本文深入探讨了AVL树和伸展树这两种高效的数据结构。AVL树作为高度平衡的二叉查找树，确保了在各种操作下树的高度保持在log2n级别，避免了退化为链状结构的情况。伸展树则是一种特殊的二叉查找树，通过旋转机制将最近访问的节点提升为树根，加速了后续对该节点的访问。两种树结构都致力于提高搜索效率，适用于需要频繁查找操作的场景。

AVL树(高度平衡树)
AVL树是高度平衡的二叉树。它的特点是：树中任何节点的两个子树的高度最大差别为1

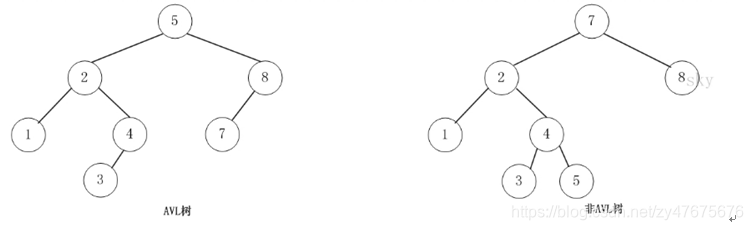
结构体定义:

class AVLTreeNode{
    public:
        T key;                // 关键字(键值)
        int height;         // 高度
        AVLTreeNode *left;    // 左孩子
        AVLTreeNode *right;    // 右孩子
        AVLTreeNode(T value, AVLTreeNode *l, AVLTreeNode *r):
            key(value), height(0),left(l),right(r) {}
};

增加和删除可能要通过一次或多次树旋转来重新平衡这个树。
特点：
1．本身是一颗二叉查找树
2. 带有平衡条件：每个结点的左右子树的高度之差的绝对值（平衡因子）最多为1。
AVL树，本质上是带了平衡功能的二叉查找树

AVL树的作用：
对于一般的二叉查找树，其期望高度（即一颗平衡树时）为log2n，其各操作的时间复杂度（O(log2n)）同时也由此决定。但是，在某些极端的情况下（如插入的序列是有序时），二叉查找树将会退化成近似链或链。此时，其操作的时间复杂度将退化成线性的，即O(n)。
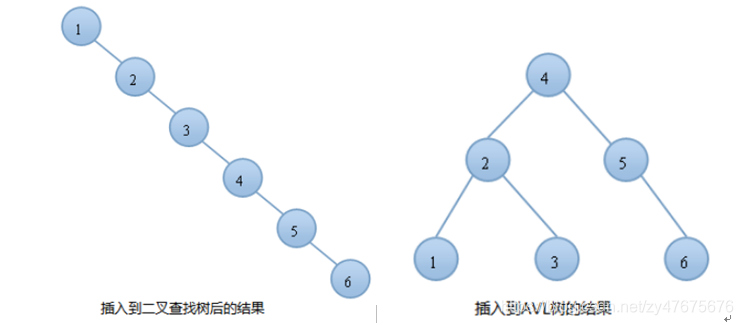
在这里插入图片描述
由上图可知，同样的结点，由于插入的方式不同导致树的高度也有所不同。特别是在带插入节点个数很多且正序的情况下，会导致二叉树的高度是N,而二叉查找树的高度始终为log2n。高度越小，对树的一些基本操作的时间复杂度就会越小。

2.伸展树(Splay Tree)
伸展树是一种特殊的二叉查找树，它还具备一个特点：当某个结点被访问时，伸展树会通过旋转使该节点成为树根。这样的好处是，下次要访问该节点时，能够迅速的访问该节点。

class SplayTreeNode{
    public:
        T key;                // 关键字(键值)
        SplayTreeNode *left;    // 左孩子
        SplayTreeNode *right;    // 右孩子
        SplayTreeNode():left(NULL),right(NULL) {}
        SplayTreeNode(T value, SplayTreeNode *l, SplayTreeNode *r):
            key(value), left(l),right(r) {}
};