6.斐波那契堆
斐波那契堆相比于普通的二项堆,在摊还分析时具有更好的时间复杂度:
|
操作 |
二项堆 (最坏情况) |
斐波那契堆 (摊还) |
|
MAKE-HEAP |
Θ(1) |
Θ(1) |
|
INSERT |
Θ(lgn) |
Θ(1) |
|
MINIMUM |
Θ(1) |
Θ(1) |
|
EXTRACT-MIN |
Θ(lgn) |
Θ(lgn) |
|
UNION |
Θ(n) |
Θ(1) |
|
DECREASE-KEY |
Θ(lgn) |
Θ(1) |
|
DELETE |
Θ(lgn) |
Θ(lgn) |
然而从实际角度看,除了管理大量数据的应用外,斐波那契堆的常数因子和编程复杂度使得其比起普通k项堆并不使用。所以其研究主要出于理论兴趣。如何开发出和斐波那契堆一样时间复杂度但是简单的数据结构仍待创新。
1.斐波那契堆的结构:
斐波那契堆是一系列具有最小堆序的有根树集合。也就是说,在里面每棵树都是一个最小堆。如下图。
其每个节点x包含一个指向其父节点的指针x.p和指向孩子的指针x.child。x所有节点都被连接成一个环形双向链表,称为x的孩子链表。孩子链表中每个孩子都有指针y.left与y.right。
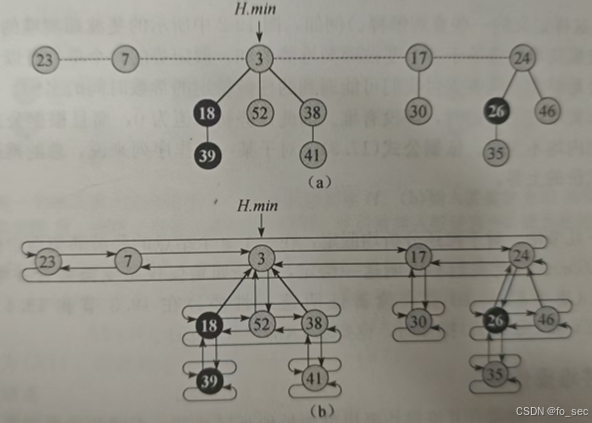
加入双向链表有两个有点:第一,可以在O(1)时间内从一个环形双向链表的任何位置插入一个节点或者删除一个节点。第二,给定两个这种链表,可以在O(1)内将它们连接形成一个新的环状链表。
同时,每个节点x还会有两个属性。x.degree用于记录x的孩子链表中孩子数目。bool x.mark用于记录x自上一次成为另一个节点的孩子后,是否失去过孩子。
通过指针H.min访问一个给定的斐波那契堆H,此指针指向具有最小关键字的树的根节点。将其称为斐波那契堆的最小节点。
势函数:
对于给定斐波那契堆H,用t(H)表示H中根链表中树的数目,用m(H)来表示H中已标记的结点数目。则斐波那契堆H的势函数Φ(H)如下:
![]()
2.可合并堆操作:
斐波那契堆上的一些可合并堆操作要尽可能长的延后执行。从而使不同操作进行性能平衡。例如,从空斐波那契堆开始,插入k个节点,斐波那契堆将由一个正好包含k个节点的根链表组成。如果在斐波那契堆H上执行EXTRACT-MIN操作,在移除H.min指向的节点后,必须遍历k-1个根节点寻找最小节点,这将带来性能平衡问题。所以需要在执行EXTRACT-MIN操作中遍历根链表,并把节点合并到最小堆树中减小链表规模。不论在执行之前是什么样子,执行后每个节点要求有一个与根链表其他节点均不同的度数,这使得根链表规模最大是Dn+1。
(1)创建新的斐波那契堆
此时H.n=0,H.min=NIL,H中不存在树。则tH=0并且mH=0,故其势ΦH=0,故MAKE-FIB-HEAP摊还代价为实际代价O(1)
(2)插入节点
伪代码:
def FIB-HEAP-INSERT(H,x):
x.degree=0
x.p=NIL
x.child=NUL
x.mark=FALSE
if H.min==NUL
create a root list for H containing just x
H.min=x
else insert x into H’s root list
if x.key<H.min.key
H.min=x
H.n++
显然,其直接将新加入的点丢成新的树将其与其他根连起来即可。
其中,设H为输入的斐波那契堆,H'为结果斐波那契堆,那么:
![]()
势的增量为:
![]()
由于实际代价为O(1),故摊还代价为O1+1=O(1)
(3)寻找最小节点
由于可以直接访问H.min得到,所以实际代价为O(1),势无变化为0,故摊还代价为O(1)
(4)两个斐波那契堆的合并
伪代码:
def FIB-HEAP-UNION(H1,H2):
H=MAKE-FIB-HEAP()
H.min=H1.min
Concatenate the root list of H2 with the root list of H
if (H1.min==NIL) or (H2.min≠NIL and H2.min.key<H1.min.key)
H.n=H1.n+H2.n
return H
也就是确定一个H.min即可,随后将两个链表串起来即可。
其中势函数变化为:
![]()
因为:
![]()
故FIB-HEAP-UNION摊还代价等于实际代价O(1)
(5)抽取最小节点:
这是最为复杂的一个过程。
伪代码如下:其中引入辅助过程CONSOLIDATE,稍后介绍。
def FIB-HEAP-EXTRACT-MIN(H)
z=H.min
if z!=NIL
for each child x of z
add x to the root list of H
x.p=NIL
remove z from the root list of H
if z==z.right
H.min=NIL
else
H.min=z.right
CONSOLIDATE(H)
H.n=H.n-1
return z
其先将最小子节点每个孩子变为根节点,并删除最小节点,然后通过把具有相同度数的根节点合并的方法来链接成根链表,直到每个度数至多只有一个根在链表中。
其中,合并操作就是其中的函数CONSOLIDATE,具体操作过程如下图所示。
合并可以视为重复以下步骤:1.在根链表中找到两个具有相同度数的根x与y。假定x.key<y.key
2.把y链接到x:从根链表移除y,调用FIB-HEAP-LINK过程,使y为x的孩子。将x.degree增加1,并清除y上的标记。
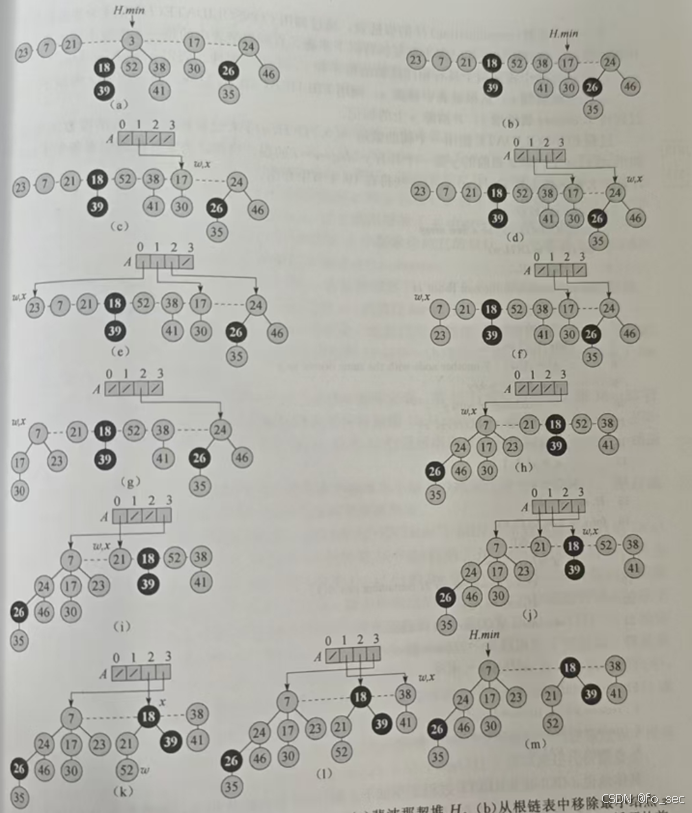
伪代码如下:
def CONSOLIDATE(H)
let A[0..D(H.n)] be a new array
for i=0 to D(H.n)
A[i]=NIL
for each node w in the root list of H
x=w
d=x.degree
while A[d]!=NIL
y=A[d]
if x.key>y.key
exchange x with y
FIB-HEAP-LINK(H,y,x)
A[d]=NIL
d=d+1
A[d]=x
H.min=NIL
for i=0 to D(H.n)
if A[i]!=NIL
if H.min==NIL
create a root list for H containing just A[i]
H.min=A[i]
else insert A[i] into H’s root list
if A[i].key<H.min.key
H.min=A[i]
def FIB-HEAP-LINK(H,y,x)
remove y from the root list of H
make y a child of x, incrementing x.degree
y.mark=FALSE
在其中,array A起到了HASH表的作用,用于记录每个度数下有哪些点。而在while Ad!=NIL起到了合并的作用,使得相同度数的进行合并。
下分析其复杂度:FIB-HEAP-EXTRACT-MIN最多处理最小节点的D(n)个孩子,再加上CONSOLIDATE的其他操作,共计时间代价为O(D(n))。在分析CONSOLIDATE的for循环代价,因为原始根链表中有t(H)个节点,减去抽取出的节点,再加上抽取出的节点的孩子节点(至多为D(n)),故调用CONSOLIDATE时根链表最大为Dn+tH-1。而在for循环中里的while迭代次数取决于根链表,而while是将根链表进行连接,所以我们可以知道其总次数最多为根链表根的数目。因此,for工作量最多与Dn+t(H)成正比。所以抽取最小节点的实际总工作量为O(Dn+t(H))。
而抽取前的势为tH+2m(H),因为最多有Dn+1个根留下且在该过程中没有任何节点被标记,所以此操作后势最大为Dn+1+2m(H)。所以摊还代价最多为:
![]()
![]()
![]()
因此可以增大势的单位来支配隐藏在O(tH)中的常数。直观上讲,由于每次连接操作均把根数目减小1,因此每次链接操作的代价可以由势的减小来支付。
(6)关键字减值和删除节点
关键字减值:假定一个链表中删除一个节点不会改变被移除节点的任何结构属性
伪代码:
def FIB-HEAP-DECREASE-KEY(H,x,k)
if k>x.key
error “new key is greater than current key”
x.key=k
y=x.p
if y!=NIL and x.key<y.key
CUT(H,x,y)
CASCADING-CUT(H,y)
if x.key<H.min.key
H.min=x
def CUT(H,x,y)
remove x from the child list of y, decrementing y.degree
add x to the root list of H
x.p=NIL
x.mark=FALSE
def CASCADING-CUT(H,y)
z=y.p
if z!=NIL
if y.mark=FALSE
y.mark=TRUE
else CUT(H,y,z)
CASCADING-CUT(H,z)
其运行过程如下:
首先保证新的关键字不比x当前的关键字大,然后将新的关键字赋值给x。如果x是根节点,或者x.key≥y.key,那么不需要进行结构上的任何改变,因为没有违反最小堆序。
如果违反了最小堆序。那么:首先切断(CUT)x,切断x与父节点y的连接,从而使x成为一个根节点。
因为x可能是父节点y被链接到另一个节点后被切掉的第二个孩子,所以采取CASCADING-CUT操作。如果y是一个根节点,那么其将会在第二行测试时返回。如果是未被标记的点,因为已经被切掉孩子,那么将会在此时标记。如果是标记过的,此时两个孩子都被切,则y在else里被CUT,然后再对父节点继续进行CASCADING-CUT操作。直到遇到根节点或者未被标记的点。
具体流程如下图。
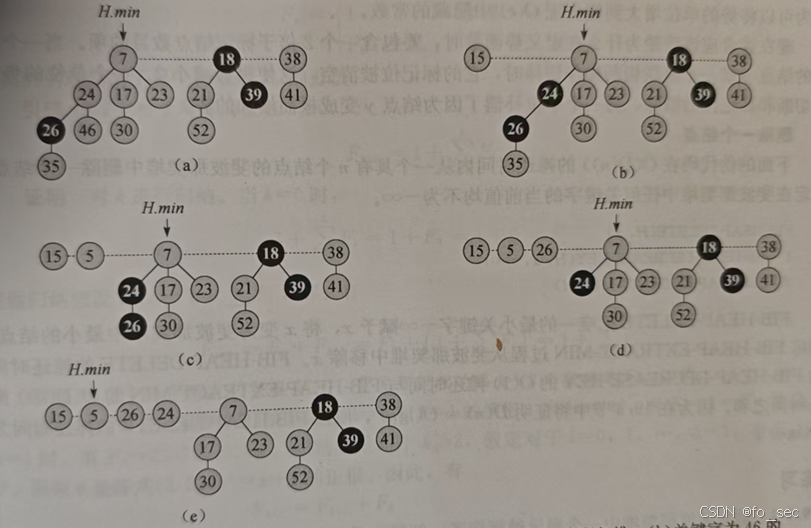




















 2321
2321

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








