文章全写在word了,着实是懒得再调整格式了orz
1.排序
稳定排序:稳定排序算法是指能够保持相等排序项的初始相对顺序的排序算法。如果两个对象相等,稳定排序算法会保留它们在输入集合中的顺序。相反,不稳定排序算法可能不会保留这种顺序。
稳定:冒泡,插入,归并,基数
不稳定:选择,快速,shell,堆
1.冒泡
可以理解为从尾到头确定每一位的未知,假如是从小到大,那么相邻两两比较,让较大的比较到后面去。每一轮通过冒泡都会确定最后一位数,所以第k轮只需要冒泡m-k次即可(因为后面的k位通过冒泡已经确定最大)
时间复杂度:O(n2)
伪代码:
For i=start to end:
For j=start+1(防止比较头空) to end-i:
if arr[j]<arr[j-1](前面的比后面的大)
switch(arr[j],arr[j-1])
2.归并
将一个数组分割成两部分,两部分排完序后再统一排序
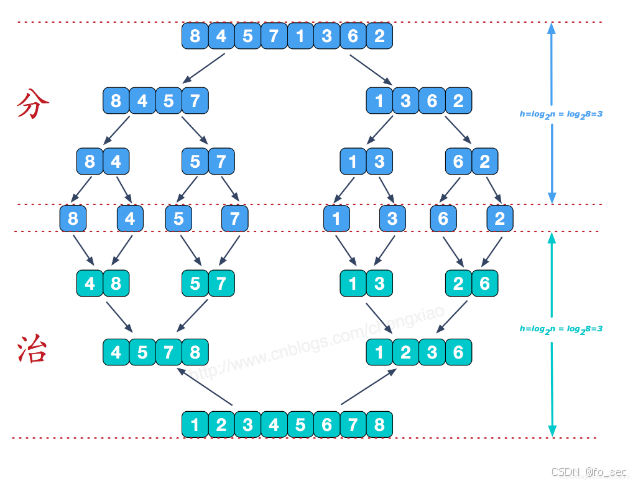
时间复杂度:O(nlogn)(仅次于快速排序)
3.堆排序(最优化的性质)
堆排序是基于使用最优化队列所形成的排序。由于最优化队列的堆顶必定是最大(最小),每次取出最大(最小即可)
时间复杂度:O(nlogn)
只需要注意的是每次取出后如何维护堆的最优化即可。
方法:向下过滤(详见动手学数据结构&算法导论),我们取出后可以将最后一个数放到根部,然后从根部开始向下过滤。此时,比较根部与左右,将其与左右最大的那一个互换,然后沿着互换的路径一路换下去直到其已经是最大的父节点or成为了叶节点未知。
伪代码:
MAX-HEAPIFY(A,i):
L=left
R=right
If l<A.heap-size and A[l]>A[i]
largest=L
else
largest=i
if r<A.heap-size and A[r]>A[largest]
largest=r
if largest!=i
exchange A[i] with A[largest]
MAX-HEAPIFY(A,largest)
当我们进行建堆的时候,只需要对每一个非叶子节点进行向下过滤即可。
伪代码:
BUILD-MAX-HEAP(A):
A.heap-size=A.length
for i = A.length/2(向下取整) downto 1
MAX-HEAPIFY(A,i)
4.快速排序
快速排序类似于分治排序,但是分治是直接中间分,这导致在合在一起的时候会大量重复比较。快速排序则取一个分治点,分治点左比其小,右比其大。
有两种选择方法,第一种是直接选最后,第二种是随机选(随机快速排序)。
此处介绍直接选最后。在选择分治点后的调整分治数列有两种方法:
(1)左右指针,定义left=begin,right=end.将left放入temp(分治点),则left点为空,right从end开始向左寻找直到找到一个小于temp的,将其放入left的空中,此时right为空,则left开始向右寻找直到找到比temp大的为止,将其放入right的空中,循环到left==right即全部区分完毕后temp放入剩下的空中。
伪代码:
Def PARTITION(A,p,r):
left=p,right=r
temp=A[r]
while left<right:
while left<right and A[left]<temp:
left++
exchange A[left] with A[right]
while right>left and A[right]>temp:
right++
exchange A[right] with A[left]
A[left]=temp
(2)快慢指针(算法导论)。定义fast与slow,当A[fast]<temp时,将A[++slow]与A[fast]交换。最后slow+1就是交换点。可以理解为slow在后面给fast兜比temp大的底。
伪代码:
Def PARTITION(A,p,r):
temp=A[r]
slow=p-1
for fast=p to r-1:
if A[fast]<temp
slow++
exchange A[slow] with A[fast]
exchange A[slow+1] with A[r]
return slow+1
快速排序时间复杂度:
最坏划分情况:Θn2,每次划分都是Θn。当完全有序时也是Θn2
最好划分情况:Θnlogn。是的快排是逼近小于,比Onlogn强
平衡划分:Onlogn。实际上平均来说划分坏情况会与划分好情况相互平衡,最终的结果相比其他排序会更逼近Onlogn
5.计数排序(桶排序ProMax)
核心思想是,加入在x前面有15个数,那么x就应该是第16位。
伪代码:
COUNTING-SORT(A,B,k):
let C[0..k] be a new array
for i=0 to k
C[i]=0
for j=1 to A.length
C[A[j]]++
for i=1 to k
C[i]=C[i]+C[i-1]
for j=A.length downto 1
B[C[A[j]]]=A[j]
C[A[j]]=C[A[j]]-1
其中,B是输出,C提供临时储存空间。
时间复杂度:Θ(k+n)![]() 。当k=O(n)
。当k=O(n)![]() 时,为Θ(n)
时,为Θ(n)![]()
6.基数排序
核心思想是从个位开始从小到大排序,然后是十位,百位……一直到全部位数排序完为止。其是通过最低有效位开始排序的。
伪代码:
RADIX-SORT(A,d):
for i=1 to d:
use a stable sort to sort array A on digit i
时间复杂度:计数排序时间复杂度较为难计算。算法导论指出其为线性时间排序,即理论上为Θ(n)。但是所舍去的常数项不同,故基数排序循环轮数少,但每一轮会消耗更多时间。当主存珍贵时,更倾向于快速排序。
7.桶排序
可以理解为漏斗hash,即:根据最高位位数定义0-9共计十个桶,再对下一位每个桶定义0-9共计十个桶。根据输入数字从头到尾开始确定它应该在哪个桶,确定桶里有几个数。
实际上,由于这样空间复杂度消耗过高,很多时候经过1-2次漏斗hash后转化为list,此后针对list进行排序。此时的list将会较短排序更快。
伪代码:
BUCKET-SORT(A):
n=A.length
let B[0..n-1] be a new empty array
for i=1 to n:
insert A[i] into list B[A[i] on digit 1]
for i=0 to n-1
sort list B[i] with insert sort
concatenate the list B[0]……B[n-1] together in order
时间复杂度:取决于碰撞程度,若全为桶无list则为O(n),最坏情况退化为O(nlogn)。相对的空间则会占用较大。
8.Shell排序
Shell排序本质上是对选择排序的改进版。其每次会相隔x个进行分组,在分组内进行排序,随后对x/2进行分组,重新排序,一直除2排序直到x为1为止。
伪代码:
d = A.length / 2
while d > 0
for i = 1 to d
for j = i + d to A.length by d
tmp = A[j]
k = j - d
while k > 0 and A[k] > tmp
A[k + d] = A[k]
k = k - d
A[k + d] = tmp
d = d / 2
时间复杂度为:O(n1.3-2),故相比快排较慢。中等数据集表现良好




















 5万+
5万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








