5.图论
1.建图：
建图有三种方法：
（1）邻接矩阵：对于n个点定义[n+1][n+1]（废弃头部0行0列）矩阵，面对pair{x,y}表示x到y，或者pair{pair{x,y},value}表示x到y且有权重value，则将[x][y]处设置为value大小，其余均设置为0或者infinity。
代码：
int arr[max][max]={0};
void build(pair<pair<int,int>,int> line)
{
for(auto& [[x,y],value]:line)
arr[x][y]=value;
}(2)邻接表：对于n个点定义n个list，其中第i个list表示第i个点中所链接的点。
代码：
std::array<std::vector<std::pair<int, int>>,max> arr;
void build(std::vector<std::pair<std::pair<int, int>,int>> line)
{
for (auto& [xy, value] : line)
{
auto& [x, y] = xy;
arr[x].push_back({ y,value });
}
}（若C++17以前不支持CTAD与结构化绑定，则push_back后改为make_pair，结构化绑定改为first second访问）
（3）链式向前星
前面的方法存在很大的弊端：使用邻接矩阵时，空间占用极大；使用邻接表时，访问效率较低。故存在链式向前星储存图标方法，可以在空间紧张时使用。
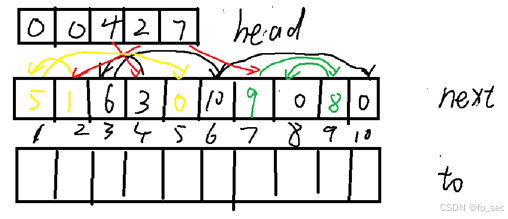
定义3个数组：
head[n+1]，n为点的数量
next[m+1]，m为边的数量
to[m+1],m为边的数量
cnt=1,cnt用于边进行编号。
一开始时，全部记为0。
当输入第一个边[4,3]时，cnt=1，故[4,3]为第一条边。则next[1]改为head[4]的数值=0，head[4]改为cnt++=1数值，用于记录点4有边1，to[1]改为第一条边的目的地3。而后加入[4,7]，cnt=2，故[4，7]为第二条边。next[2]改为head[4]的数值=1，表示第二条边的下一条边是第一条边。to[2]=7，head[4]改为cnt++=2的数值。
这种方式创造了一条伪链表。当我们访问4有哪些边时，从head访问找到第二条边，而第二条边可以通过next访问找到第一条边，从而知道4有哪些边。当链式追着访问到0，则表示访问完全了。
代码：
std::array<int, max> head { 0 };
std::array<int, max> next { 0 };
std::array<std::pair<int, int>, max> to{ std::make_pair(0,0)};
void build(std::vector<std::pair<std::pair<int, int>,int>> line)
{
int cnt = 1;
for (auto& [xy, value] : line)
{
auto& [x, y] = xy;
next[cnt] = head[x];
to[cnt] = { y,value };
head[x] = cnt++;
}
}注意：无向图中边长需要翻倍用来储存两条边
2.拓扑排序：如果存在一条从vi
到vj
的路径，那么排序中vj
在vi
后面。
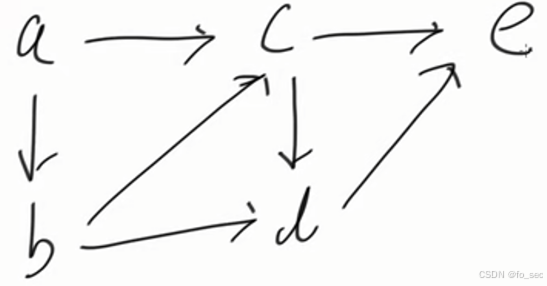
也就是说，我们要找一条通路，通路上后面的节点不允许有路通向前面，只准从前面走到后面，不准从后面走到前面。（比如大学课程，要学完前面才能学后面，不能学后面在学前面）
方法：每一次选一个入度为0的点放入queue中，并且擦除掉其边变成子图，重复选择直到图全被擦除完为止。一旦没有入度为0的边，那么则不存在拓扑排序。
在进行排序过程中可以创建一个入度数组用来维护入度。
使用拓扑排序进行树状dp：851. 喧闹和富有 - 力扣（LeetCode）
我们可以将方法一中的图的边全部反向，即如果 ai
比 bi
更有钱，我们从 ai
向 bi
连一条有向边。
此时，根据“在所有拥有的钱肯定不少于 person x 的人中，person y 是最不安静的人”，我们可以从最穷的往富有的进行dp，富有的里面最不安静的则是max（传上来的安静与自己的安静值）。
代码：
vector<int> loudAndRich(vector<vector<int>>& richer, vector<int>& quiet) {
int n=quiet.size();
vector<vector<int>> g(n);
vector<int> inDeg(n);
for(auto& r:richer){
g[r[0]].emplace_back(r[1]);
++inDeg[r[1]];
}
vector<int> ans(n);
iota(ans.begin(),ans.end(),0);
queue<int> q;
for(int i=0;i<n;++i)
if(inDeg[i]==0)
q.emplace(i);
while(!q.empty()){
int x=q.front();
q.pop();
for(int y:g[x]){
if(quiet[ans[x]]<quiet[ans[y]])
ans[y]=ans[x];
if(--inDeg[y]==0)
q.emplace(y);
}
}
return ans;
}2.最小生成树：
Kruscal算法：加边，每次加最小边
Prim算法：加点，每次加最小的点。编写prim可以有个优化：使用vector记录最小化堆（用于储存此时链接的边）进行快速的修改。
3.最短路径算法：
（1）Dijkstra算法：贪心算法典例。初始时将每个点标记为无穷大，随后从起点开始，将其所有连着的点加上连着的边的权重，然后从最小的点继续求其连着的点的权重进行更新。直到找完为止。
时间复杂度：O(m+n2)
实际上可以进行优先队列优化得到：O(m+nlogm)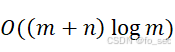
伪代码：
def Dijkstra(G, d, s):
for 循环n次:
u = 使d[u]最小的但还未被访问的顶点的标号
记u已被访问
for 从u出发能到达的所有顶点v:
if v未被访问 && 以u为中介点使s到顶点v的最短路径d[v]更优:
优化d[v]代码：（邻接表实现）
/*
函数名：dijkstra() 迪科斯彻最短路径算法
参数：vs：源点的索引;f：终点的索引;
pre[]：前驱数组,即pre[i]为从vs到i最短路径时,i前面那个顶点的索引
dist[]：距离数组，即dist[i]是vs到i的最短路径的长度
全局变量q：点的数量
功能：算出从源点下标vs到其余点最短路径,轨迹记录在pre[],距离记录在dist[]。
*/
void dijkstra( int vs, int prev[], int dist[],int f )
{
int i,j,k;
int min;
int tmp;
int flag[q]; // flag[i]=1表示"顶点vs"到"顶点i"的最短路径已成功获取。
/* 1. 初始化*/
for (i = 0; i < q; i++)
{
flag[i] = 0; // 顶点i的最短路径还没获取到。
prev[i] = vs; // 顶点i的前驱顶点为0。
dist[i] = martix[vs][i];// 顶点i的最短路径为vs到i的权。
}
flag[vs] = 1; // 对顶点vs自身进行初始化
dist[vs] = 0;
/* 2. 遍历q-1次，每次找出vs到另一个顶点的最短路径 */
for (i = 1; i < q ; i++){
/* 2.1 在未获取最短路径的顶点中，找到离vs最近的顶点k */
min = INF;
for ( j = 0; j < q ; j++){
if (flag[j]==0 && dist[j]<min)
//若从vs到顶点j距离小于min,而且从vs到j的最短路径还未获取。
{
min = dist[j];//改变最近距离
k = j;//记录j
}
}
/* 2.2 对刚刚已找到最短距离的顶点k进行标记判断 */
flag[k] = 1; // 标记顶点k,dist[k]已确定。
if(k==f) //判断k是否是终点索引,若是则退出
break;
/* 2.3 已知顶点k的最短路径后,更新未获取最短路径的顶点的最短路径和前驱顶点 */
for (j = 0; j < q ; j++) {
tmp = (martix[k][j]==INF ? INF : (min + martix[k][j])); // 防止溢出
if (flag[j] == 0 && (tmp < dist[j]) ) //若j还不是最短距离且从k到j距离比记录的距离短
{
//更新k的前驱和最短距离
prev[j] = k;
dist[j] = tmp;
}
}
}
}（2）A*算法：
相比于Dijskra算法，A*增加了从当前点岛重点的预估函数。在堆中根据：从源点出发到达当前点的距离+当前点到终点的预估距离来进行排序。而Dijskra算法只按照源点出发到达当前点的距离进行排序。
其余所有细节与Dijskra算法一致。
预估函数要求：当前点到终点的预估距离 <= 当前点到终点的真实最短距离
预估函数是一种吸引力；
1）合适的吸引力可以提升速度
2）吸引力过强会出现错误
常用预估终点：
曼哈顿距离，欧式距离，对角线距离
A*相比于Dijskra理论时间复杂度相同，但是常数项很小，故比其快多了。
但是Dijskra和A*无法处理有负边的情况，于是产生Floyd算法
（3）Floyd算法：
注意：任何最短路必须无负环，否则可以一直走环无穷小。
时间复杂度：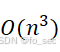
空间复杂度：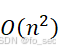
其核心在于针对每个
，是否存在一个
，使得
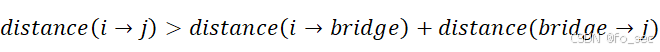
从而找到了一个更近的一个路径，此时将
更新。
代码：
void floyd(){
for(int bridge=0;bridge<n;bridge++){
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
if(distance[i][bridge]!=MAX_VALUE
&&distance[bridge][j]!=MAX_VALUE
&&distance[i][j]>distance[i][bridge]+distance[bridge][j])
distance[i][j]=distance[i][bridge]+distance[bridge][j];
}
}
}
}注意：一定不能把
循环嵌套顺序搞混！！！初始时将
与临接矩阵相同，其他全部赋无穷大。
然而由于其时间复杂度过高，提出Bellman-Ford算法进行优化。
（4）Bellman-Ford算法：
Bellman-Ford算法提出了松弛操作：
假设源点为A，从A到任意点F的最短距离为
，假设从P出发去某条边到达S，边权为W，如果发现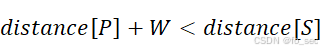
，则
可以变小，也就是从P出发到S进行了松弛操作。
Bellman-Ford过程：
每一轮考察每条边，每条边都进行松弛操作，那么若干点的
会变小。当某一轮发现无松弛操作时，则算法停止已经达到最优路径。
时间复杂度：
而松弛轮数必定<=n-1，因为最短路最多走过全部n个点。
Bellman-Ford还可以判断有无负环：如果从A点出发，到第n轮仍然能够进行松弛操作，那么则必定存在到A的负环。
代码如下：
for (j = 1; j <= n-1; ++j){ // 最多循环n-1轮（图退化为链表）
check = 0; // 用来标记在本轮松弛中数组dis是否发生更新
for (i = 1; i <= m; ++i)
{
if (dis[u[i]] != INF && dis[u[i]] + w[i] < dis[v[i]]){ // relax
dis[v[i]] = dis[u[i]] + w[i];
bak[v[i]] = u[i];
check = 1;
}
}
if (check == 0)
break;
}（5）SPFA优化：
Bellman-Ford太蠢了，每一轮都会考察所有的边。实际上只有上一轮进行了松弛情况下才可能会引起下一次的松弛。所以可以引入一个queue来维护“这一轮哪些节点进行了松弛操作”，下一轮只需要针对这些点的所有边考察松弛操作即可。
但是SPFA只优化常数时间，时间复杂度和Bellman-Ford相同。相比Bellman-Ford跑的还是快，但是根据数据量要谨慎使用。
番外：洪水填充算法
洪水填充算法指的是在一个地方搜索到后，接下来往四周进行搜索。例如寻岛问题：1254. 统计封闭岛屿的数目 - 力扣（LeetCode）
一片0中1表示陆地，问陆地连起来的岛屿有几座。那么找到一个1之后可以往四周进行dfs寻找直到找不到为止。
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
