数据结构：红黑树与AA树

3.红黑树

红黑树相比于AVL树，其牺牲了一定的平衡性，从而换取了相比较快的插入删除。

其需要满足以下四条性质：

1. 节点为红色或黑色
2. NIL 节点（空叶子节点）为黑色
3. 红色节点的子节点为黑色
4. 从根节点到 NIL 节点的每条路径上的黑色节点数量相同

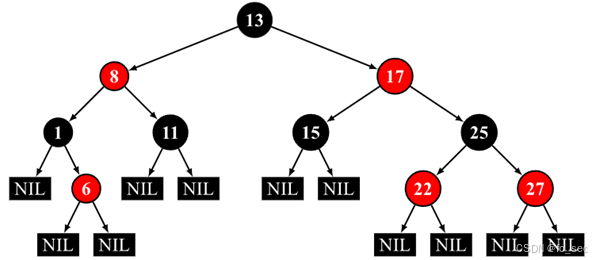
但是相对应的，插入和删除情况会较多。

讲调整前，先说明最核心一点：所有的调整都是为了调整不符合那一路的黑点！从而在确保符合性质那一路的黑点数量不变的情况下，左右无论那条路黑点都一样！不管用什么旋转染色都为了满足这一条！！！

插入：

（1）树为空，父节点为根节点且为黑节点，此时以满足不用管

（2）父节点为根节点且为红色，此时将其染黑则满足

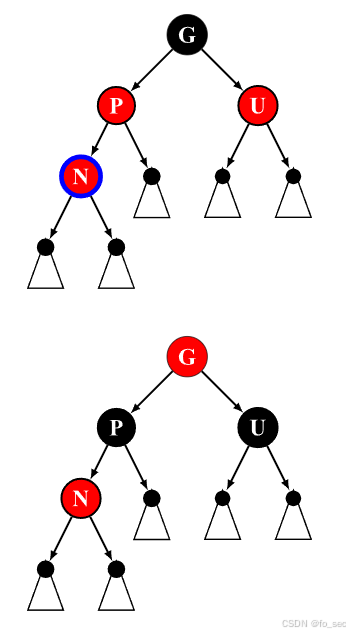（3）如右图，此时父节点P与叔节点U为红色。此时，由性质3，N的祖父节点G必定为黑色，否则两个红色相连。为了遵循红色的话，即左右在不变情况下保证红黑树左右黑色一样！！

最简单的方法：把P和U全部染黑，祖父节点G染红即可！

（4）如下图，此时N为内侧点，通过RR旋转转入case（5）进行调整即可

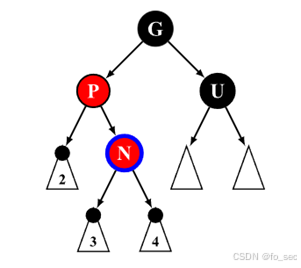
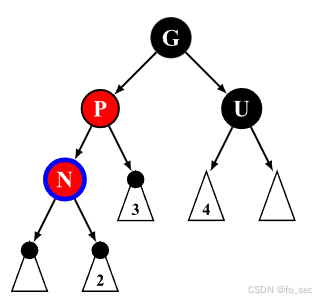（5）如右图，此时注意到G->U为双黑，G->P和G->P->N也是黑，唯一不满足的就是P和N是连红。

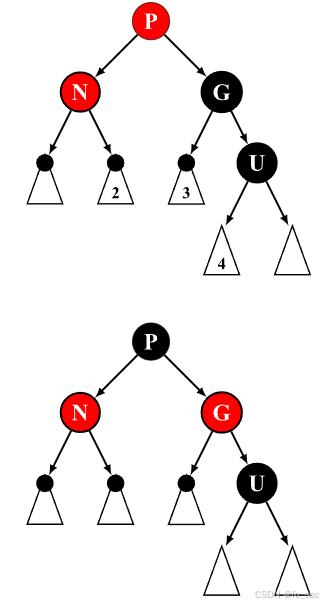我们最朴素的思想则是想办法把左侧红丢到右侧or想办法在左侧再插入黑。但是由于一旦动右侧黑则右侧变化否决红色警告，故只考虑第一条。

具体方法如左图。

我们想把一个红色节点丢过去，首先先要把一个节点丢过去。把G进行LL旋转使得P丢上root节点，此时我们对其重新染色，从而保证右路只多了一个红色节点。并且右路只少了一个红色节点。

删除：小时候看这集看哭了。将删除分为：删除与删除后的平衡调整两部分进行分别说明。

删除：（1）若待删除节点 N 既有左子节点又有右子节点，则需找到它的前驱或后继节点进行替换，则后续操作中只需要将后继节点删除即可。（和普通二叉查找树相同）

（2）待删除节点为叶子节点，若该节点为红色。若为黑色，删除后性质 4 被打破，需要重新进行维护。

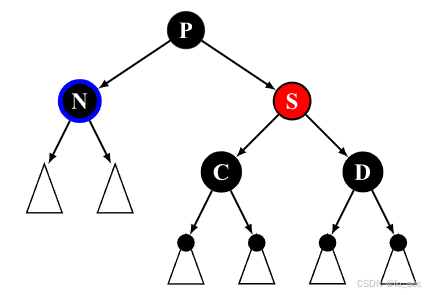
（3）待删除节点 N 有且仅有一个非 NIL 子节点，则子节点 S 一定为红色。因为如果子节点 S 为黑色，则 S 的黑深度和待删除结点的黑深度不同，违反性质 4。由于子节点 S 为红色，则待删除节点 N 为黑色，直接使用子节点 S 替代 N 并将其染黑后即可满足性质 4。

删除后的平衡调整：

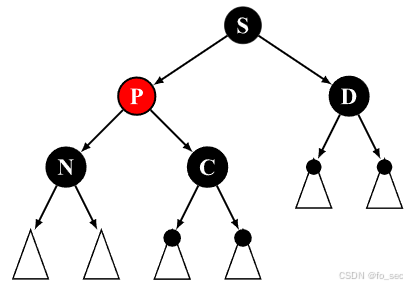（1）如右图，此时N为删除节点（已替换），注意到右侧的黑比左侧要深，所以需要想办法在左侧加入一个黑色。（不能影响右侧黑色深度）。

那么，我们注意到右侧有一个没用的红色，我们可以想办法把他丢到左侧染黑不就好了？丢过去了C怎么办？把C丢到左侧的右侧不就好了？（因为C在右侧最小相当于在左侧最大）。把S丢上去后将P染红即可。而后在针对N进行进一步的维护！

（2）兄弟节点 S 和侄节点 C, D 均为黑色，父节点 P 为红色。此时我们需要给左侧加一个黑色并且右侧不变，注意到直接将 S 染红，将 P 染黑即可满足性质 3 和 4。

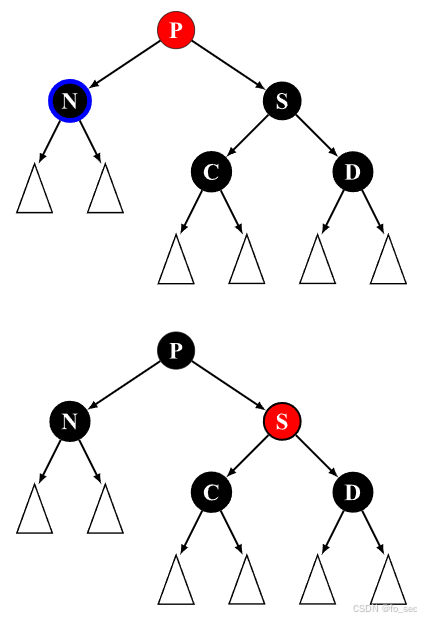
（3）兄弟节点 S，父节点 P 以及侄节点 C, D 均为黑色。

此时也无法通过一步操作同时满足性质 3 和 4，因此选择将 S 染红，优先满足局部性质 4 的成立，再递归维护 P 节点根据上部结构进行后续维护

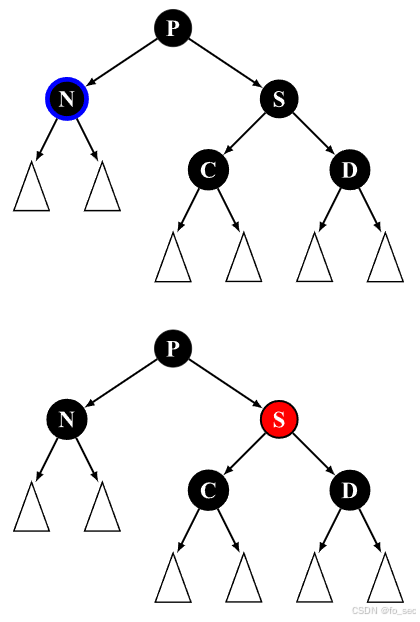
（4）兄弟节点是黑色，且与 N 同向的侄节点 C为红色，与 N 反向的侄节点 D为黑色，父节点既可为红色又可为黑色。

此时同样无法通过一步操作使其满足性质，因此优先选择将其转变为 Case 5 的状态利用后续 Case 5 的维护过程进行修正

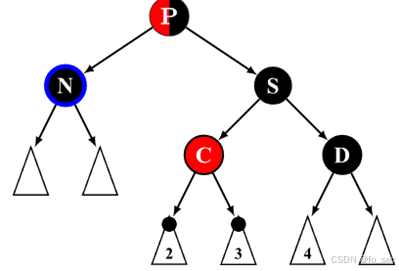
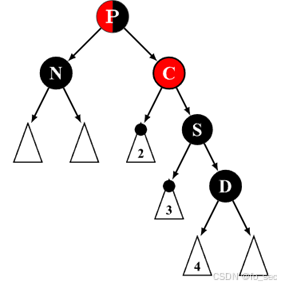
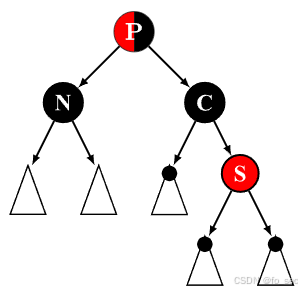
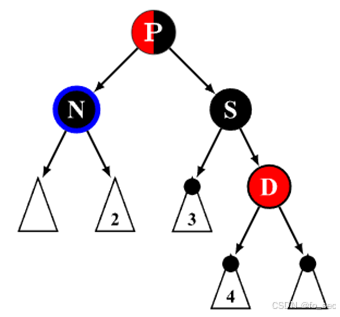
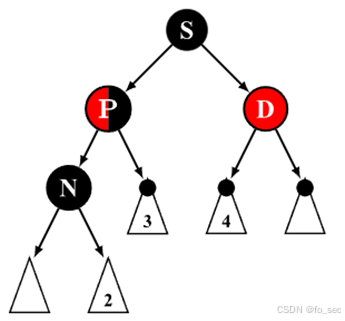
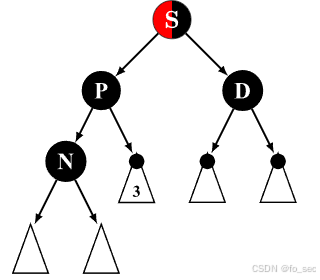
（5）兄弟节点是黑色，且节点 D 为红色，close nephew节点和父节点既可为红色又可为黑色。此时性质 4 无法满足，通过旋转操作使得黑色节点 S 变为该子树的根节点再进行染色即可满足性质 4。

左边少黑！转一个D过去给他不就好了！！！

4.AA Tree

AA Tree是红黑树的改进版，其在红黑树上添加了一条限制条件：即红色节点不能作为左孩子出现。

AA Tree相比红黑树，其所需要考虑的情况显著减少，同时其运行速度相比于红黑树有丝毫提升（但是红黑树存在多年已经被卷到一滴不剩了，所以调用库的红黑树反而可能会更快）。

此时，AA Tree不再用红黑来平衡，而是用level来平衡。其应当满足以下条件：

1、每个叶节点的 level 是 1。

2、每个左孩子的 level 是其父节点的 level 减 1。

3、每个右孩子的 level 等于其父节点的 level 或等于其父节点的 level 减 1。

4、每个右孙子的 level 严格小于其祖父节点的 level。

5、每个 level 大于 1 的节点有两个孩子。

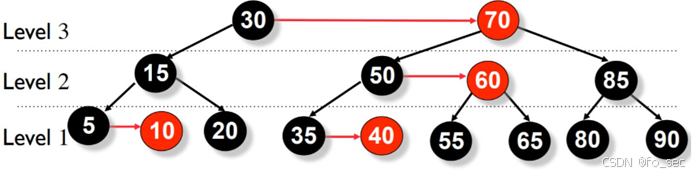
子节点的 level 等于父节点的 level 的链接被称为 水平链接，类似于红黑树中的红链接。允许单独的右水平链接，但不允许连续的右水平链接；不允许左水平链接。

AA Tree只有两种操作：skew（斜化）和split（分裂）

（1）skew：出现向左的水平方向链（连续两个向左的孩子属于同一 level）如下图，此时只需要进行斜化（把向左转成向右即可）

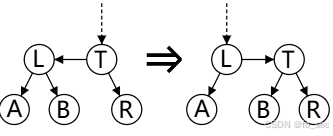
（2）split：出现连续向右的水平方向链（连续三个向右的孩子属于同一 level，节点 R 和节点 X 都是红色节点）。

插入：

伪代码实现：

def insert(root,add):

       if root equal NULL:
              set root as add

       else if add->key smaller than root->key

              insert(root->left,add)

       else if add->key bigger than root->key

              insert(root->right,add)

       else if //如果不允许重复，在每一level上进行skew和split

       skew(root)

       split(root)

删除：删除过程与其他二叉平衡树类似，首先将内部节点的删除转换为叶子节点的删除。具体方法是将内部节点与它最接近的前驱或后继节点替换。由于 AA 树的所有 level 大于 1 的节点都有两个子节点，前驱或后继节点将位于 level 1，删除 level 1 的节点较为简单。

伪代码：

//to balance the tree

if root->left(or right)->level smaller than root->level-1

       if root->right->level bigger than –-root->level

              set root->right->level equal to root->level

       skew(root)

       skew(root->right)

       skew(root->right->right)

       split(root)

       split(root->right)                                                                                                      

AA 树的性能与红黑树的性能相当。尽管 AA 树进行的旋转操作比红黑树多，但 AA 树的算法更简单，最终导致相近的性能。红黑树的性能在各种情况下更加一致，而 AA 树往往更扁平，这使 AA 树有稍快的搜索速度。