3.2.4 More Circuit
3.2.4.1 Rule90
Rule90是一道根据一些有趣规则生成一维序列的题目
规则很简单,一维序列中有0和1两种状态
下表更详细地给出了跳变的规则,(可以视为状态转移表),元素下一个状态可以视作输出,输入为元素本身的状态与相应两个相邻元素的当前状态。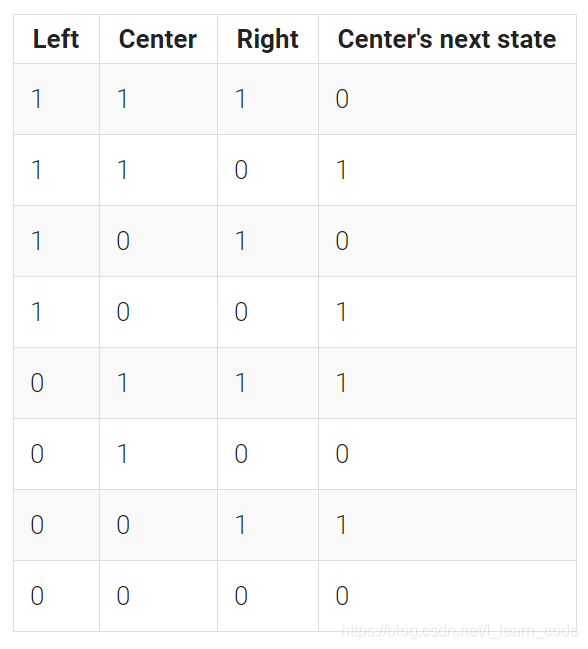
对于需要实现的电路,创建一个拥有 512 个元素的序列 q[511:0],每个时钟周期按照上述规则变换。load 信号有效时,序列更新 data 信号值为初始值。另外假设所有边界的值为 0 (q[-1] 以及 q[512])
从真值表中不难看出,center的下一个状态,是由center左右两个状态异或而得
module top_module(
input clk,
input load,
input [511:0] data,
output [511:0] q );
integer i;
always @ (posedge clk) begin
if(load) begin
q <= data;
end
else begin
q[0] <= q[1] ^ 0;
q[511] <= q[510] ^ 0;
for(i = 1; i < 511; i++) begin
q[i] <= q[i-1] ^ q[i+1];
end
end
end
endmodule
3.2.4.2 Rule110
在每个时钟上升沿,元素状态发生改变。在rule110中,元素的下一个状态不仅与当前状态有关,还与当前状态两边的状态有关。
下图给出了更详细的状态变化关系:
在这个电路中,要求创建一个由512的元素组成的系统q[511:0],规定每个时钟上升沿前进一步,load有效是,将所有状态赋值为data[51:0],且假设q[-1]和q[512]都是0
module top_module(
input clk,
input load,
input [511:0] data,
output [511:0] q
);
wire [511:0] left;
wire [511:0] right;
assign right = {q[510:0],1'b0};
assign left = {1'b0,q[511:1]};
always @ (posedge clk) begin
if(load) begin
q <= data;
end
else begin
q <= (q ^ right) | (q & (~left));
end
end
endmodule
从真值表中可以看出,输出out = (center ^ right) | (center & (~left))
在开始时,先设定两个变量来存储left和right,在load = 0时,直接套用逻辑表达式即可
3.2.4.3 Conway’s Game of Life 16×16
game是在二维网格上进行的,每个元素1有效,0无效
规则如下:
时钟上升沿时,元素的下一个状态会根据与其相邻的元素为1的个数进行变化:
- 0-1 : 元素变为
0 - 2 : 状态步变
- 3 : 元素变为
1 - 4+ : 元素变为
0
二维矩阵可以是无限的,为了方便做题,本题矩阵设定为16×16
本题对二维矩阵做了环形处理,例如,元素(0,0)旁边的元素分别为 (15,1)、(15,0)、(15,15)、(0,1)、(0,15)、(1,1)、(1,0)和(1,15)。
16×16矩阵由一个长度为256的向量表示,其中q[15:0]是第0行,q[31:16]是第一行
- load : 将
data数据传给q - q:每个时钟周期,更新一次状态
没有敲出来,放弃了~~~~~~~~~~~~~~~~~~~~~~~





 本文介绍了Rule90和Rule110两种一维序列生成电路的设计,以及Conway's Game of Life在16x16矩阵上的实现。在Rule90电路中,每个元素的状态由其两侧元素异或决定;Rule110电路中,状态更新考虑当前及两侧元素。而对于Conway's Game of Life,元素状态依据相邻元素数量变化,遵循特定规则。电路均在每个时钟上升沿更新状态,并支持在load信号有效时初始化序列。
本文介绍了Rule90和Rule110两种一维序列生成电路的设计,以及Conway's Game of Life在16x16矩阵上的实现。在Rule90电路中,每个元素的状态由其两侧元素异或决定;Rule110电路中,状态更新考虑当前及两侧元素。而对于Conway's Game of Life,元素状态依据相邻元素数量变化,遵循特定规则。电路均在每个时钟上升沿更新状态,并支持在load信号有效时初始化序列。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








