最短路径
我们做公交车或者地铁时,总要考虑从A到B站点如何乘坐更快,换句话说就是要找到交通网图选择的两点间的最短距离。对于网图来说,最短路径,是指两顶点之间经过的边上权值之和最少的路径,并且我们称路径上的第一个顶点是源点,最后一个顶点是终点。
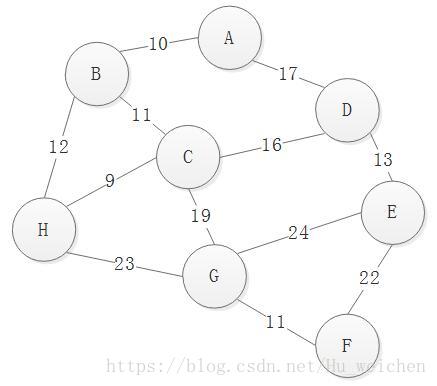
图1图1
迪杰斯特拉( Dijkstra ) 算法
迪杰斯特拉( Dijkstra ) 算法是从源点开始一步步求出它们之间顶点的最短路径,过程中都是基于已经求出的最短路径的基础上,求得更远顶点的最短路径,最终得到你要的结果。我们来看下相关代码:
#include <vector>
#include <iostream>
using namespace std;
#define INFINITY 65535
class Graph
{
public:
Graph();
~Graph();
void CreateGraph();//创建图
void DFSTraverse();//深度遍历操作
void ShortestPath_Dijkstra(int v0);//Dijkstra算法
vector<int> Pathmatirx;//最短路径下标数组
vector<int> ShortPathTable;//各点最短路径的权值和
vector<char> vexs; //顶点表
private:
void DFS(int i);//深度遍历递归数组
vector<vector<int>>arc;//邻接矩阵
vector<bool>visited;//访问标志数组
int numVertexes, numEdges;
};
#include "Graph.h"
Graph::Graph()
{
}
Graph::~Graph()
{
}
void Graph::CreateGraph()
{
cout << "输入顶点数和边数:" << endl;
cin >> numVertexes >> numEdges;
cout << "输入顶点:" << endl;
int i, j, w;
char ch;
for (i = 0; i < numVertexes; i++)
{
cin >> ch;
vexs.push_back(ch);
}
arc.resize(numVertexes, vector<int>(numVertexes));
for (i = 0; i < numVertexes; i++) //初始化邻接矩阵
for (j = 0; j < numVertexes; j++)
{
if (i != j)arc[i][j] = INFINITY;
else arc[i][j] = 0;
}
cout << "输入边( vi ,vj)上的下标i,下标j,和权w :" << endl;
for (int k = 0; k < numEdges; k++)
{
cin >> i >> j >> w;
arc[i][j] = arc[j][i] = w;
}
}
void Graph::DFSTraverse()//深度遍历操作
{
for (int i = 0; i < numVertexes; i++)
visited.push_back(false);
for (int i = 0; i < numVertexes; i++)
if (!visited[i])
DFS(i);
cout << endl;
}
void Graph::DFS(int i)//深度遍历递归数组
{
visited[i] = true;
cout << vexs[i] << " ";
for (int j = 0; j < numVertexes; j++)
if ((arc[i][j] != 0 && arc[i][j] != INFINITY) && !visited[j])
DFS(j);
}
void Graph::ShortestPath_Dijkstra(int v0)//Dijkstra算法
{
int min,k;
vector<int> final;//final[w]=1 表示求得顶点Vo至Vw的最短路径
for (int i = 0; i < numVertexes; i++)
{
final.push_back(0);
Pathmatirx.push_back(v0);
ShortPathTable.push_back(arc[v0][i]);
}
ShortPathTable[v0] = 0;
final[v0] = 1;
for (int i = 1; i < numVertexes; i++)
{
min = INFINITY;
for (int j = 0; j < numVertexes; j++)
{
if (!final[j] && ShortPathTable[j] < min)
{
k = j;
min = ShortPathTable[j];
}
}
final[k] = 1;
for (int j = 0; j < numVertexes; j++)
{
if (!final[j] && (min + arc[k][j] < ShortPathTable[j]))
{
ShortPathTable[j] = min + arc[k][j];
Pathmatirx[j] = k;
}
}
}
}#include <iostream>
#include<stack>
#include "Graph.h"
using namespace std;
int main()
{
Graph G;
G.CreateGraph();
int s, e;
stack<int> path;
cout << "输入起点和终点结点的下标:" << endl;
cin >> s >> e;
G.ShortestPath_Dijkstra(s);
cout << "最短路径:" << endl;
for (; s != e; e = G.Pathmatirx[e])
{
path.push(e);
}
path.push(e);
int size = path.size();
for (int i = 0; i < size-1; i++)
{
cout << G.vexs[path.top()] << "->";
path.pop();
}
cout << G.vexs[path.top()] << endl;
path.pop();
system("pause");
return 0;
}
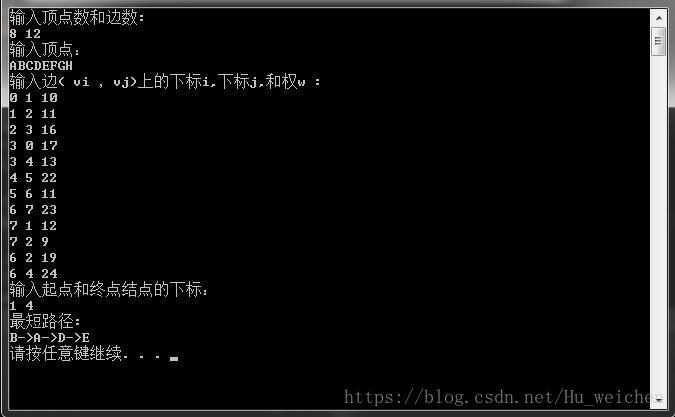
我们把图1中的网图输入,在VS下运行结果如下:
弗洛伊德( Floyd )算法
迪杰斯特拉( Dijkstra ) 算法计算的是一个点到其他点的最短路径。当面临需要求所有顶点至所有顶点的最短路径问题时,可以采用弗洛伊德( Floyd )算法。其代码如下:
#include <vector>
#include <iostream>
using namespace std;
#define INF 65535
class Graph
{
public:
Graph();
~Graph();
void CreateGraph();//创建图
void DFSTraverse();//深度遍历操作
void ShortestPath_Floyd();//Floyd算法
vector< vector<int>>Pathmatirxm;
vector< vector<int>>ShortPathTable;
vector<char> vexs; //顶点表
private:
void DFS(int i);//深度遍历递归数组
vector<vector<int>>arc;//邻接矩阵
vector<bool>visited;//访问标志数组
int numVertexes, numEdges;
};#include "Graph.h"
Graph::Graph()
{
}
Graph::~Graph()
{
}
void Graph::CreateGraph()
{
cout << "输入顶点数和边数:" << endl;
cin >> numVertexes >> numEdges;
cout << "输入顶点:" << endl;
int i, j, w;
char ch;
for (i = 0; i < numVertexes; i++)
{
cin >> ch;
vexs.push_back(ch);
}
arc.resize(numVertexes, vector<int>(numVertexes));
for (i = 0; i < numVertexes; i++) //初始化邻接矩阵
for (j = 0; j < numVertexes; j++)
{
if (i != j)arc[i][j] = INF;
else arc[i][j] = 0;
}
cout << "输入边( vi ,vj)上的下标i,下标j,和权w :" << endl;
for (int k = 0; k < numEdges; k++)
{
cin >> i >> j >> w;
arc[i][j] = arc[j][i] = w;
}
}
void Graph::DFSTraverse()//深度遍历操作
{
for (int i = 0; i < numVertexes; i++)
visited.push_back(false);
for (int i = 0; i < numVertexes; i++)
if (!visited[i])
DFS(i);
cout << endl;
}
void Graph::DFS(int i)//深度遍历递归数组
{
visited[i] = true;
cout << vexs[i] << " ";
for (int j = 0; j < numVertexes; j++)
if ((arc[i][j] != 0 && arc[i][j] != INF) && !visited[j])
DFS(j);
}
void Graph::ShortestPath_Floyd()//Floyd算法
{
Pathmatirxm.resize(numVertexes, vector<int>(numVertexes));
ShortPathTable.resize(numVertexes, vector<int>(numVertexes));
for (int i = 0; i < numVertexes; i++)
{
for (int j = 0; j < numVertexes; j++)
{
ShortPathTable[i][j] = arc[i][j];
Pathmatirxm[i][j] = j;
}
}
for (int i = 0; i < numVertexes; i++)
{
for (int j = 0; j < numVertexes; j++)
{
for (int k = 0; k < numVertexes; k++)
{
if (ShortPathTable[j][k] > ShortPathTable[j][i] + ShortPathTable[i][k])
{
ShortPathTable[j][k] = ShortPathTable[j][i] + ShortPathTable[i][k];
Pathmatirxm[j][k] = Pathmatirxm[j][i];
}
}
}
}
}#include <iostream>
#include "Graph.h"
using namespace std;
int main()
{
Graph G;
int s, e;
G.CreateGraph();
G.ShortestPath_Floyd();
cout << "输入起点和终点结点的下标:" << endl;
cin >> s >> e;
cout << G.vexs[s];
while (s != e)
{
s = G.Pathmatirxm[s][e];
cout << "->" << G.vexs[s];
}
cout << endl;
system("pause");
return 0;
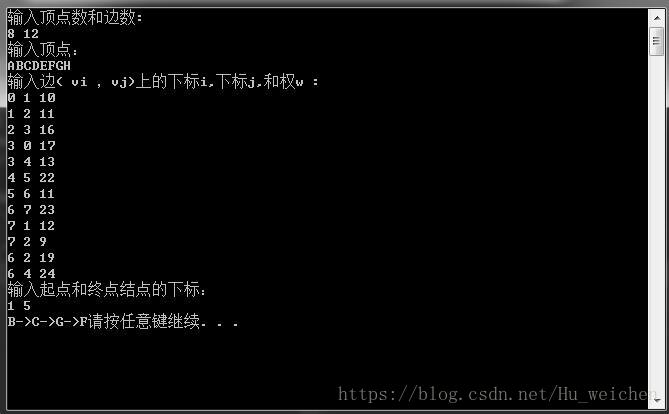
}我们把图1中的网图输入,在VS下运行结果如下:






 本文介绍了两种经典的最短路径算法——迪杰斯特拉算法和弗洛伊德算法,并提供了详细的代码实现。迪杰斯特拉算法适用于求解单一源点到其他各点的最短路径,而弗洛伊德算法则能解决任意两点之间的最短路径问题。
本文介绍了两种经典的最短路径算法——迪杰斯特拉算法和弗洛伊德算法,并提供了详细的代码实现。迪杰斯特拉算法适用于求解单一源点到其他各点的最短路径,而弗洛伊德算法则能解决任意两点之间的最短路径问题。

















 1677
1677

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










