- 三种不同的模型可视化方法:推荐torchinfo打印summary+权重分布可视化
- 进度条功能:手动和自动写法,让打印结果更加美观
- 推理的写法:评估模式
作业:调整模型定义时的超参数,对比下效果。
一、模型结构可视化
深度学习的重要思想:任务目标的量化(明确优化方向)和模型结构的可计算性(模型的复杂度)
1.1 意义
使用神经网络,从输入数据到输出结果,但在这之间的过程难以解释。因此需要使用相关的工具将结构进行可视化,用途举例如下:
- 验证模型结构是否正确:层次;
- 检查参数与计算量:每层输出的形状,参数数量,计算量;过拟合,资源规划
- 模型压缩与优化:剪枝;量化
1.2 方法
关于层可视化工具,介绍了三个方法。
nn.model 自带方法
可以选择直接打印model,可以得到输出模型的结构,包括各个层的名称及参数信息

另外,可以采用model.named_parameters()获取模型中可训练参数(比如权重和偏置)的迭代器(可遍历),每次迭代产生二元数组(name: str, param: torch.nn.Parameter):
- name:参数在模型中的完整命名路径(string),如'fc1.weight'
- param:对应的torch.nn.Parameter对象(带梯度的张量),直接转换为numpy数组会报错
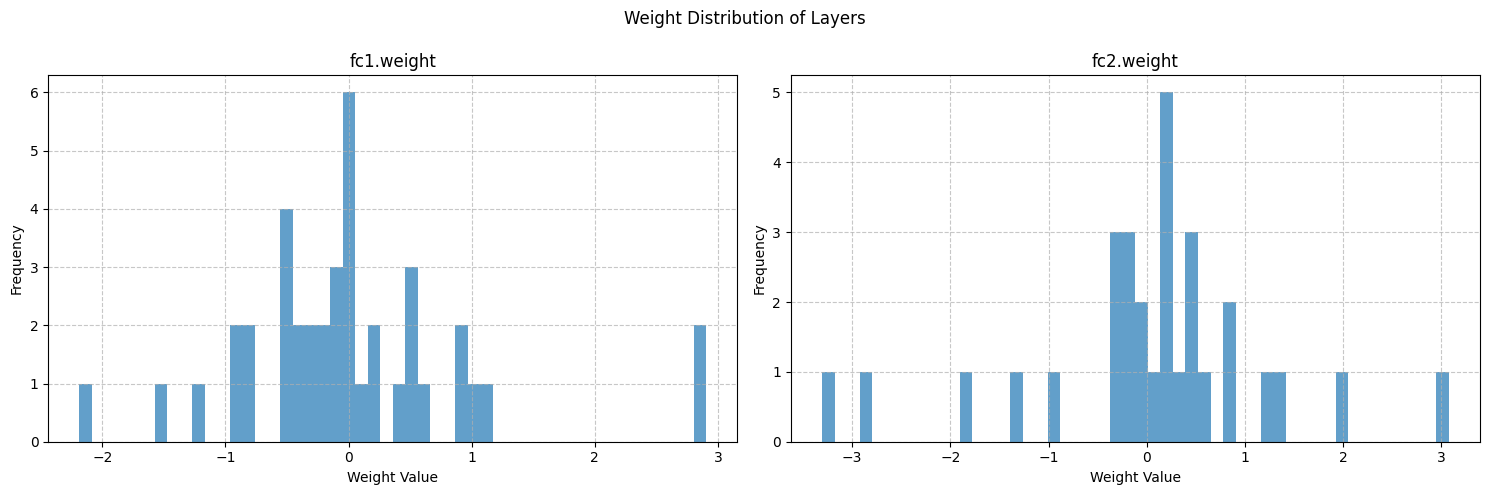
进一步地,将权重转换为Numpy数组,得到输入层和输出层中的weight分布情况:
# 可视化权重分布
weights = {}
for name,param in model.named_parameters():
if 'weight' in name:
weights[name] = param.detach().cpu().numpy()
print(weights)
fig,axes = plt.subplots(1,len(weights),figsize=(12,8))
fig.suptitle('Weight Distribution of Layers')
for i,(name,weight) in enumerate(weights.items()):
weight_flatten = weight.flatten()
axes[i].hist(weight_flatten,bins=50,alpha=0.7)
axes[i].set_title(name)
axes[i].set_xlabel('Weight Value')
axes[i].set_ylabel('Frequency')
axes[i].grid(True, linestyle='--', alpha=0.7)
plt.show()
# 计算并打印每层权重的统计信息
print("\n=== 权重统计信息 ===")
for name, weights in weight_data.items():
mean = np.mean(weights)
std = np.std(weights)
min_val = np.min(weights)
max_val = np.max(weights)
print(f"{name}:")
print(f" 均值: {mean:.6f}")
print(f" 标准差: {std:.6f}")
print(f" 最小值: {min_val:.6f}")
print(f" 最大值: {max_val:.6f}")
print("-" * 30)torchsummary库中的summary方法
from torchsummary import summary
# 打印模型摘要,可以放置在模型定义后面
summary(model, input_size=(4,))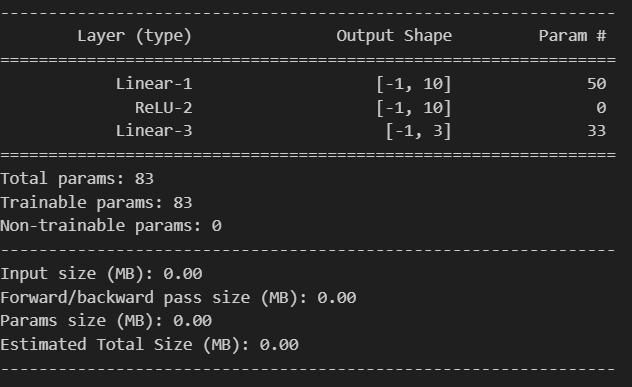
能够快速查看神经网络结构、参数量和计算流程,信息说明:
- 第一部分:在Output Shape中展示该层输出张量的形状,其中-1表示batch_size(动态值,由输入决定);Param #表示该层可训练参数数量
- 第二部分:参数量,总参数83=(4*10+10)+(10*3+3)
- 第三部分:内存估算,在大模型中更有意义
关于summary函数的核心逻辑:
- 创建一个与 input_size 形状匹配的虚拟输入张量(通常填充零)
- 将虚拟输入传递给模型,执行一次前向传播(但不计算梯度)
- 记录每一层的输入和输出形状,以及参数数量
- 生成可读的摘要报告
注意:input_size()不传入batch_size。

torchinfo库中的summary方法
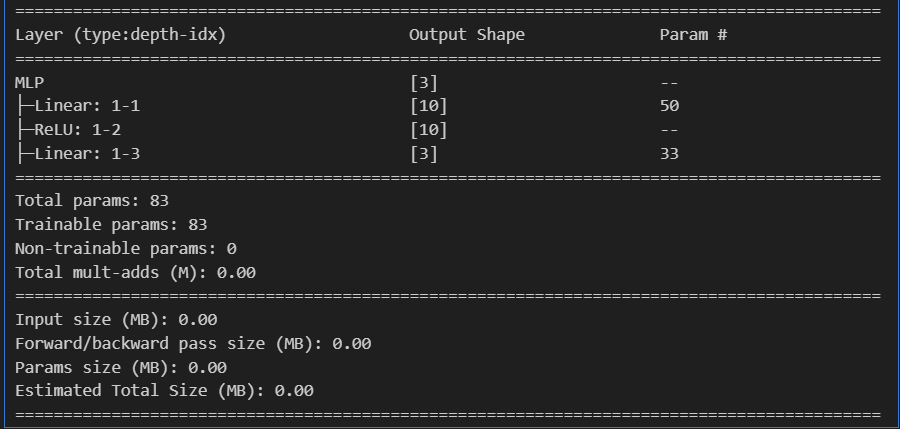
from torchinfo import summary
summary(model, input_size=(4, ))提供的信息比torsummary更全,算是它的升级版。
二、进度条功能
tqdm库,适合在循环中观察进度。核心逻辑如下:
- 创建进度条对象,并传入总迭代次数。一般用"with as"结构,结束后自动销毁,保证资源释放
- 更新进度条:使用pbar.update(n)增加前进步数(手动更新);进度条传入可迭代对象,自动更新
2.1 手动更新
# 进度条——手动更新
from tqdm import tqdm
import time
with tqdm(total=10, desc='下载文件',unit="个") as pbar:
for i in range(5):
time.sleep(0.5)
pbar.update(2)
此外,可以调整参数。还可以使用set_postfix方法在进度条右侧显示实时数据(如当前循环的数值、计算结果等):
# 计算1+2+..+10的进度条
from tqdm import tqdm
import time
total = 0
with tqdm(total=100,desc='计算总和') as pbar:
for i in range(1,11):
time.sleep(0.3)
total += i
pbar.update(10)
# 用tqdm的set_postfix方法在进度条右侧显示实时数据(如当前循环的数值、计算结果等)
pbar.set_postfix({"当前总和": total})
![]()
2.2 自动更新
使用可迭代对象,完成自动更新,无需手动update。
# 进度条——自动更新
from tqdm import tqdm
for i in tqdm(range(10),desc='处理任务',unit='epoch'):
time.sleep(0.5)在循环训练中加入进度条(手动更新):
# 循环训练
epoch_num = 20000
losses = []
epoch_list = []
start_time = time.time() # 记录开始时间
#加入进度条pbar
with tqdm(total=epoch_num,desc='训练进度',unit='epoch') as pbar:
for epoch in range(epoch_num):
# 基本流程
output = model(X_train)
loss = criterion(output,y_train)
optimiser.zero_grad()
loss.backward()
optimiser.step()
# 记录
if (epoch + 1) % 200 == 0:
losses.append(loss)
epoch_list.append(epoch + 1)
# 更新进度条的描述信息
pbar.set_postfix({'Loss': f'{loss.item():.4f}'})
#更新进度条
if (epoch + 1) % 1000 == 0:
pbar.update(1000)
# 更改训练轮数,也能确保进度条达到100%
if pbar.n < epoch_num:
pbar.update(epoch_num - pbar.n) # 计算剩余的进度并更新
time_all = time.time() - start_time # 计算训练时间
print(f'Training time: {time_all:.2f} seconds')三、模型的推理
在之前的机器学习过程中,训练后需要预测并借助评估指标得到模型训练效果。在大模型中,测试就是推理,即将数据输入到训练好的模型中。

使用model.eval()进入评估模式,在评估时要注意禁用与训练过程相关的操作,比如梯度计算(减少内存占用,提升性能)、参数更新等。
然后测试、获取最大概率的索引作为结果,与实际值比较,得到准确度。
注意:
- outputs:tensor类型,每一行是一个样本,每一行有3个值,分别是属于3个类别的概率,取最大值的下标就是预测的类别
- torch.max():返回2个值,分别是最大值和对应索引,dim=1是在第1维度(行)上找最大值,_ 是Python的约定,表示忽略这个返回值,所以这个写法是找到每一行最大值的下标
- 手动计算准确率:之所以不用sklearn的accuracy_score函数,是因为这个函数是在CPU上运行的,需要将数据转移到CPU上,这样会慢一些
# 模型评估
model.eval() # 设置模型为评估模式
with torch.no_grad(): # torch.no_grad()的作用是禁用梯度计算,可以提高模型推理速度
outputs = model(X_test) # 输入测试集,返回预测结果,Tensor形式
# torch.max(outputs, 1)返回每行的最大值和对应的索引
_, predictions = torch.max(outputs,dim=1) # dim=1为按行,dim=0为按列
# predicted == y_test判断预测值和真实值是否相等,返回一个tensor,1表示相等,0表示不等,然后求和,再除以y_test.size(0)得到准确率
correct_num = (predictions == y_test).sum().item() # 数据是tensor,所以用item()方法将tensor转化为Python的标量(int)
accuracy = correct_num / y_test.size(0) # size(0)获取第0维的长度,即样本数量
print('测试集的准确度:{:.2f}%'.format(accuracy*100))
四、作业
作业:调整模型定义时的超参数,对比下效果。
(1)改变隐藏层大小,[5,10,20,50,100],感觉准确率没提升,均为96.67%左右。
(2)改变激活函数类型:relu\sigmoid\tanh,hidden_size=10,准确率没变化
(3)隐藏层的层数改变,[1,2,3,4],2-4层时准确率为100%,但是随着层数的增加,训练的时间成本也有所增加。
# 修改后的模型建构 - 支持多层隐藏层
class MLP(nn.Module):
def __init__(self, hidden_layers=1, hidden_size=10):
"""
hidden_layers: 隐藏层的数量
hidden_size: 每个隐藏层的神经元数量
"""
super(MLP, self).__init__()
self.layers = nn.ModuleList()
# 输入层到第一个隐藏层
self.layers.append(nn.Linear(4, hidden_size))
self.layers.append(nn.ReLU())
# 添加额外的隐藏层
for i in range(hidden_layers - 1):
self.layers.append(nn.Linear(hidden_size, hidden_size))
self.layers.append(nn.ReLU())
# 输出层
self.layers.append(nn.Linear(hidden_size, 3))
def forward(self, x):
for layer in self.layers:
x = layer(x)
return x
# 在这里调整隐藏层数量
hidden_layer_counts = [1, 2, 3, 4] # 测试不同的隐藏层数量
hidden_size = 10 # 每层的神经元数量
results = [] # 存储每次结果:准确率,损失值等
for layer_count in hidden_layer_counts:
print(f"\n=== 训练 {layer_count} 层隐藏层的模型 ===")
# 创建模型
model = MLP(hidden_layers=layer_count, hidden_size=hidden_size).to(device)
# 后续代码放入循环即可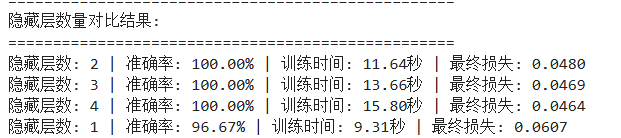
# 绘制损失曲线对比
plt.figure(figsize=(12, 8))
for result in results:
plt.plot(result['epochs'], result['losses'], label=f'{result["layers"]}', linewidth=2)
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.title('The Loss curve of different hidden layers')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()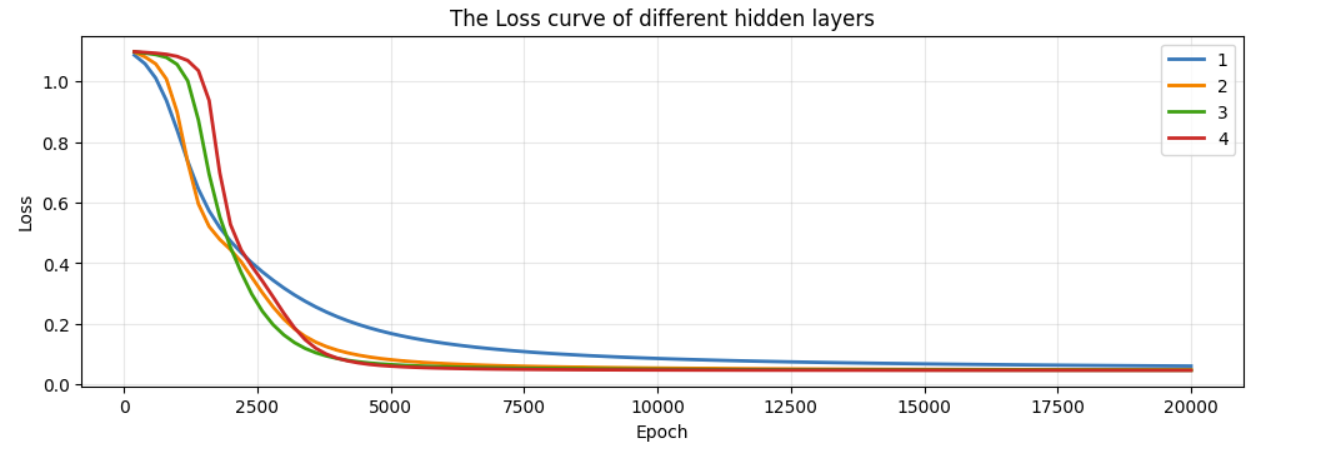






















 1249
1249

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








