- PyTorch和cuda的安装
- 查看显卡信息的命令行命令(cmd中使用)
- cuda的检查
- 简单神经网络的流程
关于环境配置
虽然本次为CPU版本,但是考虑电脑显卡配置和后续使用,选择使用AutoDL云服务器。本次选用的版本:
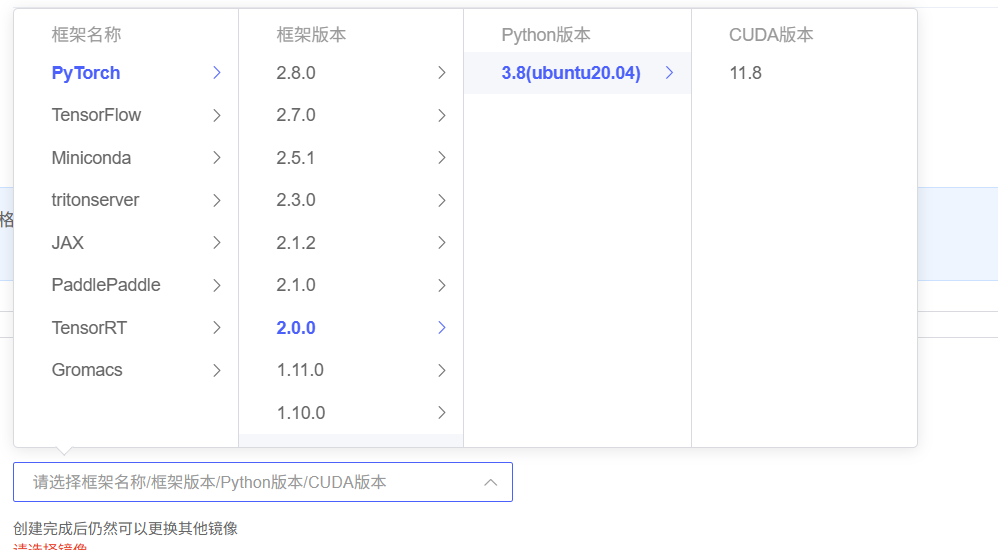
对于英伟达的显卡,可以在命令行中输入“nvidia-smi”查看显卡信息,得到新卡在目前驱动下最高支持的cuda版本以及显存大小。
cuda的可用性检查,得到可用设备数量、设备名称、版本等信息。后续可以复用代码,检查是否有pytorch及cuda相关信息,
import torch
# 检查CUDA是否可用
if torch.cuda.is_available():
print("CUDA可用!")
# 获取可用的CUDA设备数量
device_count = torch.cuda.device_count()
print(f"可用的CUDA设备数量: {device_count}")
# 获取当前使用的CUDA设备索引
current_device = torch.cuda.current_device()
print(f"当前使用的CUDA设备索引: {current_device}")
# 获取当前CUDA设备的名称
device_name = torch.cuda.get_device_name(current_device)
print(f"当前CUDA设备的名称: {device_name}")
# 获取CUDA版本
cuda_version = torch.version.cuda
print(f"CUDA版本: {cuda_version}")
# 查看cuDNN版本(如果可用)
print("cuDNN版本:", torch.backends.cudnn.version())
else:
print("CUDA不可用。")Multilayer Perceptron基础知识
之前没有学习过深度学习,简单了解一下多层感知机(MLP)的基础知识,学习视频:
【深度学习】感知机,神经网络,反向传播算法,梯度下降法等,用人话讲一些深度学习最简单最基础的内容
神经网络的概念
神经网络是一种能自动从数据中学习特征和规律的模型,通过多层“神经元”的组合,实现对复杂问题的建模。在传统机器学习中,特征(输入变量)通常需要人工设计或选择;而在神经网络中,它会自动从原始数据中“学习”出有用的特征,然后做出预测。
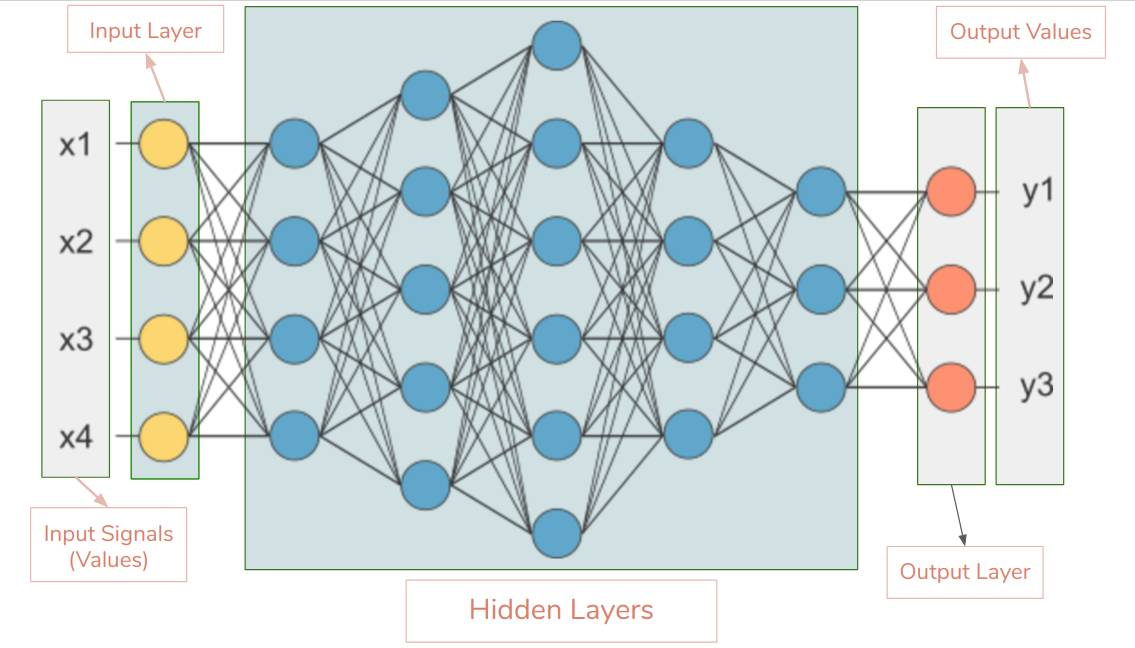
网上找了一张示意图,神经网络的基本结构包括:
- 输入层:接受原始数据,比如图像的像素、文本词语
- 隐藏层:一层或者多层。每一层存在很多“神经元”,在每个神经元可以做简单的加工(赋予权重求和,激活函数)
- 输出层:给出最终结果,比如分类标签、回归值
激活函数(Activation Function)
激活函数的作用,是让神经网络“能学会非线性的东西”。
如果只是简单的赋予权重然后再加和,即使有很多层隐藏层的加工,最终得到的结果仍然是线性的。因为无数次线性变化的叠加后,依然可以提炼为a*x + b的形式。但实际上有很多的结果属于非线性的,因此在线性化后需要引入非线性的操作,便于对非线性结果的拟合。这样每层加上非线性操作后,理论上只要层出足够多,那么对于任意复杂的非线性函数都能拟合。
而实现这一非线性操作的就是激活函数。常见的激活函数有:
| 名称 | 公式 / 行为 | 特点 |
|---|---|---|
| ReLU(最常用) | 负数变0,正数不变;计算快,效果好 | |
| Sigmoid | 把任意值压缩到 (0,1),像概率;但容易“梯度消失” | |
| Tanh | 压缩到 (-1,1),比 Sigmoid 对称,但也有梯度消失问题 |
损失函数(Loss Function)
就像传统的机器学习,训练的结果将使用评估指标来判断模型的效果。在神经网络训练中,评估指标就是损失函数(Loss Function)。损失函数得到的结果是:目标与训练结果的差距,也就是预测结果有多差。
比如在回归任务中常使用均方误差(MSE)来评估,而分类任务可能会使用交叉熵。
梯度下降(Gradient Descent)
很显然,为了训练的准确度,损失函数越小越好。与机器学习类似,神经网络也有调参的步骤,通过调整模型的权重和偏置,减小loss值,这个工具就是梯度下降。
根据数学知识,梯度就是:损失函数对每个参数的偏导数,进而得到loss变化的数值和方向。理论上讲,通过不断地调整,可以最终逼近或找到最低点(比如在二次函数中的最小值,切线为0)。换句话说,梯度下降就是用数学的方式“试错”,通过不断沿着损失函数最陡的下坡方向调整参数,最终找到让模型表现最好的那组权重。
那么,具体是怎么调整权重和偏置呢?使用的方法是反向传播法(Backpropagation),顾名思义,就是沿着与训练时相反的方向进行更新参数(前向传播,由输入到逐层计算到预测值),也就是
通过不断地迭代权重,计算梯度,最终逼近
时(
),就达到了收敛。
关于 (学习率)的取值:太大,每次下降的间距过大,可能会错过最低点,导致出现Loss越来越大的状况;太小,可以找到最低点,但是训练速度太慢,效率低下。
优化器(Optimizer)
由于基础梯度下降(SGD)存在以下缺陷:
- 学习率固定 → 太大震荡,太小太慢
- 所有参数用同一个学习率 → 不合理(有些参数该快调,有些该慢调)
- 容易卡在局部极小值或鞍点
- 收敛速度慢
因此,使用优化器,在梯度下降的基础上,改进参数更新的方式,解决基础方法的缺陷。
| 常见优化器 | 核心思想 |
|---|---|
| SGD(随机梯度下降) | 最基础:w←w−η⋅g |
| Momentum | 加入“惯性”,避免震荡,加速收敛;会参考之前走的方向 |
| Adam(最常用) | 自动调整每个参数的学习率,结合 Momentum 和 自适应学习率 |
简单MLP流程
依然选择使用鸢尾花数据(4特征,3分类)作为数据集。
首先加载数据,确定标签和特征,划分训练集和测试集:
# 导入数据
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
# 确定特征和标签
iris = load_iris()
X = iris.data
y = iris.target
# 划分训练集和测试集
X_train,X_test,y_train,y_test = train_test_split(X,y,train_size=0.8,random_state=42)
print(X_train.shape,X_test.shape,y_train.shape,y_test.shape)(1)数据预处理
归一化:由于神经网络对于输入数据的尺寸十分敏感,因此需要统一数据尺度。
# 归一化处理,统一数据尺度
from sklearn.preprocessing import MinMaxScaler
min_max_scaler = MinMaxScaler()
X_train = min_max_scaler.fit_transform(X_train)
X_test = min_max_scaler.transform(X_test) 张量转换:Pytorch是基于张量(Tensor)运算的深度学习框架,因此对于numpy数组等必须要转化为tensor类型。此外,在这里要注意转换的类型:
- 特征X:通常是连续值,在神经网络内部的激活函数、线性变换等都基于浮点运算,因此要讲输入特征转换为Float类型
- 分类标签y:通常是离散的整数类别,不需要参与浮点运算。在 CrossEntropyLoss 中要求标签是LongTensor(即int64)。但
BCEWithLogitsLoss(多标签分类常用)需 float。 - 回归值y:连续值,使用Float类型
# 张量转换,X_train等均为numpy数组
import torch
X_train = torch.FloatTensor(X_train)
X_test = torch.FloartTensor(X_test)
y_train = torch.LongTensor(y_train)
y_test = torch.LongTensor(y_test)(2)模型架构的定义
对于神经网络模型,最基本的结构包括三部分:一层输入层、一层隐藏层及一层输出层。
在代码实现上,首先继承nn.Module类(pytorch中所有神经网络模块的基类,必须继承),调用父类方法,这一步是固定模式。然后定义每一个层,输入和输出层使用的是全连接层(线性变换)nn.Linear(in_features_num, out_features_num) 。再定义前向传播流程forward:
fc1(x)→[batch_size, 10]relu(...)→ 保持形状[batch_size, 10],但负值变 0fc2(...)→[batch_size, 3],输出每个类别的“原始得分”(logits),原则上会有softmax计算概率,但是在损失函数中已包含,所以没有。
# 模型架构的定义
import torch
import torch.nn as nn
import torch.optim as optim
class MLP(nn.Module): # 定义一个多层感知机(MLP)模型,继承父类nn.Module
def __init__(self): # 初始化函数
super(MLP,self).__init__() # 调用父类的初始化函数
#定义层
self.fc1 = nn.Linear(4,10) # 将 4 维输入映射到 10 维隐藏表示
# 实际上上面这个代码也是在对线性层这个类进行初始化,只有先实例化了这个对象,后面才能调用它
self.relu = nn.ReLU() # 引入非线性,增强模型表达能力
self.fc2 = nn.Linear(10,3) # 将隐藏表示映射到 3 个类别的 logits
# 定义前向传播流程
def forward(self,x):
output = self.fc1(x)
output = self.relu(output)
output = self.fc2(output)
return output
# 实例化
model = MLP()
(3)定义损失函数和优化器
损失函数:由于是分类问题,选择交叉熵损失函数CrossEntropyLoss
优化器:SGD或Adam
# 定义损失函数和优化器
criterion = nn.CrossEntropyLoss()
# 优化器
optimiser = optim.SGD(model.parameters(),lr=0.01)
# optimiser = optim.Adam(model.parameters(),lr=0.001)(4)循环训练
epoch:模型完整遍历一遍训练数据的次数。由于神经网络通常不能一次就学会所有规律,所以需要多学几遍(即epoch的数值)。关于epoch数值的确定,先设置一个较大的值然后观察训练曲线,找到在欠拟合和过拟合之间的最佳epoch值。
确定训练的轮数(epoch值)后,按照前向传播训练→损失函数计算→反向传播计算梯度→更新参数优化,不断训练,直到达到收敛或训练轮数完成。
注意:由于Pytorch会累积梯度,所以在每次迭代计算梯度时,需要先清零再计算。
# 循环训练
epoch_num = 20000 # 训练的轮数
losses = [] # 存储每次循环的loss值,便于后续可视化
for i in range(epoch_num):
# 前向传播
output = model.forward(X_train) # 显式调用forward函数
# 损失函数计算
loss = criterion(output,y_train) # output是模型预测值,y_train是真实标签
# 反向传播
optimiser.zero_grad() # 清零
loss.backward() # 反向传播计算梯度
optimiser.step() # 更新参数
# 记录损失值
losses.append(loss.item())
#每100个,打印一次结果
if (epoch + 1) % 100 == 0:
print(f'Epoch [{epoch+1}/{num_epochs}], Loss: {loss.item():.4f}')
(5)可视化loss过程
将损失曲线进行可视化,绘制epoch-loss曲线,观察loss值下降情况。
# 可视化
import matplotlib.pyplot as plt
plt.plot(list(range(epoch_num)),losses)
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.title('Training Loss over Epochs')
plt.show()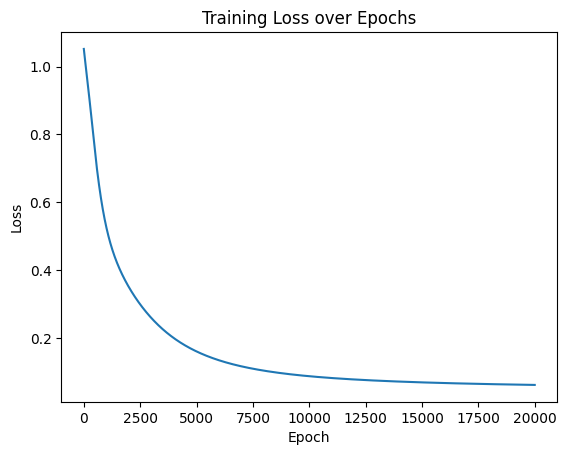





















 1030
1030

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








