从可观测性的角度研究基于扩展卡尔曼滤波器（EKF）的同时定位与地图构建（SLAM）中的不一致性问题（Matlab代码实现）

最新推荐文章于 2025-07-16 22:38:59 发布
原创 最新推荐文章于 2025-07-16 22:38:59 发布 · 565 阅读 · 15 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#matlab #算法 #开发语言

               💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

 ⛳️赠与读者

💥1 概述

1. 引言

2. EKF-SLAM基本原理与不一致性机制

3. 可观测性对EKF-SLAM一致性的影响

4. 解决EKF-SLAM不一致性问题的策略

5. 仿真验证与结果分析

6. 结论与展望

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码、文章

 ⛳️赠与读者

👨‍💻做科研，涉及到一个深在的思想系统，需要科研者逻辑缜密，踏实认真，但是不能只是努力，很多时候借力比努力更重要，然后还要有仰望星空的创新点和启发点。当哲学课上老师问你什么是科学，什么是电的时候，不要觉得这些问题搞笑。哲学是科学之母，哲学就是追究终极问题，寻找那些不言自明只有小孩子会问的但是你却回答不出来的问题。建议读者按目录次序逐一浏览，免得骤然跌入幽暗的迷宫找不到来时的路，它不足为你揭示全部问题的答案，但若能让人胸中升起一朵朵疑云，也未尝不会酿成晚霞斑斓的别一番景致，万一它居然给你带来了一场精神世界的苦雨，那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。

     或许，雨过云收，神驰的天地更清朗.......🔎🔎🔎

💥1 概述

从可观测性角度研究基于扩展卡尔曼滤波器（EKF）的同时定位与地图构建（SLAM）中的不一致性问题研究

摘要
本文从可观测性的角度研究了基于扩展卡尔曼滤波器（EKF）的同时定位与地图构建（SLAM）中的不一致性问题。我们通过分析证明，当过程和测量模型的雅可比矩阵在每个时间步骤中根据最新的状态估计值进行评估时，EKF中使用的线性化误差状态系统具有比实际非线性SLAM系统更高维度的可观测子空间。因此，EKF的协方差估计在状态空间中无信息可用的方向上会减小，这是不一致性的主要原因之一。基于这些理论结果，我们提出了一个改进EKF SLAM一致性的通用框架。在这个框架中，EKF的线性化点被选择以确保得到的线性化系统模型具有适当维度的可观测子空间。我们描述了两种算法，它们是这一范式的实例。第一种算法称为可观测性约束（OC）-EKF，其选择线性化点以最小化它们的预期误差（即线性化点与真实状态之间的差异），并满足可观测性约束。第二种算法中，滤波器的雅可比矩阵使用所有状态变量的第一次可用估计进行计算。这种方法称为第一估计雅可比矩阵（FEJ）-EKF。提出的算法经过了仿真和实验测试，显示出在准确性和一致性方面明显优于标准EKF。

关键词：同时定位与地图构建，非线性估计，扩展卡尔曼滤波器，线性化误差，估计器不一致性，可观测性

扩展卡尔曼滤波器（EKF）作为SLAM领域的经典算法，因计算效率高被广泛应用。然而，EKF-SLAM在处理非线性系统时存在固有的不一致性问题，表现为估计协方差矩阵系统性低估真实误差，导致滤波器对自身估计过于自信。这种不一致性会降低定位精度和地图质量，甚至引发系统发散。本文从可观测性理论出发，深入剖析EKF-SLAM不一致性的根本原因，提出改进策略，并通过仿真验证改进算法的有效性。

1. 引言

SLAM技术是移动机器人自主导航的核心，其目标是在未知环境中实时构建地图并确定自身位姿。EKF凭借其相对简单的计算过程和较低的计算复杂度，成为早期SLAM系统中的主流算法。然而，EKF-SLAM算法基于线性化假设，当系统具有显著的非线性特性时，线性化误差会逐渐累积，导致机器人姿态估计和地图构建结果出现偏差，甚至发散，最终引发严重的不一致性问题。

2. EKF-SLAM基本原理与不一致性机制

2.1 EKF-SLAM概述
EKF-SLAM将机器人位姿和环境中观测到的特征点状态作为状态向量的一部分进行估计。系统模型包括运动模型和观测模型：

  • 运动模型：描述机器人位姿随时间的变化规律，通常采用匀速或匀加速运动模型。
  • 观测模型：描述传感器观测值与机器人位姿及地图特征之间的关系，例如激光雷达的测距和测角模型。

2.2 不一致性产生机制
EKF-SLAM的不一致性主要源于以下因素：

  • 线性化误差：EKF通过一阶泰勒展开将非线性系统近似为线性系统，这种近似在系统高度非线性或估计误差较大时引入显著误差，导致协方差矩阵低估真实误差。
  • 数据关联错误：错误的观测数据与地图特征点匹配会导致状态估计和协方差错误更新，加剧不一致性。
  • 特征初始化不准确：新观测到的特征点初始化误差会扩散到整个状态向量，影响后续估计。
3. 可观测性对EKF-SLAM一致性的影响

3.1 可观测性理论
可观测性描述了从系统输出中推断系统内部状态的能力。对于EKF-SLAM而言，良好的可观测性是确保一致性估计的前提。

3.2 机器人轨迹的可观测性

  • 直线运动或纯旋转运动：若缺少足够的特征点观测，机器人位姿可能存在退化，导致轨迹可观测性不足。
  • 特征点分布：特征点分布稀疏或对称时，机器人位姿估计的唯一性受到影响，降低可观测性。

3.3 地图特征的可观测性

  • 观测视角：特征点仅被短暂观测或观测视角变化不大时，其位置估计精度较低，影响地图一致性。
  • 多视角观测：通过多视角观测提高特征点位置的可观测性，可减少初始化误差。
4. 解决EKF-SLAM不一致性问题的策略

4.1 改进线性化方法

  • 高阶泰勒展开：采用更高阶的泰勒展开减少线性化误差，但计算复杂度增加。
  • 无迹卡尔曼滤波（UKF）：使用确定性采样点（sigma points）近似非线性函数的均值和协方差，避免雅可比矩阵计算，减少线性化误差。
  • 容积卡尔曼滤波（CKF）：采用球面-径向容积规则选择采样点，在某些情况下性能优于UKF。

4.2 改进数据关联方法

  • 多假设跟踪（MHT）：考虑多个数据关联假设，使用概率评估可能性，通过延迟决策减少错误关联风险。
  • 动态调整门限：根据不确定性动态调整数据关联门限，降低错误关联概率。
  • 鲁棒特征描述子：使用更具辨识度的特征描述子，降低相似特征点混淆风险。

4.3 基于子地图的SLAM

  • 子地图划分：将地图划分为多个子地图，分别进行SLAM，再进行全局融合，减少计算量并提高精度。
  • 局部一致性保障：在子地图内部保障一致性，减少全局不一致性传播。

4.4 可观测性约束方法

  • 可观测性约束EKF（OC-EKF）：选择线性化点以满足可观测性约束，减少协方差低估。
  • 第一估计雅可比矩阵EKF（FEJ-EKF）：使用所有状态变量的第一次可用估计计算雅可比矩阵，避免协方差矩阵膨胀。
5. 仿真验证与结果分析

5.1 仿真环境设置

  • 机器人模型：采用两轮差速驱动机器人模型，运动模型为匀速模型。
  • 传感器模型：激光雷达模型，包含测距和测角噪声。
  • 环境设置：包含多个特征点的二维平面环境，特征点分布均匀。

5.2 算法实现

  • 标准EKF：实现标准EKF-SLAM算法，作为基准对比。
  • FEJ-EKF：实现第一估计雅可比矩阵EKF，改进线性化点选择。
  • UKF-SLAM：实现无迹卡尔曼滤波SLAM，避免线性化误差。

5.3 仿真结果

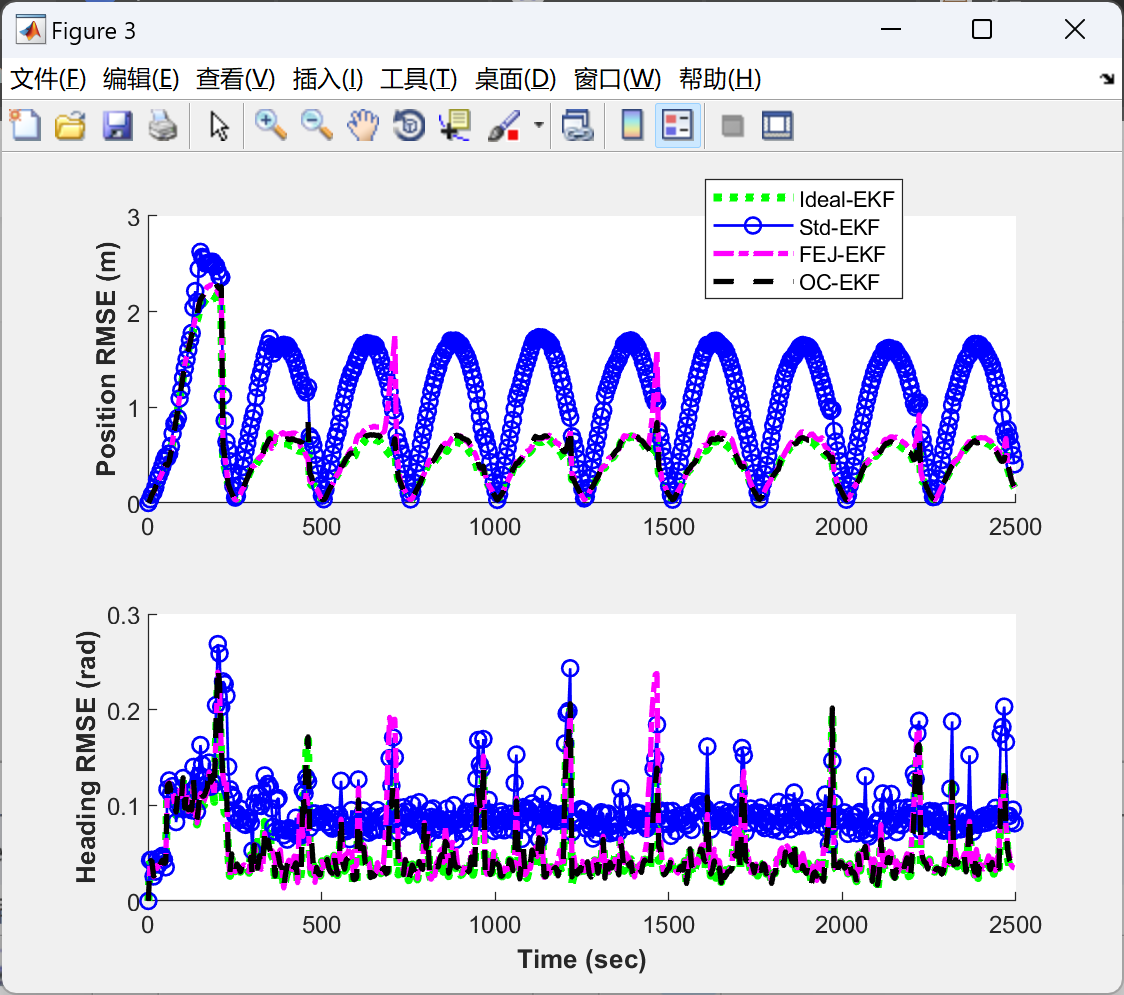
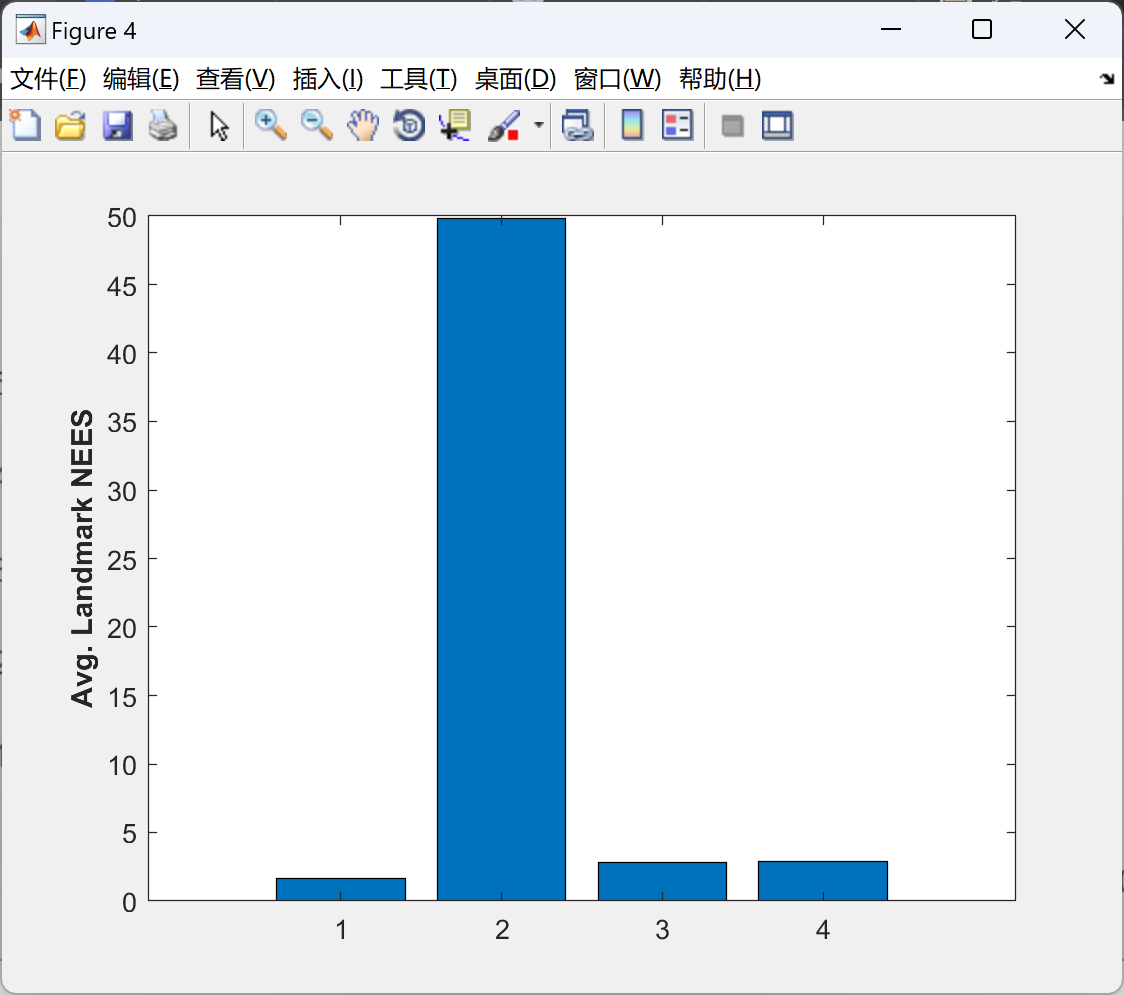
  • 定位精度：FEJ-EKF和UKF-SLAM的定位精度显著高于标准EKF，尤其在长时间运行后。
  • 地图一致性：FEJ-EKF和UKF-SLAM构建的地图特征点位置误差更小，地图一致性更高。
  • 协方差估计：标准EKF的协方差矩阵系统性低估真实误差，而FEJ-EKF和UKF-SLAM的协方差估计更接近真实值。
6. 结论与展望

6.1 研究结论
本文从可观测性角度深入分析了EKF-SLAM中的不一致性问题，提出FEJ-EKF和UKF-SLAM等改进方法。仿真结果表明，改进算法显著提高了定位精度和地图一致性，验证了可观测性约束和改进线性化方法的有效性。

6.2 未来展望

  • 多传感器融合：结合视觉、激光、IMU等多种传感器信息，提高SLAM系统的鲁棒性和精度。
  • 深度学习应用：利用深度学习技术提高地图匹配和数据关联精度，解决不一致性问题。
  • 分布式SLAM：针对大型环境，研究分布式SLAM算法，提高效率和鲁棒性。

📚2 运行结果

部分代码：

sigma_v = sigma/sqrt(2); %.1*v_true; %
sigma_w = 2*sqrt(2)*sigma; %.1*omega_true; 1*pi/180; %
Q = diag([sigma_v^2 sigma_w^2]);

sigma_p = .1; %noise is the percentagae of distance measurement, BUT double check rws.m since sometimes we use this as a constant absolute sigma
sigma_r = 1; %range measmnt noise
sigma_th = 10*pi/180;%bearing measuremnt noise

nL = 20; %number of landmarks
nSteps = 2500; %nubmer of time steps
nRuns = 5; %number of monte carlo runs
if nL==1
    max_range = 200;%always observe this landmark
else
    max_range = 5;%env_size/10;%.5*v_true/omega_true;%
end
min_range = .5;
init_steps = 0;%3
max_delay = 10;%for delayed initial
NIncr = 0; %increment number of incremental MAP: 0 - not runing


%% preallocate memory for saving resutls

% Ideal EKF
xRest_id = zeros(3,nSteps,nRuns); %estimated traj
xRerr_id = zeros(3,nSteps,nRuns); %all err state
Prr_id = zeros(3,nSteps,nRuns); %actually diag of Prr
neesR_id = zeros(1,nSteps,nRuns); %nees (or mahalanobis distance)
rmsRp_id =  zeros(1,nSteps,nRuns); %rms of robot position
rmsRth_id = zeros(1,nSteps,nRuns); %rms of robot orientation
xLest_id = zeros(2,nL,nSteps,nRuns);
xLerr_id = zeros(2,nL,nSteps,nRuns);
Pll_id = zeros(2,nL,nSteps,nRuns);
neesL_id = zeros(1,nL,nSteps,nRuns);
rmsL_id = zeros(1,nL,nSteps,nRuns);
nees_id = zeros(1,nSteps,nRuns); %nees for the whole state

% Standard EKF
xRest_std = zeros(3,nSteps,nRuns); %estimated traj
xRerr_std = zeros(3,nSteps,nRuns); %all err state
Prr_std = zeros(3,nSteps,nRuns); %actually diag of Prr
neesR_std = zeros(1,nSteps,nRuns); %nees (or mahalanobis distance)
rmsRp_std =  zeros(1,nSteps,nRuns); %rms of robot position
rmsRth_std = zeros(1,nSteps,nRuns); %rms of robot orientation
xLest_std = zeros(2,nL,nSteps,nRuns);
xLerr_std = zeros(2,nL,nSteps,nRuns);
Pll_std = zeros(2,nL,nSteps,nRuns);
neesL_std = zeros(1,nL,nSteps,nRuns);
rmsL_std = zeros(1,nL,nSteps,nRuns);
nees_std = zeros(1,nSteps,nRuns); %nees for the whole state
kld_std = zeros(1,nSteps,nRuns); % KLD

% FEJ-EKF
xRest_fej = zeros(3,nSteps,nRuns); %estimated traj
xRerr_fej = zeros(3,nSteps,nRuns); %all err state
Prr_fej = zeros(3,nSteps,nRuns); %actually diag of Prr
neesR_fej = zeros(1,nSteps,nRuns); %nees (or mahalanobis distance)
rmsRp_fej =  zeros(1,nSteps,nRuns); %rms of robot position
rmsRth_fej = zeros(1,nSteps,nRuns); %rms of robot orientation
xLest_fej = zeros(2,nL,nSteps,nRuns);
xLerr_fej = zeros(2,nL,nSteps,nRuns);
Pll_fej = zeros(2,nL,nSteps,nRuns);
neesL_fej = zeros(1,nL,nSteps,nRuns);
rmsL_fej = zeros(1,nL,nSteps,nRuns);
nees_fej = zeros(1,nSteps,nRuns); %nees for the whole state
kld_fej = zeros(1,nSteps,nRuns); % KLD

% OC-EKF
xRest_ocekf_1 = zeros(3,nSteps,nRuns); %estimated traj
xRerr_ocekf_1 = zeros(3,nSteps,nRuns); %all err state
Prr_ocekf_1 = zeros(3,nSteps,nRuns); %actually diag of Prr
neesR_ocekf_1 = zeros(1,nSteps,nRuns); %nees (or mahalanobis distance)
rmsRp_ocekf_1 =  zeros(1,nSteps,nRuns); %rms of robot position
rmsRth_ocekf_1 = zeros(1,nSteps,nRuns); %rms of robot orientation
xLest_ocekf_1 = zeros(2,nL,nSteps,nRuns);
xLerr_ocekf_1 = zeros(2,nL,nSteps,nRuns);
Pll_ocekf_1 = zeros(2,nL,nSteps,nRuns);
neesL_ocekf_1 = zeros(1,nL,nSteps,nRuns);
rmsL_ocekf_1 = zeros(1,nL,nSteps,nRuns);
nees_ocekf_1 = zeros(1,nSteps,nRuns); %nees for the whole state
kld_ocekf_1 = zeros(1,nSteps,nRuns); % KLD


%% LANDMARK GENERATION: same landmarks in each run
if nL==1
    xL_true_fixed = [0;v_true/omega_true];
elseif nL==2
    xL_true_fixed = [5 -5; 5 15];
else
    xL_true_fixed = gen_map(nL,v_true,omega_true,min_range, max_range, nSteps,dt);%max_range=5
end


%% Monte Carlo Simulations

tic
for kk = 1:nRuns
    
    kk
    
    % % real world simulation data % %
    xL_true(:,:,kk) = xL_true_fixed;
    [v_m,omega_m, v_true_all,omega_true_all, xR_true(:,:,kk), z,R] = rws(nSteps, dt,v_true,omega_true,sigma_v,sigma_w,sigma_r,sigma_th,sigma_p,xL_true(:,:,kk),max_range,min_range);
    
    
    % % INITIALIZATION
    x0 = zeros(3,1);
    if init_steps
        P0 = zeros(3);
    else
        P0 = diag([(.0001)^2,(.0001)^2,(.0001)^2]);
    end
    
    for k=1:init_steps
        [x0,P0] = propagate_std(x0,P0,dt,v_m(k),omega_m(k),sigma_v,sigma_w);
    end
    
    
    % Ideal EKF
    xe_id = x0;
    Pe_id = P0;
    V_id = [];
    
    % Standard EKF
    xe_std = x0;
    Pe_std = P0;
    V_std = [];
    
    
    % FEJ-EKF
    xe_fej = x0;
    Pe_fej = P0;
    xL_fej_1 = [];
    xR_fej_k_k1 = xe_fej(1:3,1);
    PHI_mult_fej = eye(1); %propagation jacobian product
    V_fej = [];
    
    % OC-EKF
    xe_ocekf_1 = x0;
    Pe_ocekf_1 = P0;
    xL_ocekf_1_1 = [];
    xR_oc_k_k1_1 = xe_ocekf_1(1:3,1);
    dpR_star_prev_1 = zeros(2,1);
    pR_star_prev = x0(1:2,1);
    dpR_ocekf_1 = zeros(2,1);
    V_ocekf_1 = [];
    PHI_mult_ocekf_1 = eye(1);
    lambda_1 = zeros(2,nL);
    
    
    
    % list of landmark ids that sequentially appear in the state vector
    lm_seq_id = [];
    lm_seq_std = [];
    lm_seq_fej = [];
    lm_seq_ocekf_1 = [];
 

🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。

🌈4 Matlab代码、文章

资料获取，更多粉丝福利，MATLAB|Simulink|Python资源获取

                                                           在这里插入图片描述

从可观测性的角度研究基于扩展卡尔曼滤波器（EKF）的同时定位与地图构建（SLAM）中的不一致性问题附Matlab代码
Matlab_jiqi的博客
05-29 680
同时定位与地图构建（SLAM）是移动机器人领域的核心问题，旨在使机器人在未知环境中构建地图的同时，估计自身的位置和姿态。扩展卡尔曼滤波器（EKF）因其高效性，长期以来是解决SLAM问题的主流方法之一。然而，基于EKF的SLAM算法普遍存在估计不一致性问题，即估计协方差矩阵对真实误差的低估，从而导致对估计结果置信度的错误评估。本文将从可观测性理论的角度深入剖析EKF-SLAM中的不一致性问题。首先，我们将回顾EKF-SLAM的基本原理，并阐述不一致性的产生机制。
【滤波跟踪】基于扩展卡尔曼滤波器EKF的同时定位与地图构建SLAM中的不一致性问题附Matlab代码实现
m0_60703264的博客
12-08 699
摘要: 同步定位与地图构建 (SLAM) 技术旨在机器人自主导航中实现实时定位和环境地图构建。扩展卡尔曼滤波器 (EKF) 作为一种经典的SLAM算法，因其计算效率高而被广泛应用。然而，EKF-SLAM 算法在处理非线性系统时存在固有的线性化误差，这会导致地图和机器人姿态的不一致性问题，从而影响定位精度和地图质量。本文将深入探讨 EKF-SLAM 中的不一致性问题，分析其成因，并综述一些常用的解决方法，最终展望该领域未来的发展方向。
从可观测性的角度研究基于扩展卡尔曼滤波器（EKF）的同时定位与地图构建（SLAM）中的不一致性问题附Matlab代码.rar
05-24
本文件提供了一套基于Matlab平台的解决方案，旨在从可观测性的角度来研究SLAM中应用EKF时出现的不一致性问题。Matlab作为一种高级数值计算和可视化软件，具有强大的矩阵运算和数据处理能力，非常适合进行SLAM问题的...
安装MATLAB流程中遇到的问题
娃哈哈喽Zzz
07-15 190
在安装完成后，需要激活之前，点击图标没有任何显示。原因是之前安装了2017b版本，在启动时会与之前的残余文件有冲突。所以在win搜索栏中输入“%AppData%”，会出现“C:\Users\angel\AppData\Roaming”，删除原来已有的MATLAB文件。重启新安装的MATLAB文件。
评估遥感云雾浓度的无参化指标（适用于其它合成雾的场景）
m0_62919535的博客
07-16 416
本文总结了四种用于评估遥感图像云雾浓度的无参考指标：FADE、densityD、AuthESI和JSFD。FADE通过MATLAB实现，能较好反映雾气浓度但计算耗时；densityD基于TensorFlow，对天空场景较为敏感；AuthESI主要用于评估合成雾真实性，不适用于浓度评估；JSFD结合HSV空间S值、白点比例和暗通道特征，准确性较高但计算时间长。实验表明，FADE和JSFD更适合遥感场景的雾浓度评估，虽然存在计算效率问题，但能较好区分薄雾和浓雾数据集。这些指标为遥感图像去雾研究提供了有效的量化评
【MATLAB代码】基于Taylor迭代的二维TOA定位解算程序，锚点数量可自由设置。附完整的源代码，订阅专栏后可以查看
MATLAB卡尔曼的博客
07-16 17
摘要：本文研究了基于Taylor迭代的二维TOA定位算法，适用于非高斯噪声环境。通过仿真实验验证了该方法在4个和40个锚点下的有效性，展示了定位结果与误差收敛曲线。文中详细推导了迭代线性化过程，并提供完整的MATLAB代码实现，包括参数设置、TOA建模、迭代解算及可视化分析。结果表明，Taylor方法在合理初值下能快速收敛到高精度解，为UWB等测距定位系统提供了实用算法参考。代码可直接运行复现结果。
基于Matlab改进大津法和Gabor滤波的织物缺陷检测系统
ZSW1218的博客
07-16 344
随着自动化技术的发展，织物缺陷检测已经成为纺织工业中的一个重要课题。传统的人工检测不仅效率低，而且容易受到主观因素的影响，因此，基于计算机视觉的自动检测方法得到了广泛的研究。本文提出了一种基于MATLAB的织物缺陷检测系统，该系统结合了改进的大津法（Otsu’s method）和Gabor滤波器（Gabor Filter）来实现高效、准确的缺陷检测。首先，利用Gabor滤波器提取织物图像中的纹理特征，通过多方向和多尺度的滤波器对不同纹理进行敏感性增强，从而提升织物表面细节的识别能力。然后，采用改进的大津法对
【代码】Matlab鸟瞰图函数
RickyWasYoung的博客
07-16 48
用matlab把图像转化为鸟瞰图。
一维时间序列的贝塔分布拟合算法matlab仿真
熟悉python,matlab,C,C++,JAVA等
07-15 911
本文介绍了贝塔分布在一维时间序列拟合中的应用。贝塔分布是一种定义在(0,1)区间内的双参数连续概率分布，通过形状参数α和β可以灵活刻画数据的分布特征。文章阐述了贝塔分布在比例型时间序列建模中的优势，包括股票涨跌幅、设备故障率等场景。内容涵盖程序功能描述、测试软件版本、部分程序代码、算法理论概述以及参考文献。理论部分重点讲解了贝塔分布的概率密度函数、数据预处理要求和平稳性检验方法，为比例型时间序列分析提供了可靠的概率模型解决方案。
Matlab数字图像处理——基于形态学的水果识别系统（可识别多种水果）
小嘤熊的博客
07-16 103
形态学操作用一些固定形状的“探测器”来清理图像中的噪声；轮廓提取在清晰的轮廓上填补内部空洞，并只保留边缘的像素。Matlab数字图像处理——基于形态学的水果识别系统（可识别多种水果）小编会不定期发布相关设计内容包括但不限于如下内容:信号处理、通信仿真、算法设计、matlab appdesigner，gui设计、simulink仿真......希望能帮到你！
145-变分模态分解VMD与平稳小波变换SWT信号降噪算法实现！
m0_53992455的博客
07-15 756
简介：VMD-SWTTV是一种针对一维信号的二级框架降噪算法，结合了变分模态分解VMD与平稳小波变换SWT，并采用了小波变换全变分法优化了SWT。降噪效果还是不错的。VMD-SWTTV是一种针对一维信号的二级框架降噪算法，结合了变分模态分解VMD与平稳小波变换SWT，并采用了小波变换全变分法优化了SWT。使用仿真数据与最近的一些算法VMD-WTD、SVD-VMD、JANRR、EEMD-SP进行了降噪效果的对比，一定的信噪比范围，首先使用VMD对信号进行自适应分解，在确定分解层级与主要IMF分量的选择时，
多目标优化|HKELM混合核极限学习机+NSGAII算法工艺参数优化、工程设计优化，四目标（最大化输出y1、最小化输出y2,y3,y4），Matlab完整源码
最新发布
机器学习之心的博客，关注并私信文章链接，获取对应文章源码和数据。
07-16 714
多目标优化|HKELM混合核极限学习机+NSGAII算法工艺参数优化、工程设计优化，四目标（最大化输出y1、最小化输出y2,y3,y4），Matlab完整源码
基于MATLAB的决策树DT的数据分类预测方法应用
张陈亚的博客
07-16 670
摘要：本项目基于MATLAB平台实现决策树分类预测模型，使用2000条完整数据（11个特征变量）进行训练。通过数据预处理、特征工程（80%训练集/20%验证集划分及标准化）和模型构建，最终模型在测试集上表现优异：准确率96.75%、F1值96.77%，混淆矩阵显示误判样本仅13个。项目完整包含数据、代码及文档，证实了决策树算法在实际分类任务中的有效性，可作为产品建模的可靠工具。（149字）
M00218-柑橘感染青霉病过程元胞自动机模拟matlab
crasher123的博客
07-13 107
的过程，并且使用MATLAB进行实现。通过这种模拟方法，我们不仅能够更直观地观察病害传播的过程，还能为农业病害的防控提供理论依据。在农业研究中，模拟植物病害的传播过程一直是一个重要的研究方向，尤其是在控制和预防植物病害方面。今天，将为大家介绍一种基于。M00218-柑橘感染青霉病过程元胞自动机模拟matlab。
基于MATLAB的BP神经网络的时间序列数据预测方法应用
张陈亚的博客
07-14 987
本文介绍了一个基于MATLAB的BP神经网络时间序列预测项目。针对工业、金融等领域时间序列的非线性特点，项目构建了包含10个隐藏层节点的BP神经网络模型。通过数据预处理、特征工程和模型训练，实现了R方0.9785的高精度预测效果。实验结果表明，该模型能有效捕捉时间序列特征，预测值与真实值拟合良好。项目提供了完整的数据、代码和文档，适用于工程监测、经济分析等场景，为时间序列预测提供了可靠的技术方案。
电阻抗成像肺功能测试数据分析与直方图生成
huanghm88的专栏
07-13 37
本文介绍了基于MATLAB的电阻抗成像(EIT)肺功能测试数据分析方法。研究针对32×32像素的EIT图像序列，通过三步算法处理：首先计算特定时间点与谷值图像的差值，然后分析1秒后峰值与1秒值的差值，最终计算比值矩阵并处理异常值。系统展示了数据预处理、关键时间点检测、比值计算及统计分析的全流程，包括生成概率分布直方图和空间分布图等可视化方法。该分析为无创肺功能评估提供量化指标，可应用于临床呼吸监测和疾病诊断。
【数据同化案例1】ETKF求解 Lorenz-63 模型的同化系统（完整MATLAB实现）
WW、forever的博客
07-15 1005
ETKF求解 Lorenz-63 模型的同化系统
EKF扩展卡尔曼滤波器与图优化技术
04-03
<think>好的，我现在需要帮助用户理解扩展卡尔曼滤波器（EKF）与图优化技术的关系以及它们的应用场景和比较。首先，我得回顾一下这两种技术的基本概念，然后找出它们的联系和区别。 用户提到EKF和图优化，可能是在状态估计或SLAM（同时定位与地图构建）领域遇到相关问题。EKF是处理非线性系统状态估计的传统方法，而图优化则是更现代的优化技术，比如在SLAM中使用因子图。我需要比较两者的原理、实现复杂度、计算效率、应用场景等。 首先，EKF的工作原理。EKF通过线性化非线性模型来处理状态估计，使用泰勒展开对系统模型和观测模型进行一阶近似。这种方法在轻度非线性情况下效果不错，但强非线性或长时间运行时误差可能累积，导致估计不准确。参考中提到的EKF在雷达跟踪的例子，说明它在实时系统中应用较多，计算量相对较低，但需要频繁的雅可比矩阵计算。 然后是图优化技术。图优化将状态估计问题建模为图结构，节点代表状态变量，边代表观测或约束。通过最小化所有约束的误差来优化状态估计。这种方法通常使用批量优化，比如高斯-牛顿法或列文伯格-马夸尔特算法，能处理非线性问题而不需要线性化，因此在强非线性或大范围环境下更优。例如，在SLAM中，图优化可以更好地处理回环检测，优化整个轨迹和地图。 接下来比较两者的优缺点。EKF的计算复杂度较低，适合实时系统，但线性化误差可能影响精度，尤其是在高度非线性或长期运行的情况下。图优化虽然精度高，能处理全局优化，但计算量大，尤其是随着节点增加，优化时间增长，可能不适合实时性要求高的场景。 应用场景方面，EKF适用于需要快速估计且非线性程度不高的系统，比如机器人定位、传感器融合。图优化则适用于需要高精度和全局一致性的应用，如SLAM、三维重建、离线数据处理等。 实现复杂度上，EKF需要推导雅可比矩阵，对模型要求高，而图优化依赖于优化库，如g2o或Ceres，实现更灵活，但需要处理稀疏矩阵和大规模优化问题。 用户可能还想知道在SLAM中两者如何选择。比如，EKF SLAM早期使用较多，但随着环境复杂化，图优化逐渐成为主流，因为它能更好地处理回环和全局优化。需要引用相关文献或示例，如引用中的雷达跟踪例子，可能可以对比EKF和UKF，但用户的问题是关于图优化的，所以需要调整重点。 最后，总结两者的关系：都是状态估计方法，但EKF基于递归贝叶斯滤波，图优化基于批量优化。EKF适合实时、低计算场景，图优化适合高精度、复杂场景。在SLAM中，图优化逐渐取代EKF成为主流方法。</think>### EKF扩展卡尔曼滤波器与图优化技术比较及应用 #### 一、核心概念对比 1. **EKF扩展卡尔曼滤波器** - 基于**递归贝叶斯估计**，通过局部线性化（泰勒展开）处理非线性系统模型[^4] - 状态更新公式： $$ \hat{x}_{k|k} = \hat{x}_{k|k-1} + K_k (z_k - h(\hat{x}_{k|k-1})) $$ 其中雅可比矩阵$J_h$需实时计算[^1] - 特点：实时性强，但累积线性化误差可能影响长期精度 2. **图优化技术** - 将状态估计建模为**因子图**（Factor Graph），通过最小化全局误差函数优化状态变量[^2] - 目标函数示例： $$ X^* = \arg\min_X \sum_{i} \| f_i(x_i) - z_i \|_{\Sigma_i}^2 $$ - 特点：支持批量优化，可处理复杂约束（如SLAM中的回环闭合） #### 二、技术特性比较 | 特性 | EKF | 图优化 | |---------------------|------------------------------|---------------------------| | **实现原理** | 递归滤波+局部线性化 | 全局优化+非线性最小二乘 | | **计算复杂度** | $O(n^2)$（n为状态维度） | $O(m^3)$（m为节点数量） | | **精度影响** | 线性化误差累积 | 全局最优性保证 | | **实时性** | 适合在线处理 | 更适合离线/延迟优化 | | **约束处理能力** | 仅支持时序约束 | 支持任意拓扑约束 | #### 三、典型应用场景 1. **EKF适用场景** - 实时导航系统（如无人机姿态估计）[^3] - 传感器融合（IMU+GPS数据融合） - 短期目标跟踪（雷达/声呐跟踪） 2. **图优化适用场景** - SLAM（如Google Cartographer建图系统） - 三维重建（Bundle Adjustment优化） - 长时间轨迹优化（自动驾驶路径规划） #### 四、算法实现差异 **EKF实现关键步骤** ```python # 以雷达跟踪为例[^3] def ekf_predict(x, P, F, Q): x = F @ x P = F @ P @ F.T + Q return x, P def ekf_update(x, P, z, H, R): K = P @ H.T @ np.linalg.inv(H @ P @ H.T + R) x = x + K @ (z - H @ x) P = (np.eye(len(x)) - K @ H) @ P return x, P ``` **图优化实现框架（以g2o为例）** ```cpp // SLAM中的位姿图优化 g2o::SparseOptimizer optimizer; g2o::BlockSolverX::LinearSolverType* linearSolver = new g2o::LinearSolverCholmod<g2o::BlockSolverX::PoseMatrixType>(); g2o::BlockSolverX* solver_ptr = new g2o::BlockSolverX(linearSolver); optimizer.setAlgorithm(new g2o::OptimizationAlgorithmLevenberg(solver_ptr)); // 添加顶点（机器人位姿） g2o::VertexSE2* v = new g2o::VertexSE2(); v->setId(0); optimizer.addVertex(v); // 添加边（里程计约束） g2o::EdgeSE2* e = new g2o::EdgeSE2(); e->setVertex(0, optimizer.vertex(0)); e->setMeasurement(odometry); optimizer.addEdge(e); optimizer.initializeOptimization(); optimizer.optimize(10); ``` #### 五、技术融合趋势 现代SLAM系统（如LIO-SAM）常采用**混合架构**： - 前端使用EKF/UKF进行实时状态预测 - 后端采用图优化进行全局一致性调整 - 典型数据流： ``` 传感器数据 → EKF局部滤波 → 因子图构建 → 周期性地全局优化 → 反馈校正 ```
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值