本文详细介绍了定积分在近似计算、微元法及几何和物理问题中的应用。讨论了矩形法、梯形法和辛普森积分法的误差，并展示了如何利用这些方法计算面积、体积、弧长和做功。同时，提到了压力、引力等物理问题的积分解法。
高等数学笔记-乐经良
第五章-积分(Ⅱ)-定积分的应用
第六节 定积分的应用
一、近似计算
01 矩形法
-
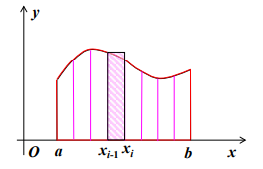
从几何意义上考虑，将曲边梯形分成 nnn 个小曲边梯形（底边等长）
-
用矩形近似小曲边梯形，则其面积近似：
f(xi−1)Δxi=f(xi−1)(b−a)n=yi−1(b−a)n f\left(x_{i-1}\right) \Delta x_{i}=f\left(x_{i-1}\right) \frac{(b-a)}{n}=y_{i-1} \frac{(b-a)}{n} f(xi−1)Δxi=f(xi−1)n(b−a)=yi−1n(b−a) -
导出近似公式：
∫abf(x)dx=∑i=1nb−anf(xi−1)=b−an(y0+y1+⋯+yn−1) \int_{a}^{b} f(x) d x=\sum_{i=1}^{n} \frac{b-a}{n} f\left(x_{i-1}\right)=\frac{b-a}{n}\left(y_{0}+y_{1}+\cdots+y_{n-1}\right) ∫abf(x)dx=i=1∑nnb−af(xi−1)=nb−a(y0+y1+⋯+yn−1) -
也可取右端边长为矩形高，得右矩形公式
-
误差为1/n1/n1/n 的同阶无穷小
02 梯形法
-
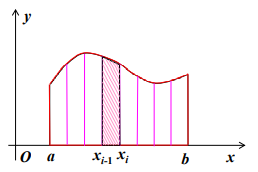
从几何意义上考虑，将曲边梯形分成 nnn 个小曲边梯形（底边等长）
-
用梯形近似小曲边梯形，则其面积近似：
f(xi−1)+f(xi)2Δxi=(b−a)(yi−1+yi)2n \frac{f\left(x_{i-1}\right)+f\left(x_{i}\right)}{2} \Delta x_{i}=\frac{(b-a)\left(y_{i-1}+y_{i}\right)}{2 n} 2f(xi−1)+f(xi)Δxi=2n(b−a)(yi−1+yi) -
导出近似公式：
∫abf(x)dx=b−a2n[(y0+yn)+2(y1+⋯+yn−1)] \int_{a}^{b} f(x) d x=\frac{b-a}{2 n}\left[\left(y_{0}+y_{n}\right)+2\left(y_{1}+\cdots+y_{n-1}\right)\right] ∫abf(x)dx=2nb−a[(y0+yn)+2(
最低0.47元/天 解锁文章
扫一扫
1487
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
