繁星数学随想录·笔记卷
函数性质卷
关于间断点的一些思考
一、初等函数与绝对值函数
01 f(∣x∣)f(|x|)f(∣x∣) 型

02 f(1x)f(\frac{1}{x})f(x1) 型

03 f(1∣x∣)f(\frac{1}{|x|})f(∣x∣1) 型

04 f(∣x∣)⋅g(x)f(|x|) \cdot g(x)f(∣x∣)⋅g(x) 型
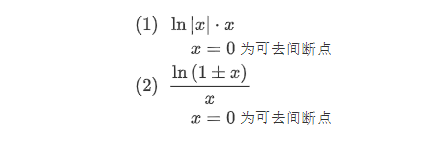
05 f(∣x∣)⋅g(1x)f(|x|) \cdot g(\frac{1}{x})f(∣x∣)⋅g(x1) 型
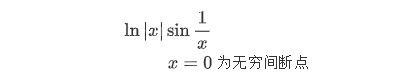
06 f(1∣x∣)⋅g(1x)f(\frac{1}{|x|}) \cdot g(\frac{1}{x})f(∣x∣1)⋅g(x1) 型
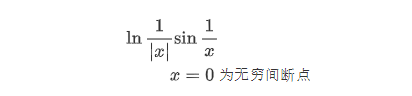
07 limn→∞f(x)\lim \limits_{n \rightarrow \infty} f(x)n→∞limf(x) 型

二、一个例子
判断下列函数在 x=0x=0x=0 处是何种间断点:
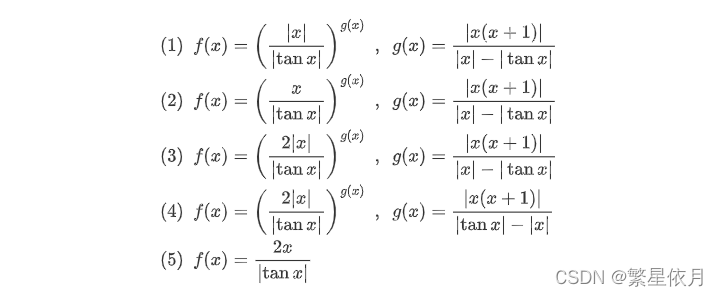
(1) x=0x=0x=0 为可去间断点
(2) x=0x=0x=0 为震荡间断点
(3) x=0x=0x=0 为可去间断点
(4) x=0x=0x=0 为无穷间断点
(5) x=0x=0x=0 为跳跃间断点




 本文探讨了初等函数与绝对值函数结合形成的七种函数类型在x=0处可能的间断点性质,包括可去、震荡、无穷和跳跃间断点。通过具体例子分析了函数在该点的行为,帮助理解函数连续性和间断性的概念。
本文探讨了初等函数与绝对值函数结合形成的七种函数类型在x=0处可能的间断点性质,包括可去、震荡、无穷和跳跃间断点。通过具体例子分析了函数在该点的行为,帮助理解函数连续性和间断性的概念。
















 577
577

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








