洛谷P4009：汽车加油行驶问题

题目描述

      给定一个N×N 的方形网格，设其左上角为起点◎，坐标(1,1) ，X 轴向右为正， Y 轴向下为正，每个方格边长为 1，如图所示。

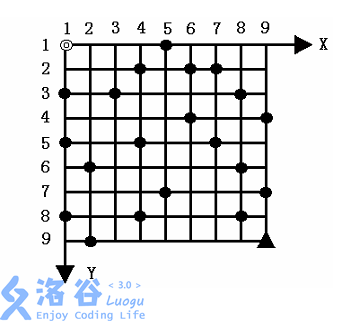
      一辆汽车从起点◎出发驶向右下角终点▲，其坐标为(N,N) 。

      在若干个网格交叉点处，设置了油库，可供汽车在行驶途中加油。汽车在行驶过程中应遵守如下规则:

1. 汽车只能沿网格边行驶，装满油后能行驶 K 条网格边。出发时汽车已装满油，在起点与终点处不设油库。

2. 汽车经过一条网格边时，若其 X 坐标或 Y 坐标减小，则应付费用 B ，否则免付费用。

3. 汽车在行驶过程中遇油库则应加满油并付加油费用 A 。

4. 在需要时可在网格点处增设油库，并付增设油库费用 C (不含加油费用A )。

5. N,K,A,B,CN,K,A,B,C 均为正整数， 且满足约束: 2\leq N\leq 100,2 \leq K \leq 102≤N≤100,2≤K≤10 。

设计一个算法，求出汽车从起点出发到达终点所付的最小费用。

解法

      一看到这种用网络流解决图论的题目，我就觉得恶心，构图会很繁琐，然后又容易打错。在比赛中碰上这种题，我肯定会先跳过。。

      不说那么多，我们来讲一下解法。

      1.首先有两个东西需要我们处理，一个是当前的油量，一个是当前所用的费用，因为这道题的k（油箱最大额度）很小，只有十。所以我们就想到了以当前的油量分层。我们把第0层设为还可以走k,第1层设为还可以走k-1......那么第k层就设为还可以走0步。如下图所示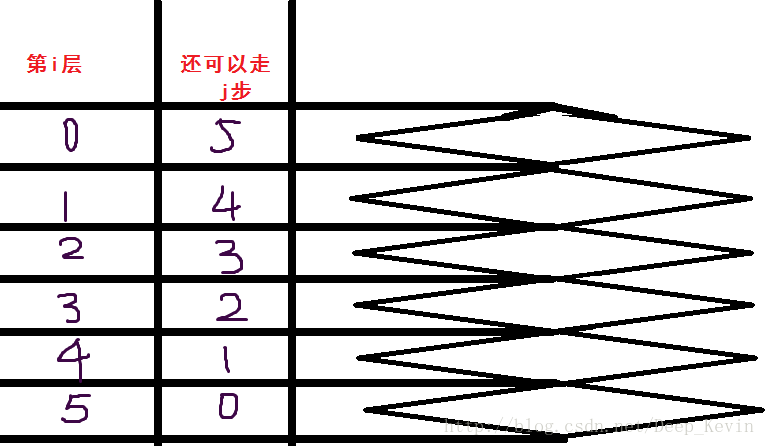

      我认真了。。】

      2.建边详情会在代码里面说，（实在是太长了。。）

      3.建完边之后，我们就按照费用流来跑SPFA，然后依次更新路径上的点，最后返回cost的和就好

（好咯，贴代码。。）

 

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<queue>
using namespace std;

int n,k,a,b,c;
struct edge{int x,y,next,cos,c;};
edge s[1000010];
int begin,end;
int every;
int len=1;
int first[110010];
int h[110010];
bool visit[110010];
int mmin[110010];
int fa[110010];

void ins(int x,int y,int c,int cos)
{
	len++;
	s[len].x=x;s[len].y=y;s[len].c=c;s[len].cos=cos;
	s[len].next=first[x];first[x]=len;
	len++;
	s[len].x=y;s[len].y=x;s[len].c=0;s[len].cos=-cos;
	s[len].next=first[y];first[y]=len;
}

bool SPFA(int &cost,int &flow)
{
	queue<int> f;
	f.push(begin);
	memset(h,63,sizeof(h));
	memset(visit,false,sizeof(visit));
	mmin[begin]=1000000000;
	h[begin]=0;
	visit[begin]=true;
	while(!f.empty())
	{
		int x=f.front();
		f.pop();
		visit[x]=false;
		for(int i=first[x];i!=0;i=s[i].next)
		{
			int y=s[i].y;
			if(h[y]>h[x]+s[i].cos && s[i].c>0)
			{
				fa[y]=i;
				mmin[y]=min(mmin[x],s[i].c);
				h[y]=h[x]+s[i].cos;
				if(visit[y]==false) f.push(y);
				visit[y]=true;
			}
		}
	}
	if(h[end]==1061109567) return false;
	flow+=mmin[end];
	cost+=mmin[end]*h[end];
	int now=end;
	while(now!=begin)
	{
		int i=fa[now];
		s[i].c-=mmin[end];
		s[i^1].c+=mmin[end];
		now=s[i].x;
	}
	return true;
}

int Cost_Flow()
{
	int cost=0,flow=0;
	while(SPFA(cost,flow));
	return cost;
}

int main()
{
	scanf("%d %d %d %d %d",&n,&k,&a,&b,&c);
	every=10000;
	begin=0;end=110001;
	ins(begin,1,1,0);
	for(int cent=0;cent<=k;cent++) ins(cent*every+n*n,end,1,0);\\把图分完层之后，每张图的（n,n)这个点都向汇点连一条边。
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
		{
			int x;
			scanf("%d",&x);
			int pos=n*(i-1)+j;
			if(x==1)
				for(int cent=k-1;cent>=0;cent--)
				{
					if(i>1) ins(cent*every+pos-n,pos,1,a);//这里的操作，相当于不同层的pos附近的
					if(j>1) ins(cent*every+pos-1,pos,1,a);//点向pos连一条a的边，当然，逆向走要
					if(i<n) ins(cent*every+pos+n,pos,1,a+b);//加b。（就是说到pos这个点的时候
					if(j<n) ins(cent*every+pos+1,pos,1,a+b);//满血复活了，必须要加油，花费a。）
				}
			else
			{
				for(int cent=k;cent>0;cent--) ins(cent*every+pos,pos,1,a+c);//可以选择在pos建一个
				for(int cent=0;cent<=k-1;cent++)//加油站，花费为c，加满花费为a，总共a+c。
				{
					if(i>1) ins(cent*every+pos-n,(cent+1)*every+pos,1,0);//否则就到下一层相对应
					if(j>1) ins(cent*every+pos-1,(cent+1)*every+pos,1,0);//的位置上，费用为0，
					if(i<n) ins(cent*every+pos+n,(cent+1)*every+pos,1,b);//逆向走要加费用b，到
					if(j<n) ins(cent*every+pos+1,(cent+1)*every+pos,1,b);//下一层意味着,油减少1
				}
			}
		}
	printf("%d",Cost_Flow());
}//记得数组开大一点哦！

喜欢小编的关注我哦！Tarjan会特别照料你的。