[SDOI2015]约数个数和，洛谷P3327，莫比乌斯反演+约数定理？

最新推荐文章于 2023-01-26 16:02:51 发布

原创最新推荐文章于 2023-01-26 16:02:51 发布 · 2.8k 阅读

3 ·

CC 4.0 BY-SA版权

莫比乌斯反演专栏收录该内容

12 篇文章

订阅专栏

本文深入探讨了质因数分解在算法优化中的应用，通过解析特定数学问题，介绍了如何利用质因数分解和约数性质来简化复杂度高的算法，实现高效计算。文章详细解释了算法背后的数学原理，并提供了C++代码实现，展示了如何预处理和分块计算以提高效率。

正题

题目链接点这里

题目了然：

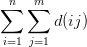
$\sum_{i=1}^n\sum_{j=1}^m d(ij)$

但我们知道 $d(ij)=\sum_{x\mid i}\sum_{y\mid j} [gcd(x,y)=1]$

为什么呢？

我们直到假如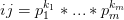 $ij=p_1^{k_1}*...*p_m^{k_m}$

那么约数个数和就是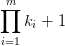 $\prod_{i=1}^m k_i+1$

考虑产生贡献的x,y是什么样子的：要不x不含a质因子，y含质因子；要不x含a质因子，y不含，要么两个都不含。

假设i里面是a质因子的指数为，j里面a质因子的指数为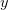，那么a质因子产生的贡献就为 x+y+1 ，就等于 k+1 。

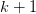根据乘法原理，算出来的数就是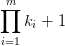 $\prod_{i=1}^m k_i+1$ 。

那么式子就变成了

$\sum_{i=1}^n\sum_{j=1}^m\sum_{x\mid i}\sum_{y\mid j}[gcd(x,y)=1] \\=\sum_{i=1}^n\sum_{j=1}^m\sum_{x\mid i}\sum_{y\mid j}\sum_{d\mid gcd(x,y)} \mu(d)\\=\sum_{d=1}^n\mu(d)\sum_{d\mid x}\sum_{d\mid y} \frac{n}{x}\frac{m}{x}\\=\sum_{d=1}^n\mu(d)\sum_{d\mid x}\frac{n}{x}\sum_{d\mid y}\frac{m}{x}$

然后发现后面的东西其实是非常规律的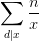 $\sum_{d\mid x} \frac{n}{x}$ ，其实就等于 $[1,\frac{n}{d}]$ 的约数个数和。

预处理一下，然后分块就行了。

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
using namespace std;

int T,n,m;
const int maxn=50000;
int mu[maxn+10],mu_sum[maxn+10];
int d[maxn+10],d_sum[maxn+10];
int p[maxn+10],temp;
bool vis[maxn+10];

int main(){
	scanf("%d",&T);
	mu_sum[1]=mu[1]=1;vis[1]=true;
	for(int i=2;i<=maxn;i++){
		if(!vis[i]) {p[++p[0]]=i;mu[i]=-1;}
		for(int j=1;j<=p[0] && (temp=i*p[j])<=maxn;j++){
			vis[temp]=true;
			if(i%p[j]==0) break;
			mu[temp]=-mu[i];
		}
		mu_sum[i]=mu_sum[i-1]+mu[i];
	}
	for(int i=1;i<=maxn;i++){
		for(int j=i;j<=maxn;j+=i) d[j]++;
		d_sum[i]=d_sum[i-1]+d[i];
	}
	long long ans=0;
	while(T--){
		scanf("%d %d",&n,&m);
		int l=1,r;
		if(n>m) swap(n,m);
		ans=0;
		while(l<=n){
			r=min(n/(n/l),m/(m/l));
			ans+=(long long)d_sum[n/l]*d_sum[m/l]*(mu_sum[r]-mu_sum[l-1]);
			l=r+1;
		}
		printf("%lld\n",ans);
	}
}