FPGA基础知识（四）：深入理解时序逻辑与组合逻辑

 《FPGA基础知识》系列导航

         本专栏专为FPGA新手打造的Xilinx平台入门指南。旨在手把手带你走通从代码、仿真、约束到生成比特流并烧录的全过程。

       本篇是该系列的第四篇内容

       上一篇：FPGA基础知识（三）：彻底理解阻塞赋值与非阻塞赋值

       下一篇：FPGA基础知识（五）：深入理解计数器——数字逻辑的时序基石

---

一 引言      

       在数字电路设计中，时序逻辑和组合逻辑是构建所有复杂系统的基础。如同阴阳两面，它们各司其职又相互配合，共同构成了现代电子设备的"思维"与"记忆"。

二  本质区别：记忆能力的有无

组合逻辑像是条件反射——它对过去"毫无记忆"：

• 输出仅取决于当前输入

• 无时钟信号控制

• 信号变化立即传播

时序逻辑则如同有经验的决策者：

• 输出取决于当前输入和过去状态

• 受时钟信号严格同步

• 状态变化发生在特定时刻

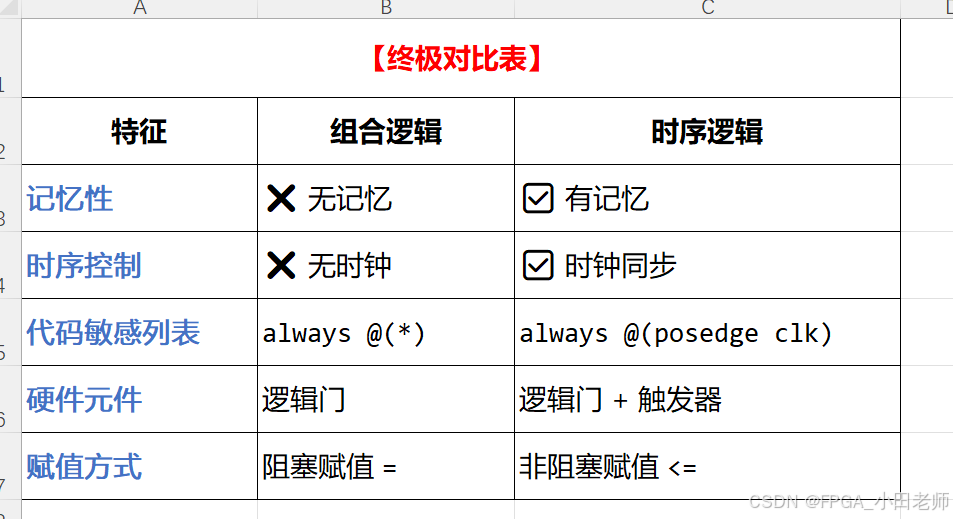
三  硬件实现的根本差异

组合逻辑由基本逻辑门直接构成：

// 组合逻辑的硬件本质就是逻辑门的连接
assign out = (a & b) | c;

时序逻辑则必须包含存储元件：

// 时序逻辑的核心是触发器
always @(posedge clk) begin
    q <= d;  // 这对应一个D触发器
end

四 实际工程中的代码体现

组合逻辑的编码风格：

// 方式一：assign语句
assign sum = a + b;
assign equal = (a == b);

// 方式二：always块
always @(*) begin
    case (sel)
        2'b00: out = a;
        2'b01: out = b;
        2'b10: out = c;
        2'b11: out = d;
        default: out = 1'bx;
    end
end

关键要点：组合逻辑必须保证所有输入信号都在敏感列表中，并且所有可能的输入组合都有明确的输出。

时序逻辑的编码规范：

// 标准的时序逻辑模板
always @(posedge clk or negedge rst_n) begin
    if (!rst_n) begin
        // 复位初始化
        count <= 8'h00;
        state <= IDLE;
    end else begin
        // 正常工作时序
        count <= count + 1'b1;
        state <= next_state;
    end
end

五 工程实践中的关键考量

时序约束的重要性
时序逻辑的性能直接由时钟频率决定，必须满足：

• 建立时间要求：数据在时钟沿前必须稳定

• 保持时间要求：数据在时钟沿后必须保持稳定

组合逻辑的潜在问题

• 毛刺现象：由于门延迟导致瞬时错误输出

• 传播延迟：限制系统最高运行频率

• 静态冒险：输入变化时可能产生干扰脉冲

六 典型应用场景

组合逻辑的适用场景：

• 算术运算单元

• 数据多路选择器

• 编码器/解码器

• 简单逻辑判断

时序逻辑的适用场景：

• 状态机实现

• 数据流水线

• 寄存器文件

• 计数器/定时器

七 混合设计：现实世界的解决方案

实际数字系统往往是时序逻辑与组合逻辑的有机结合：

module simple_cpu #(
    parameter DATA_WIDTH = 8
)(
    input wire clk,
    input wire rst_n,
    input wire [DATA_WIDTH-1:0] instruction,
    output reg [DATA_WIDTH-1:0] result
);

    // 时序部分：指令寄存器
    reg [DATA_WIDTH-1:0] instr_reg;
    always @(posedge clk or negedge rst_n) begin
        if (!rst_n)
            instr_reg <= {DATA_WIDTH{1'b0}};
        else
            instr_reg <= instruction;
    end

    // 组合部分：指令译码
    wire [3:0] opcode;
    wire [3:0] operand;
    assign opcode = instr_reg[7:4];
    assign operand = instr_reg[3:0];

    // 时序部分：执行阶段
    always @(posedge clk or negedge rst_n) begin
        if (!rst_n) begin
            result <= {DATA_WIDTH{1'b0}};
        end else begin
            case (opcode)
                4'b0001: result <= operand + result;
                4'b0010: result <= operand - result;
                // ... 其他操作
                default: result <= result;
            endcase
        end
    end

endmodule

八 设计验证与调试技巧

组合逻辑的验证重点：

• 验证所有输入组合

• 检查输出是否出现毛刺

• 确认传播延迟满足要求

时序逻辑的验证重点：

• 验证复位序列

• 检查时序约束是否满足

• 确认状态转换正确性

九 性能优化策略

组合逻辑优化：

• 逻辑门数最小化

• 关键路径优化

• 流水线技术应用

时序逻辑优化：

• 时钟域交叉处理

• 时序收敛保证

• 功耗优化考虑

---

总结与展望

      时序逻辑和组合逻辑的理解深度直接决定了数字电路设计的水平。掌握它们的特性和适用场景，能够帮助工程师：

1. 设计出更稳定可靠的电路

2. 优化系统性能和功耗

3. 快速定位和解决设计问题

4. 构建复杂的数字系统

       随着FPGA和ASIC技术的发展，对这两种基本逻辑结构的深入理解变得愈发重要。它们不仅是入门的基础，更是进阶的阶梯。

实践建议：从简单的计数器、状态机开始，逐步深入到复杂的处理器设计，在实践中不断深化对时序逻辑和组合逻辑的理解。