三维光波导加工Python脚本

import numpy as np
import matplotlib.pyplot as plt
from scipy import optimize
from mpl_toolkits.mplot3d import Axes3D

class SmoothWaveguideDesign:
    def __init__(self):
        self.n_core = 1.51
        self.n_clad = 1.45
        self.lambda0 = 1550e-9
    
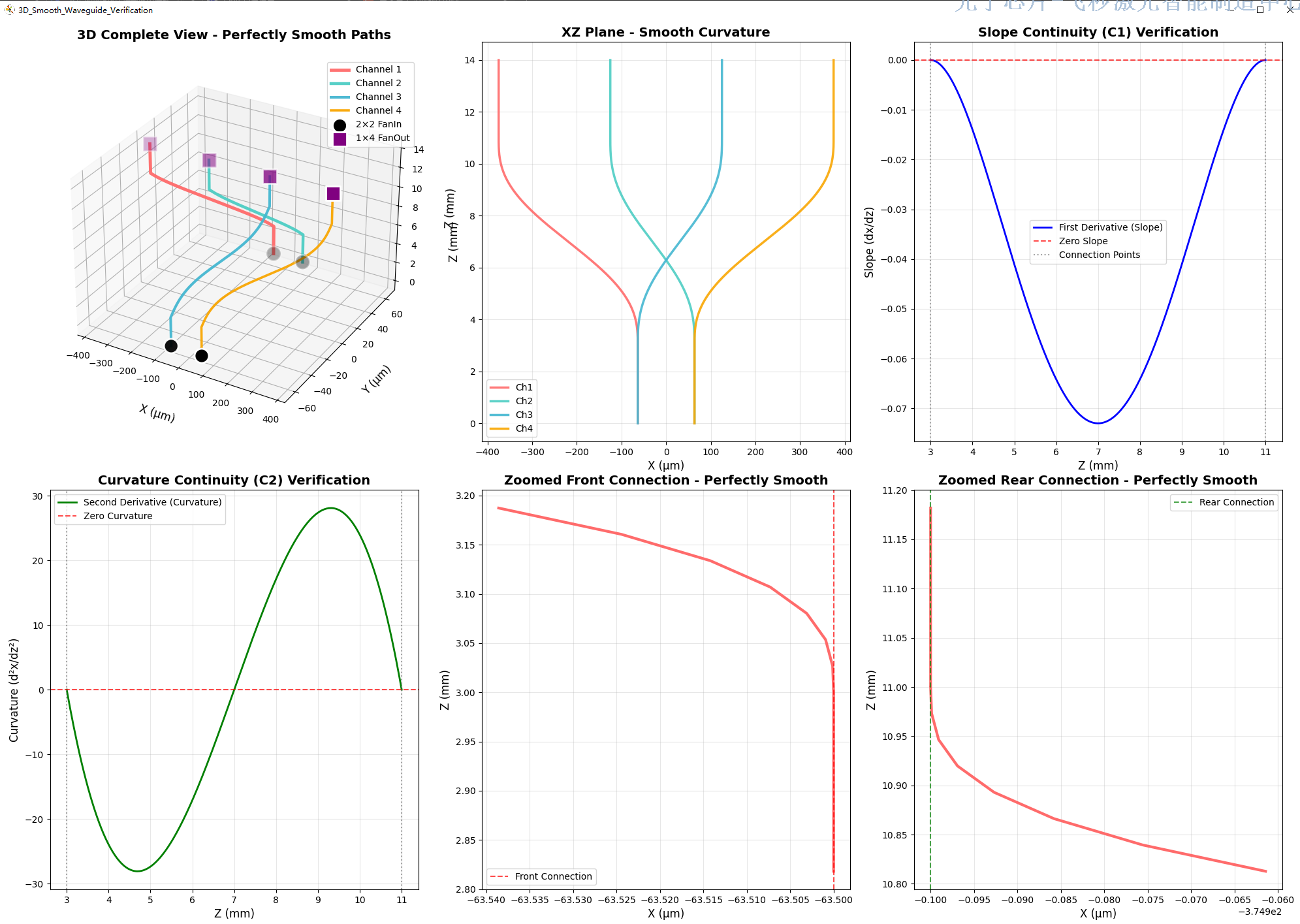
    def calculate_smooth_transition(self, x_start, z_start, x_end, z_end, y_start, y_end, transition_length):
        """Calculate smooth transition with C2 continuity"""
        # Use cubic polynomial for smooth transition
        # f(z) = a*(z-z0)^3 + b*(z-z0)^2 + c*(z-z0) + d
        z0 = z_start
        z1 = z_end
        
        # Boundary conditions for C2 continuity:
        # f(z0) = x_start, f'(z0) = 0, f(z1) = x_end, f'(z1) = 0
        # f''(z0) = 0, f''(z1) = 0
        
        # Solve cubic polynomial coefficients
        dz = z1 - z0
        dx = x_end - x_start
        
        # Cubic polynomial: f(z) = a*(z-z0)^3 + b*(z-z0)^2 + c*(z-z0) + d
        # With boundary conditions: f(z0)=x_start, f'(z0)=0, f(z1)=x_end, f'(z1)=0
        a = 2 * dx / (dz**3)
        b = -3 * dx / (dz**2)
        c = 0
        d = x_start
        
        z_transition = np.linspace(z0, z1, 200)
        z_normalized = z_transition - z0
        
        x_transition = a * z_normalized**3 + b * z_normalized**2 + c * z_normalized + d
        
        # First derivative (slope)
        dx_dz = 3 * a * z_normalized**2 + 2 * b * z_normalized + c
        
        # Second derivative (curvature)
        d2x_dz2 = 6 * a * z_normalized + 2 * b
        
        # Y coordinate varies linearly
        y_transition = y_start + (y_end - y_start) * (z_transition - z0) / dz
        
        return x_transition, y_transition, z_transition, dx_dz, d2x_dz2

def generate_smooth_waveguide_paths(input_positions, output_positions):
    """Generate perfectly smooth waveguide paths with C2 continuity"""
    num_channels = len(input_positions)
    
    # Section lengths
    straight_length = 3.0e-3
    transition_length = 8.0e-3
    total_length = straight_length * 2 + transition_length
    
    paths = []
    derivative_info = []
    
    for i in range(num_channels):
        x_in, y_in = inpu