机器学习入门——常用代价函数(Cost Function)介绍

损失函数（Loss Function ）是定义在单个样本上的，算的是一个样本的误差，而代价函数（Cost Function ）是定义在整个训练集上的，是所有样本误差的平均，也就是损失函数的平均，这给我们评价学习效果提供了一个标准，提出这个后下一步要做的就是不断优化神经网络来减小代价函数的值。

1.二次代价函数(quadratic cost)

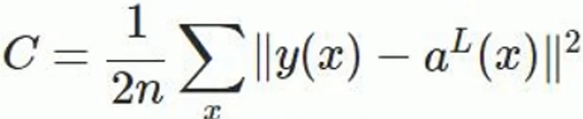
其中，C表示代价函数，x表示样本，y表示实际值，a表示输出值，n表示样本的总数。为简单起见，使用一个样本为例进行说明，此时代价函数为：

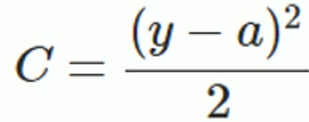
其中a=σ(z),z=ΣWj*Xj+b，σ()是激活函数。

TensorFlow中：

tf.reduce_mean(tf.square(y-prediction))

2.交叉熵代价函数(cross-entropy)

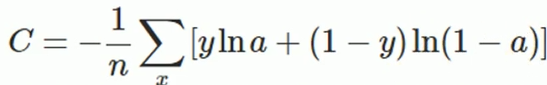
其中，C表示代价函数，x表示样本，y表示实际值，a表示输出值，n表示样本的总数。

当误差越大时，梯度就越大，参数w和b的调整就越快，训练的速度也就越快。

如果输出神经元是线性的，那么二次代价函数就是一种合适的选择。

如果输出神经元是S型函数，那么比较适合用交叉熵代价函数。

TensorFlow中：

tf.nn.sigmoid_cross_entropy_with_logits()#来表示跟sigmoid搭配使用的交叉熵。
tf.nn.softmax_cross_entropy_with_logits()#来表示跟softmax搭配使用的交叉熵。

3.对数释然代价函数(log-likelihood cost)

对数释然函数常用来作为softmax回归的代价函数，然后输出层神经元是sigmoid函数，可以采用交叉熵代价函
数。而深度学习中更普遍的做法是将softmax作为最后一层，此时常用的代价函数是对数释然代价函数。

对数似然代价函数与softmax的组合和交叉熵与sigmoid函数的组合非常相似。对数释然代价函数在二分类时可
以化简为交叉熵代价函数的形式。