变换

齐次坐标

• 齐次坐标就是将一个原本是n维的向量用一个n+1维向量来表示，是指一个用于投影几何里的坐标系统
• 齐次坐标表示是计算机图形学的重要手段之一，它既能够用来明确区分向量和点，同时也更易用于进行仿射几何变换。

向量表示和点的表示

• 一个标准的空间直角坐标系的基向量是a = (1,0,0),b=(0,1,0),c=(0,0,1)。原点为O。
• 我们可以使用基向量a,b,c来表示坐标系中任意一个向量v(vx,vy,vz)的坐标：v=vxa+vyb+vzc。
• 用基向量来表示坐标系中的任意一个点的位置，则需要考虑原点的位置，所以一个点P(px,py,pz)的坐标可以表示为：P = pxa+pyb+pzc+O。
• 点的齐次坐标表示：(x,y,z,1)，向量的齐次坐标表示：(x,y,z,0)
• 用矩阵的形式来表示的话，可以表示为

                                                   

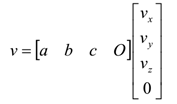
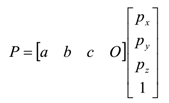
        其中最后一个0是向量标志位，1是点标志位。

• 点与点相减变为向量，因为最后一个数值变为了0。点与点相加无数学意义。

                                                               

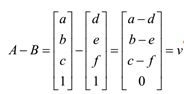
• 点与向量相加等于点，因为最后一个数值还是1，最后得到一个朝着向量方向移动了向量长度的点。
• 向量与向量相加和相减都等于向量，因为最后一个数值还是0，不过会形成新的向量。

（为什么Unity要用4*4矩阵就是这个原因，用于区分好点和向量，然后对它们进行数学运算）

 

线性变换（旋转、缩放）

线性变换：从代数上，是指可以保留矢量加和标量乘的变换。

从几何的角度上去理解，需要满足：

(1)变换前是直线的，变换后依然是直线。

(2)直线比例保持不变。

(3)变换前是原点的，变换后依然是原点

 

仿射变换（旋转、缩放、平移）

 

仿射变换，从几何的角度去理解，需要满足：

(1)变换前是直线的，变换后依然是直线。

(2)直线比例保持不变。

所以，平移、旋转、缩放都属于仿射变换

• 仿射变换可以用矩阵和向量相乘的方式来表示。计算一个点或者一个向量，经过平移、旋转、缩放等仿射变换后的值
• 一个三维的变换可以表示为：

                                                     

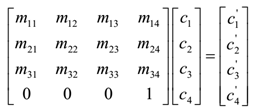
2D变换

• 平移

       2D平移矩阵：

                                                         

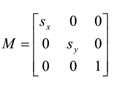
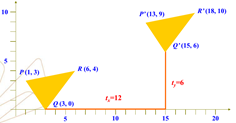
        将一个点P（x,y,1）平移(tx,ty)单位到点P＇，则P＇（x+tx,y+ty,1）

• 缩放

       2D缩放矩阵：

                                                     

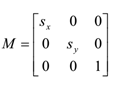
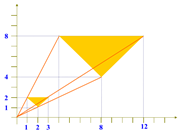
若sx=4,sy=4，点P（2,1,1）缩放后的坐标P＇（2*sx，sy，1）。向量也一样

• 旋转

       2D旋转矩阵：

                                        

 

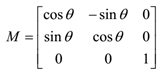
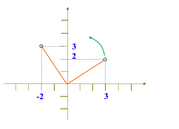
2D变换矩阵的逆矩阵

•平移矩阵的逆矩阵:

                              

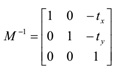
•缩放矩阵的逆矩阵:

                             

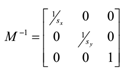
•旋转矩阵的逆矩阵:

                            

 

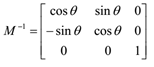
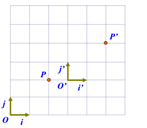
物体变换和坐标系变换

物体变换：

        

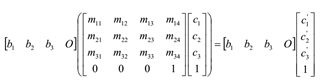
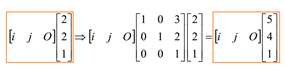
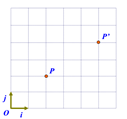
坐标系变换：

     

 

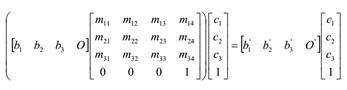
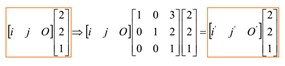
3D变换

• 平移

       3D平移矩阵：

                         

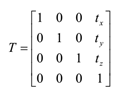
• 旋转

       3D缩放矩阵：

                           

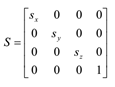
• 缩放

       3D旋转矩阵：

                         X轴                                          Y轴                                            Z轴

                                          

 

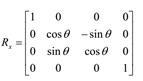
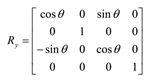
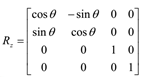
Unity中的变换

•在Unity中，我们可以使用Matrix4x4.Translate创建一个平移矩阵。

•在Unity中，我们可以使用Matrix4x4.Rotate创建一个旋转矩阵。

•在Unity中，我们可以使用Matrix4x4.Scale创建一个缩放矩阵。

•在Unity中，我们可以使用Matrix4x4.TRS创建一个移动、旋转、缩放的复合矩阵

•在Unity中，我们可以使用Matrix4x4.MultiplyPoint或者Matrix4x4.MultiplyPoint3x4来变换一个点。

•在Unity中，我们可以使用Matrix4x4.MultiplyVector来变换一个向量。