1.高斯消元法简介
2.行阶梯形
3.三大合法操作
4.高斯消元法实战演练
5.判断方程组的解
1.高斯消元法简介
高斯消元法用于解决线性方程组, 通过一系列"合法"的操作, 将一个复杂的方程组化简为一个非
常简单, 一眼就能看出解的方程组; 这个"非常简单"的形态叫做"行阶梯形"
2.行阶梯形
如下是行阶梯形:
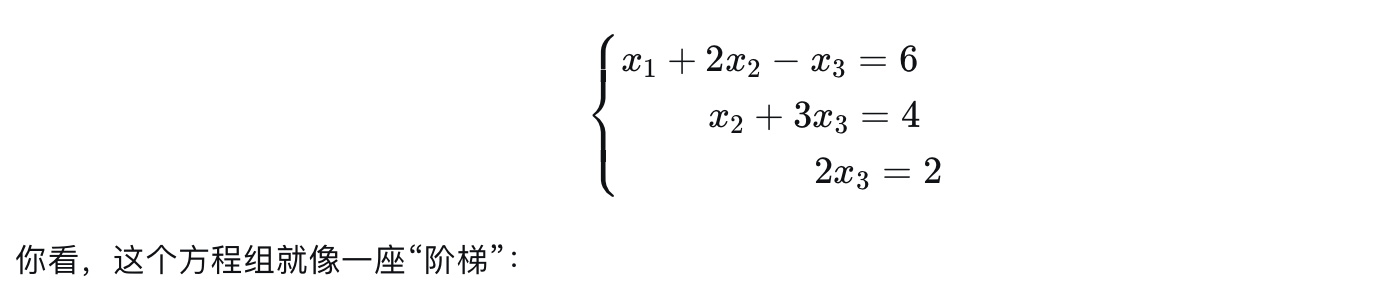
a.非零行在全零行上面
b.每一行的第一个非零数字(称为主元), 其位置总比上一行的主元更靠右
c.主元所在的列, 其他元素全是0
3.三大合法操作
三种行初等变换(不会改变改变方程组的解)
a.交换: 交换两个方程的位置, 用于将重要的方程(主元不为零)换到上面来
b.倍乘: 用一个非零常数乘以某个方程, 用于将主元的系数化为1
c.倍加: 将一个方程的若干倍加到另一个方程上
通常情况下, 我们不直接写方程组, 而是把它写成增广矩阵的形式:
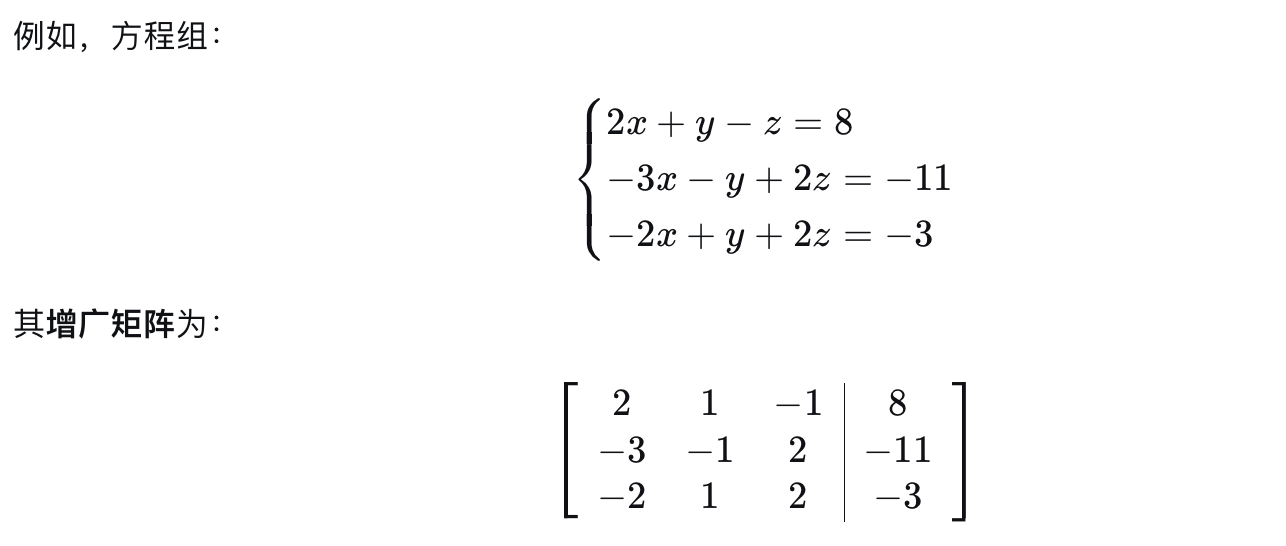
4.高斯消元法实战演练
1).处理第一列(让第一列主元下方的元素全为0)
a.为了让计算简单, 我们希望主元是1; 可以将第一行乘以1/2或者直接使用倍加; 这里我们通
过行交换和倍加来消元
b.将第一行乘以3/2加到第二行: R2 = R2 + (3/2)R1
c.将第一行乘以1加到第三行
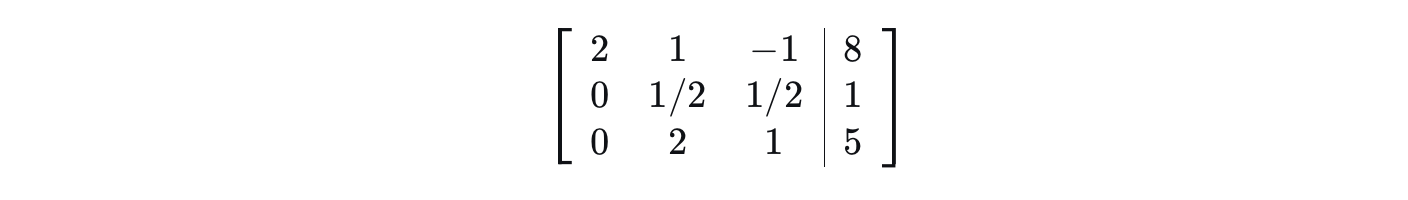
2).处理第二列(以第二行第二列为主元,将其下方元素变为0)
a.为了让主元为1, 将第二行乘以2: R2 = 2 * R2
b.将第二行乘以-2加到第三行
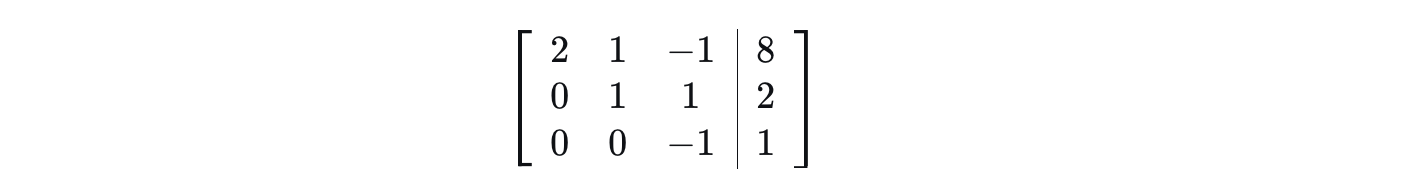
3).回代求解
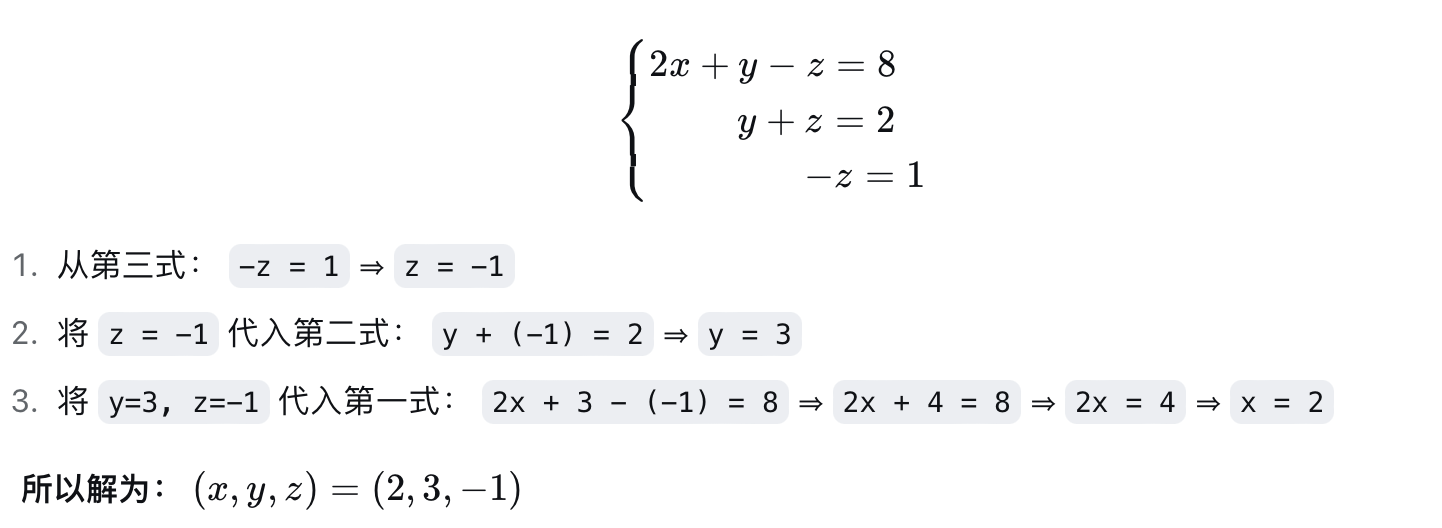
5.判断方程组的解
a.若主元的数目等于未知数的个数, 则有唯一解
b.若主元的数目小于未知数的个数
- 最后一行全是0, 则无穷解
- 出现矛盾方程, 则无解
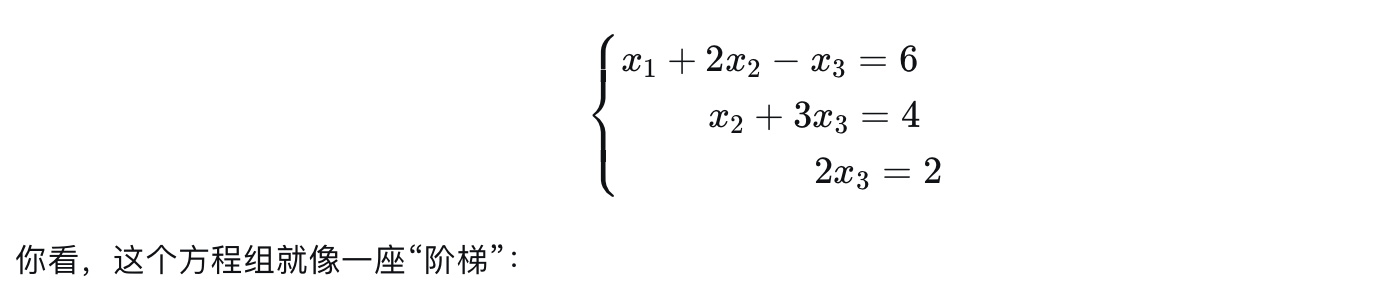
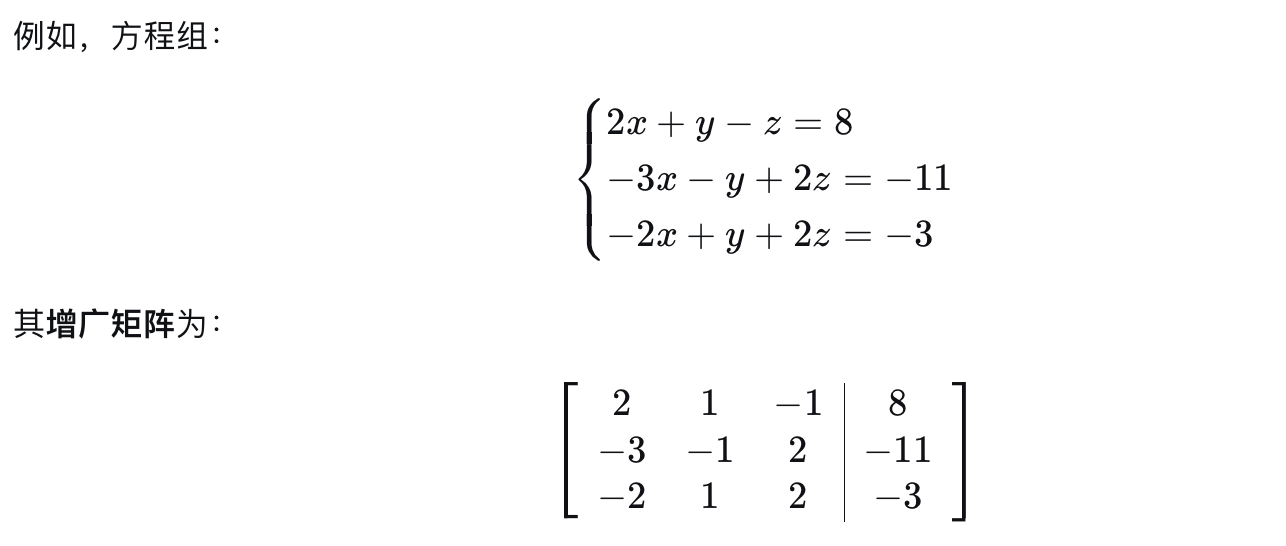
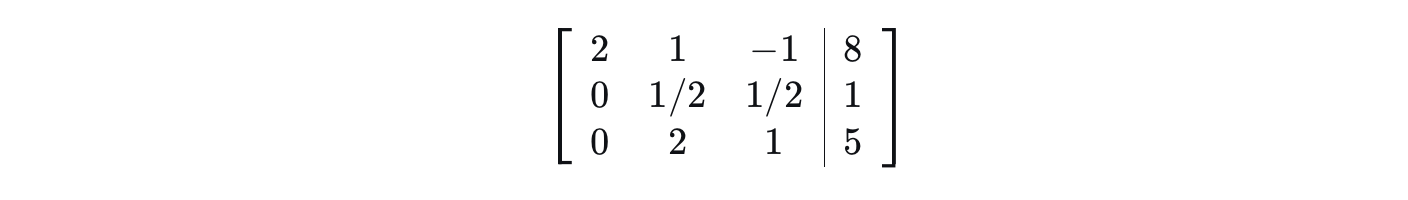
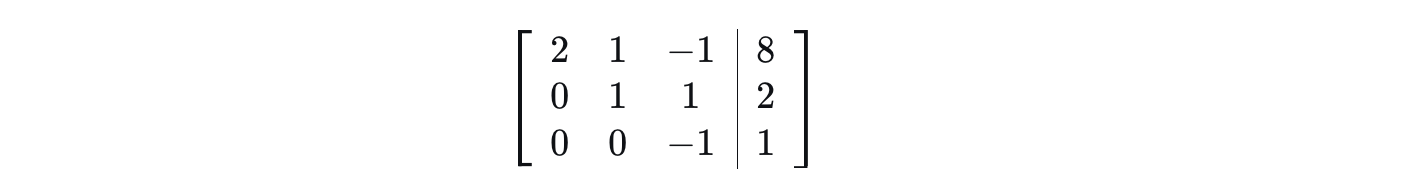
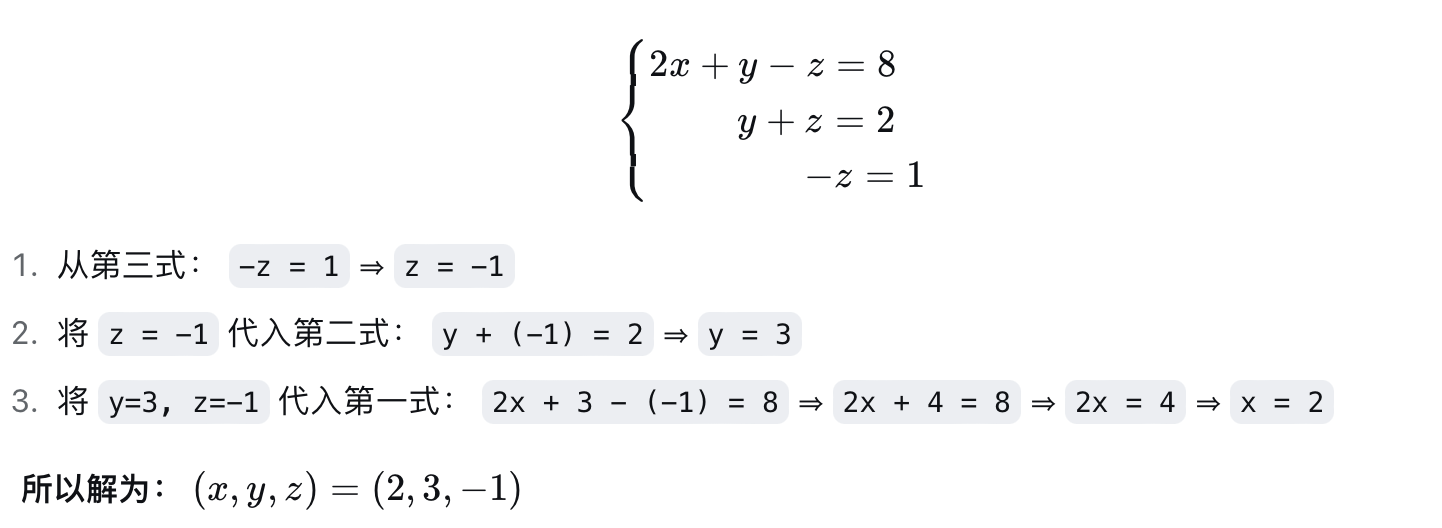





















 1355
1355

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








