向量空间（一）矩阵应用与分析 国科大

需要提前了解一下线性相关与线性无关

向量空间的作用在于将一系列用于共同性质的对象放在一起研究，是线性代数中统一研究各类线性结构框架。向量空间其实是一个满足特定要求的集合。

向量空间的定义

如果这个集合中的所有向量都满足以上10条要求，那么这个集合中的所有向量构成了一个向量空间，下面总结一下这10个要求：

1、首先是封闭性，该集合中任意的加法运算和数乘运算都必须是封闭的，即这两种运算得到新向量必须还是这个集合中的一个元素。

2、满足交换律、结合律，数乘分配律，加法存在零向量和相反向量，数乘存在单位元。

向量空间中的向量是一个广义的定义，并不是说构成向量空间的集合中的元素必须全部是向量，只要一个集合满足上述10条要求，就可以说这个集合构成了一个向量空间。

所有的对称矩阵能构成一个向量空间吗？ （对）

所有的非奇异矩阵（可逆矩阵）构成一个向量空间吗？ （错）

子空间

如果一个向量空间的非空子集中的所有元素也满足加法和数乘在该子集中封闭，那么称该子集是原向量空间的子空间。例如：对于一个三维空间xyz，xOy排名的所有向量构成一个向量空间，这个向量空间是三维空间的向量空间的子空间。

三维空间中的任意平面都是其子空间吗？ （错）

三维空间中的任意过原点平面都是其子空间吗？ （对）

三维空间中的任意曲面都是其子空间吗？ （错）

三维空间中的任意过原点曲面都是其子空间吗？ （错）

张成空间

如果一组线性无关的向量的线性组合可以表示这个向量空间中的任意向量，那么就称这组向量张成了这个向量空间。

这个概念保证了两点：1、一组线性无关的向量，就保证了没有冗余，或者说最小的线性组合。2、可以表示向量空间的任意向量，保证了其代表性，是最能表示这个向量空间的组合。

实际上，一个向量空间可以由多组线性组合张成（其实就是一个向量空间不同的基）但是一旦线性组合选定，那么这个向量空间中所有向量的表示方法就唯一确定了（其实就是线性方程组何时有唯一解的问题）。

张成空间还可以很好的描述向量空间的子空间。例如上图，去掉这个线性组合中的一个向量，那么剩余的向量就张成了原空间的子空间。

张成集

这个定义很简单，构成张成空间的若干向量构成的集合，就称为张成集。一个张成空间可以有多个张成集，就跟一个向量空间可以有多个基一样。

子空间的和

如果X和Y分别是向量空间V的子空间，那么它们的和也是向量空间V的子空间。

如果分别是张成向量空间X和Y的张成集，那么的并集也是X+Y的张成集。

矩阵的行空间和列空间

矩阵A的列空间是其列向量张成的空间，即矩阵向量乘积Ax所构成的集合。

矩阵A的行空间是其行向量张成的空间，也可以看成的列向量张成的空间。

子空间与线性函数的关系

线性函数的值域（记作）就是一个矩阵的列空间，简单证明一下线性函数运算的封闭性：

也可以说，每个子空间都是某个线性函数的值域。

我们可以发现，子空间和线性函数值域是等价的。这里还有一个问题，线性函数值域和子空间等价，那么和谁的子空间等价呢？这里是一个我之前不太了解的概念，这里以我的理解简单分享给大家：

线性函数的值域是其陪域（codomain） 的子空间。陪域是指一个函数（映射）中，目标元素所在的集合，简言之，陪域是函数 “可能输出” 的集合范围，值域是 “实际输出” 的集合（是陪域的子集）。例如：

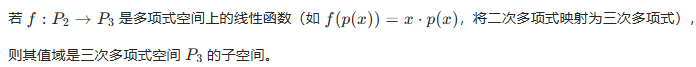
零空间与左零空间

齐次线性方程组的解集构成了矩阵A的零空间。记作

齐次线性方程组的解集构成了矩阵A的左零空间。记作

零空间是矩阵A作用下 “映射到零向量” 的输入向量集合。

总结

主要讲了四个子空间：

• 列空间：矩阵的列向量能组合出的所有向量，就像这些列向量 “张成” 的一片空间；
• 行空间：矩阵的行向量能组合出的所有向量，是行向量的 “张成空间”；
• 零空间：能让矩阵 “把向量变成零向量” 的那些输入向量，也就是方程的所有解；
• 左零空间：类似零空间，但针对矩阵的转置，是方程 的所有解。

它们本质上都是由主元列（基础解系）张成的，这里解释一下左零空间是如何张成的：

第四点的详细证明如下：

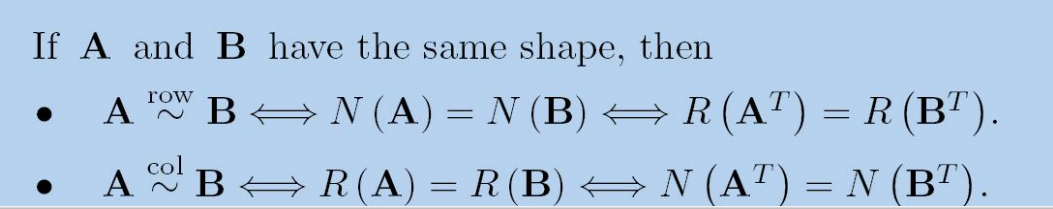
这些还揭示了矩阵行/列等价的本质是它们的行/列空间是否相同

证明逻辑在于行最简型的唯一性，而行最简形的非零行向量是原矩阵行空间的一组基。行空间相同的矩阵，其行最简形必相同，因此可通过行变换互相转化。零空间相同的矩阵，其行最简形也相同，因此行等价。

行空间相同即行等价的证明如下：