线性变换（二）矩阵分析与应用国科大

原创于 2025-11-03 20:54:57 发布 · 1.4k 阅读

CC 4.0 BY-SA版权

文章标签：

回忆

上一篇文章证明了所有有限维下的线性变换可以构成一个向量空间，并找出了这个向量空间的基，其证明的关键在于构造 $\mathbf{B_{ji}}$ ，它的作用是将向量空间L中的u向量的第j个系数与向量空间V中第i个基向量相乘，这个构造看起来非常奇怪，但它确实是我们想找的基向量，这个构造是如何想到的呢？

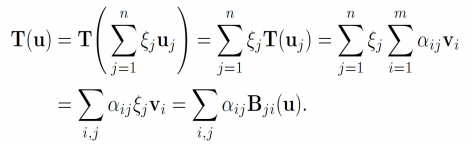
这一步是证明基向量张成性的关键步骤，我们从这里来看这个构造是怎么来的

先将u向量由向量空间L的基表示，再根据线性变换的可加性和齐次性（数乘封闭）将T放入求和中，再将 $\mathbf{T}(\mathbf{u_j})$ 由向量空间U的基表示，再根据乘法分配律展开。

到这里 $\sum_{i,j} \alpha_{ij} \xi_j \mathbf{v}_i$ ，我们注意这个形式， $\alpha_{ij} \xi_j \mathbf{v}_i$ ，这里其实我们已经用一组 $\alpha_{ij}$ 来作为线性表出的系数， $\xi_j \mathbf{v}_i$ 作为线性无关的一组基，这时我们将 $\xi_j \mathbf{v}_i$ 定义为 $\mathbf{B_{ji}}$ ，称 $\mathbf{B_{ji}}$ 为线性变换空间的基。因此这一构造方法其实是从结果倒退得到的，直接想是非常不容易想到的。

线性变换的坐标矩阵表示

下面我们理解一下这个公式是如何找出线性变换的矩阵表示的，首先是定义：

特别说明一下坐标矩阵 $[\mathbf{T}]_{\mathcal{B}\mathcal{B}'}$ ，它与 $\mathcal{U}$ 中向量的坐标表示相乘后，能得到该向量在 $\mathbf{T}$ 作用后，在 $\mathcal{V}$ 基 $\mathcal{B}'$ 下的坐标表示。这个 $[\mathbf{T}]_{\mathcal{B}\mathcal{B}'}$ ，就是我们想找到的，而它可以由以下公式计算得到：

$[\mathbf{T}]_{\mathcal{B}\mathcal{B}'} = \left( [\mathbf{T}(\mathbf{u}_1)]_{\mathcal{B}'} \mid [\mathbf{T}(\mathbf{u}_2)]_{\mathcal{B}'} \mid \cdots \mid [\mathbf{T}(\mathbf{u}_n)]_{\mathcal{B}'} \right)$

这个公式比较抽象，所以我先通过一个具体的例子来介绍计算的过程，最后再给出这个公式的推导。

如何求解坐标矩阵

来看这样一个例子，线性变换 $\mathbf{T}$ 做了这样一个事情：将二维空间的向量按某种规则映射到三维空间，下面尝试求解线性变换对应的矩阵：

这个过程是好理解的，那么我们由一个特例求解出的 $[\mathbf{T}]_{\mathcal{B}\mathcal{B}'}$ ，是否对这个向量空间中其它向量的线性变换的坐标表示也有效呢？首先我们验证一下：

这个过程是比较好理解的，计算过程也并不复杂（如果你对线性代数中的过度矩阵还有印象，这个求解过程其实是类似的，某种程度上坐标矩阵和过度矩阵是非常类似的，只不过坐标矩阵研究不同向量空间，而过度矩阵研究同一空间的不同基，后续我们会重新介绍过度矩阵，将其称为基变换矩阵），但其只是一个特例，为了保证不失一般性，我们还要通过一个抽象的线性变换来进行证明：

证明：

在例子中，我们通过步骤2计算得到了坐标矩阵，证明中相当于省去了这一步，直接得到结果并拼接起来。下面我们需要证明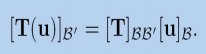，即坐标矩阵与u向量在 $\mathcal{B}$ 中的坐标的乘积，等于u向量在 $\mathcal{B'}$ 中的坐标：

至此，我们完成了线性变换的矩阵表示，即证明了坐标矩阵和线性变换的一致性，具体定义如下：

微分算子

解释一下这个例子：

这里如果你理解不了为什么坐标表示是这样，可以回看前一个例子，实际上就是用待定系数法求解方程组。我以第一个为例简单说明一下：

，设 $a*1+b*t+c*t^2+d*t^3=0$ ，解得a=1，b=c=d=0，其余三个同理。下面我们验证求解的坐标矩阵是否正确：

线性变换的复合与坐标矩阵的乘法

这个证明过程是根据线性函数的性质来说明的，图中的推导过程非常明确，不再赘述

考虑这样一个问题：线性变换复合后对应的坐标矩阵是如何变换的呢？

这一结论表明，先做 $\mathbf{T}$ 变换再做 $\mathbf{L}$ 变换，等价于 “先做 $\mathbf{T}$ 的坐标矩阵乘法，再做 $\mathbf{L}$ 的坐标矩阵乘法。

线性变换与矩阵代数的联系

这里我证明一下第三点，它说明了如何某个线性变换是可逆的，那么这个线性变换的逆的坐标矩阵等同于线性变换的坐标矩阵求逆大家可以自己找一个具体的例子试一试：

坐标矩阵的表示本质上依赖于基的选择。同一个线性变换，在不同基下的坐标矩阵形式会不同。某些基可能会让坐标矩阵呈现 “特殊形式”（如对角矩阵），但这些形式并非变换本身的特性，而是基的选择导致的。因此，我们需要脱离特定基，直接研究线性变换本身的固有性质。我们需识别那些在所有基下都保持不变的坐标矩阵性质（如秩、行列式、特征值等）。这些性质是线性变换内在的、固有的，与基的选择无关。下次我们会继续讨论这个问题。