线性变换（三）矩阵分析与应用国科大

原创已于 2025-11-10 14:14:19 修改 · 891 阅读

10 ·

CC 4.0 BY-SA版权

文章标签：

#机器学习 #算法 #人工智能 #矩阵

于 2025-11-06 15:59:54 首次发布

写这一篇主要是在完成作业（四）时对符号产生了很多疑问，因此补充这篇文章来辨析一下几个矩阵，找几个例子算一算这几个矩阵会理解的更好

1、线性变换在基下的矩阵表示 $[\mathbf{T}]_{\mathcal{B} }$

例如，如果把前文提到的伸缩变换记为 $\mathbf{T}(\mathbf{u})=\mathbf{v}$ (即将u向量伸缩为v向量），可以在标准基 $\mathcal{B}$ 下表示为矩阵 $[\mathbf{T}]_{\mathcal{B} }$ ，使得 $\mathbf{v}=[\mathbf{T}]_{\mathcal{B} }*\mathbf{u}$

再例如：

这个例子中，我们已知向量空间中的一组基 $\mathcal{B}$ ，线性变换 $\mathbf{P}$ 将 $\mathbf{u}$ 向量变为了 $\mathbf{P}(\mathbf{u})$ ，这个过程，就是在求解线性变换 $\mathbf{P}$ 在基 $\mathcal{B}$ 下的矩阵表示 $[\mathbf{P}]_{\mathcal{B} }$

2、基变换矩阵（过度矩阵） $\mathbf{P}$

基变换矩阵的作用是将一个向量在一组基下的坐标表示变成另一组基下的坐标表示，如果你记得线性代数中的过度矩阵，这两者实际上是一样的。下面看一个例子来理解这个过程：

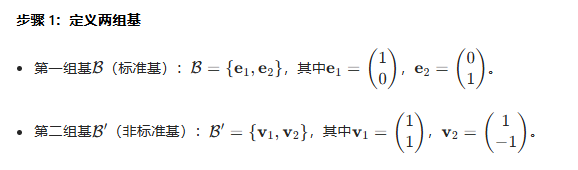
3、线性变换的坐标矩阵 $[\mathbf{T}]_{\mathcal{B} \mathcal{B'} }$

这个前文中已经举了非常多的例子，仅从计算求解的角度来说，基变换矩阵和线性变换的坐标矩阵的求解过程是非常类似的。不同的地方总结如下：

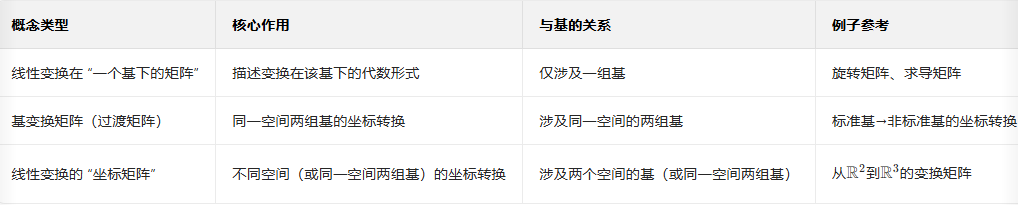
此外，还有一点值得强调：线性变换会把一个向量变成另一个新向量（除了恒等变换），而基变换并不会改变向量，只是改变了其坐标表示。这是其最大的不同。

基变换和线性变换的联系

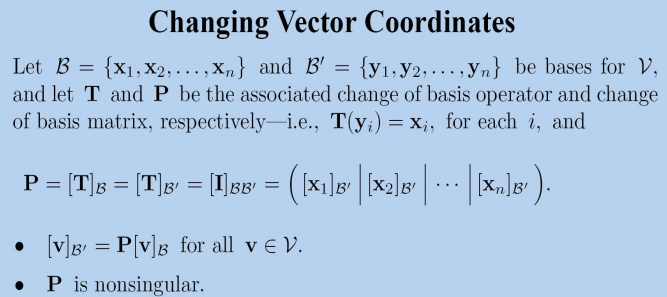
这个公式说明，如果我们定义一个线性变换 $\mathbf{T}(\mathbf{y_{i}})=\mathbf{x_{i}}$ 做了这样一件事：把一个向量在基 $\mathcal{B'}$ 下的坐标 $\mathbf{y_{i}}$ 变成了在基 $\mathcal{B}$ 下的坐标 $\mathbf{x_{i}}$ ，那么基变换矩阵 $\mathbf{P}$ 就等价于线性变换 $\mathbf{T}$ 在基 $\mathcal{B}$ 下的矩阵表示 $[\mathbf{T}]_{\mathcal{B} }$ ，同时也等价于线性变换 $\mathbf{T}$ 在基 $\mathcal{B'}$ 下的矩阵表示 $[\mathbf{T}]_{\mathcal{B'} }$ ，还等价于恒等变换 $\mathbf{I}$ 在基对 $(\mathcal{B}, \mathcal{B}')$ 下的坐标矩阵 $[\mathbf{I}]_{\mathcal{B}\mathcal{B}'}$ 。

下面我们证明一下中间的公式

这里我在补充一下

为什么基变换矩阵 $\mathbf{P}$ 等于线性变换 $\mathbf{T}$ 在基 $\mathcal{B}$ 下的矩阵表示 $[\mathbf{T}]_{\mathcal{B} }$ ，这个其实由 $\mathbf{P}$ 的定义可以得到：

为什么基变换矩阵 $\mathbf{P}$ 等于恒等变换 $\mathbf{I}$ 在基对 $(\mathcal{B}, \mathcal{B}')$ 下的坐标矩阵 $[\mathbf{I}]_{\mathcal{B}\mathcal{B}'}$ ？

线性变换是将一个向量空间中的向量变换到另一个向量空间中，而恒等变换 $\mathbf{I}$ 保证了线性变换前后的向量是同一个向量（只是在不同的基下的坐标表示不同了），而这恰好就是基变换的定义， $[\mathbf{I}]_{\mathcal{B}\mathcal{B}'}$ 的列向量是 $\mathcal{B'}$ 中每个向量在基 $\mathcal{B}$ 下的坐标。~~具体的推导比较繁琐，感兴趣可以去问问AI。~~推导如下：

基变换矩阵 $\mathbf{P}$ 描述了 “将 $\mathcal{B}'$ 的基向量用 $\mathcal{B}$ 的基向量表示” 的过程，而恒等变换 $\mathbf{I}$ 在基对 $(\mathcal{B}, \mathcal{B}')$ 下的矩阵，恰好记录了 $\mathcal{B}'$ 的基向量经 $\mathbf{I}$ （即保持不变）后在 $\mathcal{B}$ 下的坐标”，两者本质上是同一过程的不同表述，因此等价。