我会先通过几个例子来帮助大家理解线性变换的过程,之后证明所有固定线性变换构成的向量空间的基是什么。
线性变换
线性变换是一种特殊的变换:把一个向量变为另一个向量,把一个空间变到另一个空间,这个过程就能成为变换,如果这个变换能再满足一些特殊的要求,就可以把这个变换称为之线性变换。例如,求导的过程把变换到
,这是一个典型的线性变换。
简单线性变换
1、伸缩 

2、翻折 

3、关于x轴对称 

4、逆时针旋转


通过这几个例子可以看到,“变换”这一过程是非常抽象的概念,但我们可以通过矩阵来描述一些特殊的变换,包括投影、旋转、对称等一系列几何变换在内,都可以通过矩阵来为其定义一个通用的、求解变换后结果的方法。(大家可以回忆一下中学,如果要求解一个向量旋转之后得到的新向量,我们大概率只能通过三角函数来画图慢慢推导;但有了矩阵之后,只需要在该向量左乘旋转矩阵,就可以直接得到变换后的向量了)
线性变换的定义


指的是将一个在向量空间U中的向量x,通过线性变换T,映射到V空间,记为
。
类似之前提到的线性函数,线性变换也需要满足加法和数乘封闭的要求。
线性变换是一个矩阵吗?
不是。线性变换是一种映射关系,而矩阵只是这种映射的表示(准确来说,是映射在某个基下的特定表示)。同一线性变换在不同基下的矩阵表示不同,但变换本身的 “线性性质” 和 “映射效果” 不变。并非所有线性变换都能用矩阵表示,但有限维空间上的线性变换必然存在矩阵表示。

坐标与基

线性变换空间的基
根据之前学过的向量空间可以知道,向量空间其实是一个满足特定要求的集合。既然线性变换可以将一个向量映射为另一个向量,那么所有的线性变换是否构成一个向量空间呢?(这里的线性变换指固定向量空间之间的变换,主要是为了严谨,因为不限定定义域和目标空间的线性变换是无法构成向量空间的)如果是,那么线性变换空间的基又是什么呢?
其实由线性变换的定义就可以看出,它一定可以构成一个向量空间的,毕竟线性变换就是根据线性函数定义的,它必然满足加法和数乘封闭。

那么线性变换空间的基是什么(假设基为)


这里用一个具体的例子来帮助理解的作用



我们可以看到,通过,成功的将一个三维空间中的向量u映射到了四维空间V上。同样的对于每个向量u的三个坐标,都可以映射到四维空间V的四个基向量上,所有这样的变换总共有3×4=12个。总得来说,
的作用是将u向量的第j个系数与向量空间V中第i个基向量相乘,请牢记这个作用。
要证明是线性变换的基,需要证明构成这个基的向量线性无关且可张成整个空间。
证明线性无关,根据线性无关的定义,即如果,那么只有
时,这个式子才会成立。

的作用是将向量
的系数与四维空间V的基向量
相乘,由于
是基向量,
![]() ,当j ≠ k时,
,当j ≠ k时,均为0。

到这样就证明了是线性无关的。
证明可张成整个空间
,回顾张成的定义:
对于任意的,都存在
使得


即写作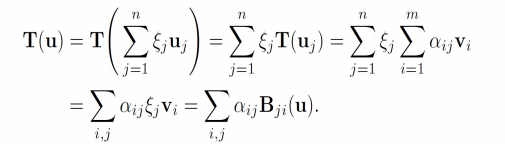
这样解释一下这个连等式:
第一个等号:向量u可以由向量空间U的基向量唯一表示。
第二个等号:利用线性变换的可加性和齐次性(数乘封闭)。这个等号,可以通过数学归纳法证明,我补充在文章最后。
第三个等号:是
映射到向量空间V中的向量v,可以由V的基向量唯一表示。
第四个等号:乘法分配律
第五个等号:乘法交换律+的定义
所以
至此,我们证明了的线性无关和张成性,也就证明了
是整个线性变换空间的基。这个证明过程,需要牢记
的作用是将u向量的第j个系数与向量空间V中第i个基向量相乘。这种构造方式不容易理解。
空间的维度由
基向量的个数决定,由
的构造方法可以知道其维度为
补充
证明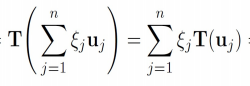

由数学归纳法




















 1495
1495

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








