模与内积（七）

原创于 2025-11-24 21:07:04 发布 · 555 阅读

3 ·

CC 4.0 BY-SA版权

文章标签：

#人工智能

上一篇文章讲到了反射矩阵和旋转矩阵，由于考试将近，这里先跳过了课件中的快速傅里叶变换域卷积（考试不考，而且我想花时间把这点单独写一篇文章）

上三角化求解最小二乘

对于不相容线性方程组 Ax=b（即该方程组无解），最小二乘问题的目标是找到 x，使得残差 ε=Ax−b 的欧氏范数平方最小。

通过正交矩阵 $\mathbf{P}$ （前面提到过，正交矩阵是 “保范数” 的等距变换，即 $\|\mathbf{P}\boldsymbol{y}\| = \|\boldsymbol{y}\|$ ）对 $\mathbf{A}$ 做正交约简，将 $\mathbf{A}$ 化为上梯形矩阵 $\mathbf{T}$ ：

也就是之前QR分解的过程。

同时，对常数项 $\boldsymbol{b}$ 做同样的正交变换：

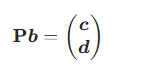
利用正交矩阵的保范性，残差的范数平方可转化为：

由于 $\|\boldsymbol{d}\|^2$ 是与 $\boldsymbol{b}$ 无关的常数，要最小化 $\|\boldsymbol{\varepsilon }\|^2$ ，只需最小化 $\|\mathbf{R}\boldsymbol{x}-\boldsymbol{c}\|^2$ 。

而 $\mathbf{R}$ 是上三角矩阵， $\|\mathbf{R}\boldsymbol{x}-\boldsymbol{c}\|^2$ 最小当且仅当 $\mathbf{R}\boldsymbol{x}=\boldsymbol{c}$ 。

因此，原方程组 Ax=b 的最小二乘解，等价于上三角方程组 Rx=c 的解

四种上三角化方式的数值稳定性对比

1. Householder/Givens 约简（QR 分解）：稳定

原理：正交矩阵 $\mathbf{Q}$ 是保范的，浮点误差 $\mathbf{E}$ （ $\mathbf{Q}$ 的误差）、 $\mathbf{F}$ （ $\mathbf{R}$ 的误差）不会放大。
推导：近似分解 $\tilde{\mathbf{A}} = (\mathbf{Q}+\mathbf{E})(\mathbf{R}+\mathbf{F}) \approx \mathbf{A} + \mathbf{Q}\mathbf{F} + \mathbf{E}\mathbf{R}$ ，由于 $\|\mathbf{Q}\mathbf{F}\| = \|\mathbf{F}\|$ 、 $\|\mathbf{E}\mathbf{R}\| \leq \|\mathbf{E}\|\|\mathbf{R}\|$ ，误差项的量级与 $\mathbf{A}$ 相当，因此 $\tilde{\mathbf{A}} \approx \mathbf{A}$ ，算法稳定。

2. 高斯消元（LU 分解）：不稳定（除非完全选主元）

无选主元 / 部分选主元：浮点误差下，近似分解 $\tilde{\mathbf{A}} = (\mathbf{L}+\mathbf{E})(\mathbf{U}+\mathbf{F}) \approx \mathbf{A} + \mathbf{L}\mathbf{F} + \mathbf{E}\mathbf{U}$ 。若 $\mathbf{L}$ 或 $\mathbf{U}$ 的元素远大于 $\mathbf{A}$ ，误差项 $\mathbf{L}\mathbf{F}$ 、 $\mathbf{E}\mathbf{U}$ 会被放大，导致结果偏离原矩阵。
完全选主元：可控制 $\mathbf{U}$ 的元素增长（理论上 $\mathbf{U}$ 的元素不超过 $\gamma = n^{1/2}(2^{1}3^{1/2}\dots n^{1/(n-1)})^{1/2}$ ，这里的证明比较繁琐，不再说明），此时算法稳定，但完全选主元计算成本高。

3. Gram-Schmidt（QR 分解）：分情况

作为 QR 分解算法：经典 / 改进 Gram-Schmidt 均不稳定（误差会积累）。
作为最小二乘求解算法：改进 Gram-Schmidt 是稳定的（误差传播被约束）。

总结

我们可以看到，尽管有非常的求解线性方程组的方式，我们最开始接触到的高斯消元仍然是最快的算法。

互补子空间

设 $\mathcal{X}, \mathcal{Y}$ 是向量空间 $\mathcal{V}$ 的子空间，若满足：

$\mathcal{V} = \mathcal{X} + \mathcal{Y}$ （空间的和，即 $\mathcal{V}$ 中任意向量可表示为 $\mathcal{X}$ 与 $\mathcal{Y}$ 中向量的和）；
$\mathcal{X} \cap \mathcal{Y} = \{\mathbf{0}\}$ （交为零向量，即分解唯一）。

则称 $\mathcal{X}$ 与 $\mathcal{Y}$ 是互补子空间，此时 $\mathcal{V}$ 称为 $\mathcal{X}$ 与 $\mathcal{Y}$ 的直和，记为 $\mathcal{V} = \mathcal{X} \oplus \mathcal{Y}$

若 $\mathcal{X}$ 的基为 $\mathcal{B}_\mathcal{X}$ ， $\mathcal{Y}$ 的基为 $\mathcal{B}_\mathcal{Y}$ ，则以下陈述等价：

$\mathcal{V} = \mathcal{X} \oplus \mathcal{Y}$ ；
$\mathcal{V}$ 中任意向量v可唯一分解为 $\mathcal{V} = \mathcal{X} + \mathcal{Y}$ （其中 $\boldsymbol{x}\in\mathcal{X}$ , $\boldsymbol{y}\in\mathcal{Y}$ ）；
$\mathcal{B}_{\mathcal{X}} \cap \mathcal{B}_{\mathcal{Y}} = \emptyset$ （基向量无交集），且 $\mathcal{B}_\mathcal{X} \cup \mathcal{B}_\mathcal{Y}$ 是 $\mathcal{V}$ 的一组基。

以 $\mathbb{R}^3$ 为例：

取 $\mathcal{X}$ 为 “过原点的平面”（2 维子空间）；
取 $\mathcal{Y}$ 为 “过原点且不在 $\mathcal{X}$ 内的直线”（1 维子空间）。

此时 $\mathcal{X} + \mathcal{Y} = \mathbb{R}^3$ ，且 $\mathcal{X} \cap \mathcal{Y} = \{\mathbf{0}\}$ ，因此 $\mathcal{X}$ 与 $\mathcal{Y}$ 是互补子空间， $\mathbb{R}^3 = \mathcal{X} \oplus \mathcal{Y}$

投影

在模与内积（五）中讲正交投影矩阵时，有提到过投影的理解

现在再从互补子空间的角度理解投影：

已知向量空间 $\mathcal{V} = \mathcal{X} \oplus \mathcal{Y}$ （ $\mathcal{X},\mathcal{Y}$ 是补子空间），则对任意 $\mathbf{v} \in \mathcal{V}$ ，存在唯一分解 $\mathbf{v} = \mathbf{x} + \mathbf{y}$ （ $\mathbf{x} \in \mathcal{X}, \mathbf{y} \in \mathcal{Y}$ ）：

$\mathbf{x}$ 称为 $\mathbf{v}$ 沿着 $\mathcal{Y}$ 投影到 $\mathcal{X}$ 的投影向量；
$\mathbf{y}$ 称为 $\mathbf{v}$ 沿着 $\mathcal{X}$ 投影到 $\mathcal{Y}$ 的投影向量。

投影的分类：

正交投影（Orthogonal Projection）：若 $\mathcal{X} \perp \mathcal{Y}$ （即 $\mathcal{X}$ 与 $\mathcal{Y}$ 是正交补子空间），此时的投影就是 “正交投影”（符合几何中 “垂直投影” 的直观概念）。
斜投影（Oblique Projection）：若 $\mathcal{X}$ 与 $\mathcal{Y}$ 不是正交补子空间，此时的投影称为 “斜投影”。

从我们之前学到的投影矩阵来看，对于 $\mathbb{R}^n$ 中的补子空间 $\mathcal{X},\mathcal{Y}$ ，可构造投影矩阵 $\mathbf{P} \in \mathbb{R}^{n \times n}$ ，使得对任意 $\mathbf{v} \in \mathbb{R}^n$ ， $\mathbf{P}\mathbf{v}$ 恰好是 $\mathbf{v}$ 沿着 $\mathcal{Y}$ 投影到 $\mathcal{X}$ 的结果。下面我们对投影矩阵下一个定义

投影矩阵（投影算子）

设 $\mathcal{X}$ , $\mathcal{Y}$ 是向量空间V的补子空间 $\mathcal{V} = \mathcal{X} \oplus \mathcal{Y}$ ，对任意 $\mathbf{v} = \mathbf{x} + \mathbf{y}$ （ $\mathbf{x} \in \mathcal{X}, \mathbf{y} \in \mathcal{Y}$ ），定义线性算子 $\mathbf{P}$ 满足 $\mathbf{P}\mathbf{v}=\mathbf{x}$ ，则称 $\mathbf{P}$ 为沿着 $\mathcal{Y}$ 投影到 $\mathcal{X}$ 的投影算子。

投影矩阵的性质

下面解释一下为什么 $\mathbf{P}$ 的值域空间（像空间）和零空间（核空间）是这样的：

首先明确，对任意 $\mathbf{v} \in \mathcal{V}$ ，存在唯一分解： $\mathbf{v} = \mathbf{x} + \mathbf{y}=\mathbf{P}\mathbf{v}+(\mathbf{I}-\mathbf{P})\mathbf{v}$

回忆一下值域空间的定义 $R(\mathbf{A})$ :满足 $R(\mathbf{A})=\left \{ \boldsymbol{b} \mid \mathbf{A} \boldsymbol{x}=\boldsymbol{b}\right \}$ ，在线性算子 $\mathbf{P}$ 中，值域空间是所有 $\mathbf{P}\boldsymbol{v}$ 的结果构成的集合。由于 $\mathbf{P}\boldsymbol{v}=\boldsymbol{x}$ ，而 $\boldsymbol{x}$ 可以取遍 $\mathcal{X}$ 中的任意向量，因此 $R(\mathbf{P})=\mathcal{X}$ 。

零空间的定义是满足 $\mathbf{P}\mathbf{v} = \mathbf{0}$ 的所有 $\mathbf{v}$ 构成的集合。若 $\mathbf{P}\mathbf{v} = \mathbf{0}$ ，则分解式中 $\mathbf{x} = \mathbf{0}$ ，即 $\mathbf{v} = \mathbf{0} + \mathbf{y} = \mathbf{y} \in \mathcal{Y}$ ；反之，对任意 $\mathbf{y} \in \mathcal{Y}$ ，取 $\mathbf{v} = \mathbf{y}$ ，则 $\mathbf{P}\mathbf{v} = \mathbf{0}$ 。因此 $N(\mathbf{P}) = \mathcal{Y}$ 。

总上， $\mathbf{v} = \mathbf{x} + \mathbf{y}=\mathbf{P}\mathbf{v}+(\mathbf{I}-\mathbf{P})\mathbf{v}$ ， $\mathcal{V} = R(\mathbf{P}) + N(\mathbf{P})$

投影的值域空间和零空间的关系作用

设 $\mathcal{X}$ 的基构成矩阵 $\mathbf{X}$ ， $\mathcal{Y}$ 的基构成矩阵 $\mathbf{Y}$ ，则投影矩阵 $\mathbf{P}$ 可表示为：

证明如下：

如果看不懂最后的基变换，可以查看线性变换（三）——基变换矩阵

线性算子 $\mathbf{P}$ 是投影算子，当且仅当它是幂等的 $\mathbf{P}^2 = \mathbf{P}$

证明如下：

必要性（投影算子→幂等）：投影算子的定义是 “将向量分解为补子空间的和，保留目标子空间部分”，因此 $\mathbf{P}^2\mathbf{v} = \mathbf{P}(\mathbf{P}\mathbf{v}) = \mathbf{P}\mathbf{x} = \mathbf{x} = \mathbf{P}\mathbf{v}$ ，故 $\mathbf{P}^2 = \mathbf{P}$ 。
充分性（幂等→投影算子）：若 $\mathbf{P}^2 = \mathbf{P}$ ，则：
- 空间的和：对任意 $\mathbf{v} \in \mathcal{V}$ ，可分解为 $\mathbf{v} = \mathbf{P}\mathbf{v} + (\mathbf{I}-\mathbf{P})\mathbf{v}$ ，其中 $\mathbf{P}\mathbf{v} \in R(\mathbf{P})$ （值域空间）， $(\mathbf{I}-\mathbf{P})\mathbf{v} \in N(\mathbf{P})$ （零空间），故 $\mathcal{V} = R(\mathbf{P}) + N(\mathbf{P})$ ；
- 交为零向量：若 $\mathbf{x} \in R(\mathbf{P}) \cap N(\mathbf{P})$ ，则 $\mathbf{x} = \mathbf{P}\mathbf{y}$ 且 $\mathbf{P}\mathbf{x} = \mathbf{0}$ ，因此 $\mathbf{x} = \mathbf{P}\mathbf{y} = \mathbf{P}^2\mathbf{y} = \mathbf{P}(\mathbf{P}\mathbf{y}) = \mathbf{P}\mathbf{x} = \mathbf{0}$ ，故 $R(\mathbf{P}) \cap N(\mathbf{P}) = \{\mathbf{0}\}$ 。