矩阵代数（二）——LU分解矩阵应用与分析国科大

原创于 2025-10-17 09:38:58 发布 · 1.3k 阅读

13 ·

CC 4.0 BY-SA版权

文章标签：

#矩阵 #线性代数

初等变换与初等矩阵

矩阵有三种初等变换（以行为例、列同理）：

1、交换任意两行

2、某一行同乘一个不为0的数

3、某一行同乘一个不为0的数再加到零一行

三种初等变换对应了三种初等矩阵，例如我想要互换矩阵A（三阶方阵）的一二行，就可以对其左乘下图的第一个矩阵。

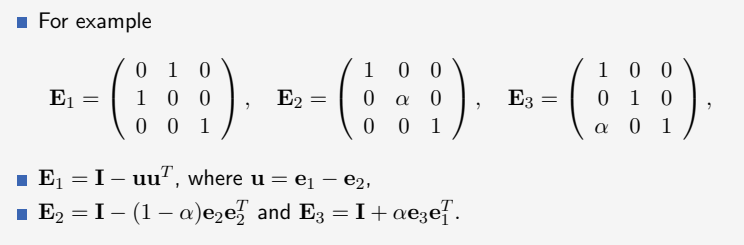
下面的两个公式是对初等矩阵进行分解，变为可以套用上一节介绍的公式（矩阵和的逆）的形式。

我多说一下如何快速看出一个初等矩阵的逆矩阵，帮助大家理解初等矩阵如何表示初等变换的。

我们根据矩阵逆的定义可以知道，如果想求上图E1的逆，那就需要找出能让它变成单位矩阵的那个矩阵，其实非常简单，只需要将它的一二行互换就可以了，如果你还记得E1的作用（左乘互换一二行），就会发现只要用E1乘以它自己就可以得到单位矩阵（左乘右乘都可以），也就是说

对于互换类初等矩阵，它的逆就是它自己

上图E2，它的作用（左乘：将第二行变为原来的α倍），如果希望它变成单位矩阵，只需要左乘一个和它一模一样的矩阵，只不过把中间的α换成1/α，也就是说

对于倍乘类初等矩阵，它的逆就是将它倍乘的那一行变为原来的倒数

上图E3，它的作用（左乘：将第一行的α倍加到第三行），如果希望它变成单位矩阵，只需要左乘一个和它一模一样的矩阵，只不过把α的位置换成-α，也就是说

对于倍加类初等矩阵，它的逆就是将它倍乘相加的数变为相反数

下面给出这三个矩阵的逆：

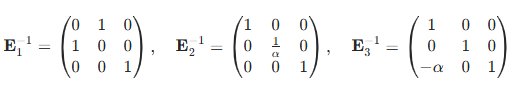
矩阵的等价

定义：如果矩阵A可以经过若干次初等行或列变换变成矩阵B，那么称A与B等价。

矩阵等价是有传递性的。

证明如下：

我们由高斯-约当消去法（就是解线性方程组，先化成上三角再把主元所在列的其余元素变为0的那个）可以知道，如果矩阵A的秩为n，那么这个矩阵一定等价于它的秩标准型 $N_{r}$ ，其中

显然可以知道，所有等价的矩阵必然有相同的秩标准型。

LU分解

U指上三角矩阵，L指下三角矩阵，凡是高斯消元法没有进行换行需求的矩阵（即不进行初等变换E1）的矩阵都可以进行LU分解。（我们后续可以通过改造这样的矩阵来使其能进行LU分解）。下面介绍LU分解的思路：

其实我们回忆一下高斯消去法，它的过程就是将一个矩阵逐渐变为一个上三角矩阵，举例：

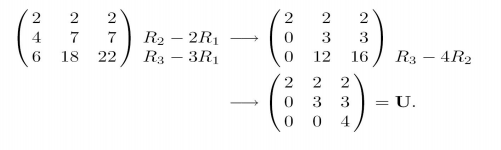
对于这样一个矩阵我们先进行两次行变换（ $-2R_{1}$ 、 $-3R_{1}$ ），再进行一次行变换（ $-4R_{2}$ ），就将其变为了一个上三角矩阵。根据我们最开始提到的，行变换实际上可以用左乘初等矩阵来描述

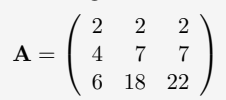
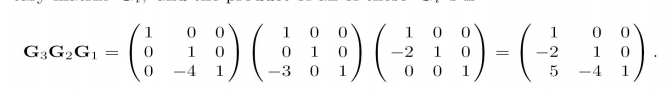
对矩阵A左乘上 $G_{3}G_{2}G_{1}$ ，就得到了上三角矩阵U。

这里大家可以自己计算一下 $G_{1}^{-1}G_{2}^{-1}G_{3}^{-1}$ （我们前面讲了如何快速求初等矩阵的逆），可以发现结果恰好是一个下三角矩阵（其实可以证明，任意下三角矩阵的乘积仍然是下三角矩阵，上三角也同理，这个是第一次作业的题）

由此可以看到：

如果 $G_{3}G_{2}G_{1}A=U$ ，那么 $A=G_{1}^{-1}G_{2}^{-1}G_{3}^{-1}U$

LU分解的计算过程是比较好理解的。这里补充一些关于上（下）三角矩阵的东西，上三角矩阵的定义是主对角线元素以下全为0的矩阵，也就是说，全0矩阵也是上（下）三角矩阵。LU分解后的两个矩阵，L矩阵的主对角线元素全为1，U矩阵的主对角线元素不为0。

LU 分解要求 L 是 “单位下三角矩阵”，其元素仅记录行倍加的乘数。但换行操作（交换两行）无法用 “行倍加变换” 表示，因此凡是需要换行的矩阵都无法进行LU分解

LU分解可以很好的求解线性方程组，因为上（下）三角矩阵都可以不通过消元来直接得出解：

这个例子可以方便大家理解上图：

LU分解的条件——方阵且顺序主子式全不为零

这里其实有一个问题，我在查资料的过程中有两种说法，第一种认为必须所有的顺序主子式都不为零，另一种认为只需要前n-1阶都不为零，这里应该是区分了标准LU分解与广义LU分解，按照课件上来说，我认为老师讲得应该是标准LU分解，即必须所有的顺序主子式都不为0。

PLU分解

有没有一个办法能让所有的矩阵都进行LU分解呢？我们之前提到了，不能进行LU分解的原因是L矩阵的元素仅能记录倍加乘数，无法记录换行，那么有没有一种方法可以记录换行呢？

比如说，我们先对A矩阵提前进行所有的行变换P，得到PA矩阵，保证其在高斯消元的过程中不出现行变换，那么PA矩阵不就可以进行LU分解了吗？但是这样有一个问题，我们如何提取知道高斯消元需要进行多少行变换呢？实际上有这样一个方法：

我们来详解这个过程，首先使用A的增广A|p来记录A矩阵的各行，p向量只参与记录行互换，不参与运算。

第一步：采用部分主元法，选择第一列中绝对值最大的元素与第一行互换，由于是互换，p向量也需要改动。

第二步：进行高斯消元，将第一列中除了4以外的所有元素都消为0，这里黑体表示的1/4，1/2，-3/4，是第二行减去第一行的1/4，第三行减去第一行的1/2，第四行加上第一行的3/4，这里为了方便后面直接写出下三角矩阵L，没有写0，而是将高斯消元的系数记录下来，减去记为正，加上记为负。这里是倍加倍减，p向量不参与运算。

第三步：继续采用部分主元法，选择第二列中除第一行外绝对值最大的元素与第二行互换，由于是互换，p向量也需要改动。

第四步：进行高斯消元，将第二列中除8、5外的所有元素都消为0，将第三行加上第二行的-1/5，p向量不参与运算。

第五步：选择第三列中的最大主元，由于其就是第三行的-6，不需要进行互换。用第四列减去第三列的1/3，p向量不参与运算。

至此，已经通过高斯消去完成了一个上三角矩阵，LU分解结束。这里计算时需要注意，黑体所写的并不是矩阵中实际的元素，只是记录高斯消去的系数方便我们写出L矩阵，它们实际上都是0。P矩阵应该是很容易根据p向量观察出来的。