解线性方程组——直接解法：LU分解、PLU分解(类似列主元消去法) | 北太天元 or matlab

文章对应视频讲解：

• PLU分解
• LU分解

---

L: lower triangular 下三角
U: upper triangular 上三角
LU 分解，顾名思义，为 把一个 矩阵 分成 一个下三角矩阵 乘上一个上三角矩阵的形式。

Example

为什么可以这样

几个基本的初等行变换，可以自己验算一下，等式的左边与右边是相等的

用上面这几个等式，重新看一下 第一个例子，

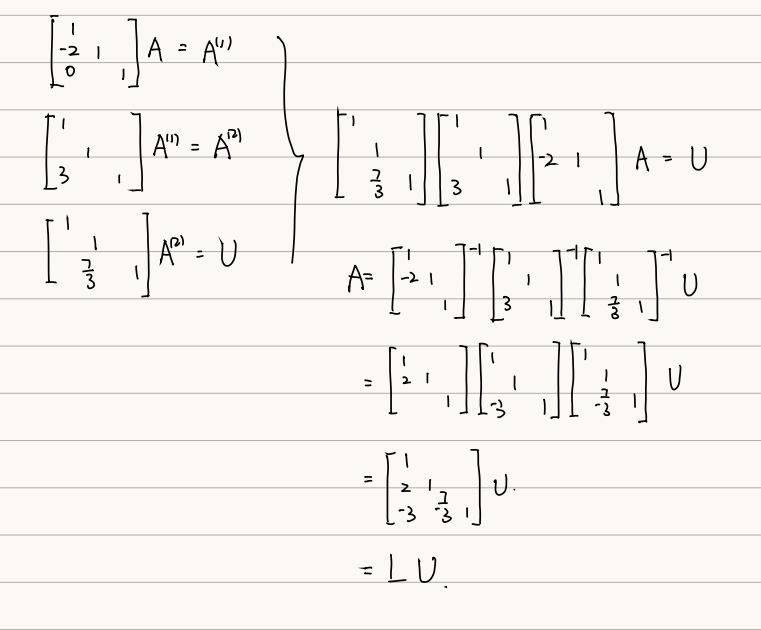
对A进行了三次行变换，得到上三角矩阵U，
两边同时左乘初等矩阵的逆，表示成 A = 啥啥啥 乘 U
再用 Fact4 和 Fact 3 得到 下三角矩阵 L

LU分解

有了这个形式后，利用矩阵相乘，元素对应相等，便可求出 L 和 U

得到 L 和 U 后，

这样便可得到 x

所以关键是怎么得到 L 和 U

计算顺序

如果自己来算
就会发现是先算出第一层，才能算出第二层，再算出第三层，等等
因为要用计算机实现，所以需要知道，具体是怎么算的


在算的过程中可以发现，只在一个矩阵 A 上便可以发生这些变化
也就不需要开 A L U 三个矩阵的存储空间

LU分解算法

先单独求出 L 和 U

这样对于 系数矩阵A 相同, 右端常数项 b 不相同的情况下,都可以使用同样的 L,U 进行计算.
所以我把这里写出单独的一步,不然也体现不出 LU 分解 的优势所在.

北太天元 or Matlab 实现

LU分解

function  [L,U] = LU_factorization(A)
% LU分解
% A ： 系数矩阵
% A = LU
%   Version:            1.0
%   last modified:      09/25/2023
n = length(A);
A([2:n],1) = A([2:n],1) * (1/A(1,1)); 
for r = 2:1:n
    for k = r:1:n
        A(r,k) = A(r,k) - A(r,[1:r-1])*A([1:r-1],k);
    end
    for m = r+1:1:n
        A(m,r) = (A(m