线性代数:矩阵的分解(LU分解n阶方阵)

矩阵分解的概念： 初中我们接触过数的分解,如:$66=3\ast 3\ast 11(质因数分解)$; 推广到矩阵，一个矩阵也可以分解为几个矩阵乘积的形式，矩阵分解具有不同的目的。

矩阵的LU分解的定义是将矩阵$A$分解为一个下三角矩阵($矩阵的有效信息都在下三角区域$)和上三角矩阵($ \small 矩阵的有效信息都在上三角区域$)乘积的方式: $\begin{array}{rl}& A=L\cdot U\end{array}$ ，其目的是为了提高计算效率。

L : Lower Triangle Matrix U:Upper Triangle Matrix
$下三角单位矩阵.$ 上三角矩阵
$\left[\begin{array}{cccc}1& 0& 0& 0\\ \ast & 1& 0& 0\\ \ast & \ast & 1& 0\\ \ast & \ast & \ast & 1\end{array}\right]\left[\begin{array}{cccc}\ast & \ast & \ast & \ast \\ 0& \ast & \ast & \ast \\ 0& 0& \ast & \ast \\ 0& 0& 0& \ast \end{array}\right]$
在LU分解中，通常将一个矩阵分解成一个下三角单位矩阵和一个上三角矩阵(不保证对角线为 $1$ )

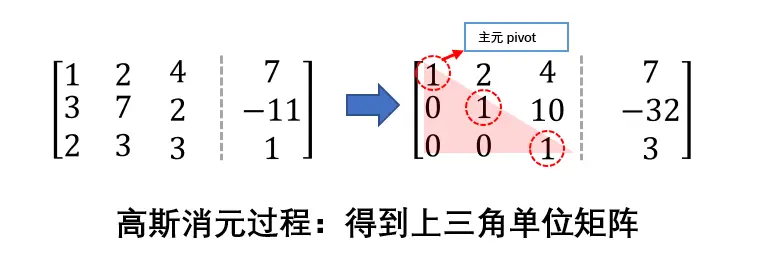
联系"高斯消元"过程: 系数矩阵和结果矩阵拼接成的增广矩阵通过一系列初等变换，就是把一个矩阵变成了上三角矩阵的过程。即 $E_p\cdot ...\cdot E_3\cdot E_2\cdot E_1\cdot A=U$
根据这条式子进行拓展有:
$\because (E_p^{-1}\cdot ...\cdot E_3^{-1}\cdot E_2^{-1}\cdot E_1^{-1})\cdot (E_p\cdot ...\cdot E_3\cdot E_2\cdot E_1)\cdot A=(E_p^{-1}\cdot ...\cdot E_3^{-1}\cdot E_2^{-1}\cdot E_1^{-1})\cdot U$
$\therefore I\cdot A=(E_p^{-1}\cdot ...\cdot E_3^{-1}\cdot E_2^{-1}\cdot E_1^{-1})\cdot U$
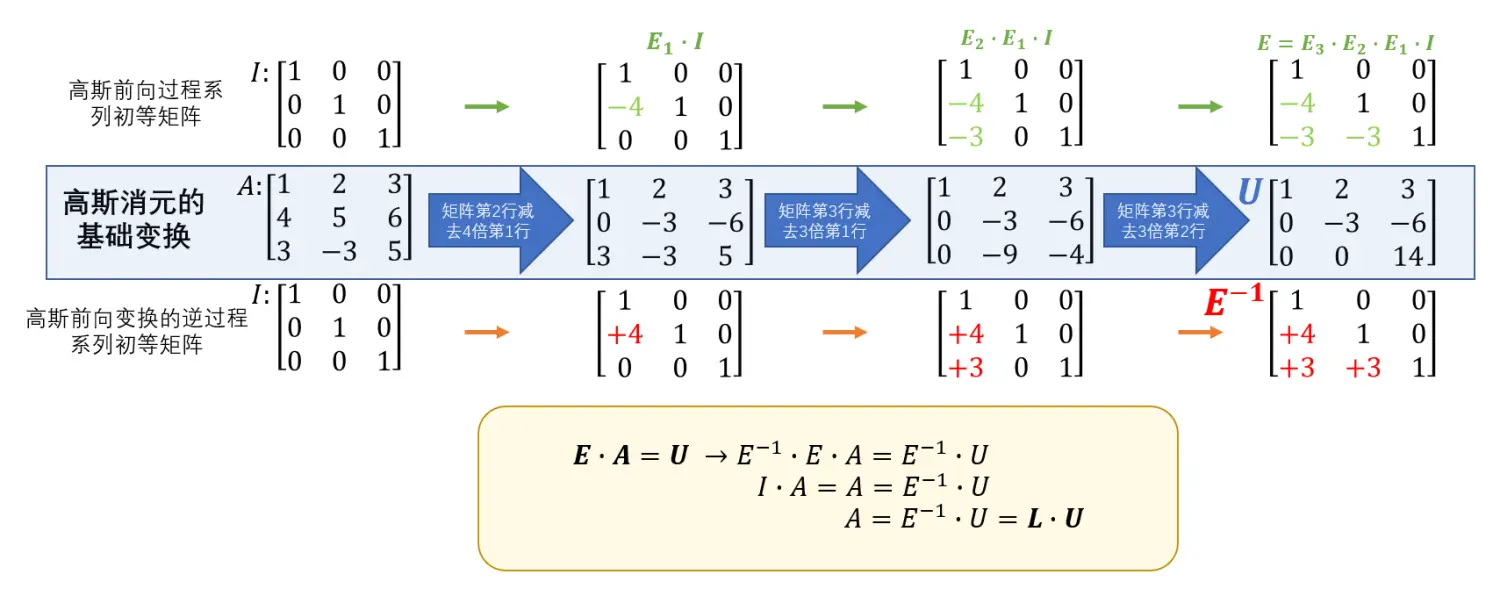
从中可以看出，高斯消元过程的逆操作变换矩阵就是下三角矩阵$L$：
$\therefore A=L\cdot U\to L=(E_p^{-1}\cdot ...\cdot E_3^{-1}\cdot E_2^{-1}\cdot E_1^{-1})$

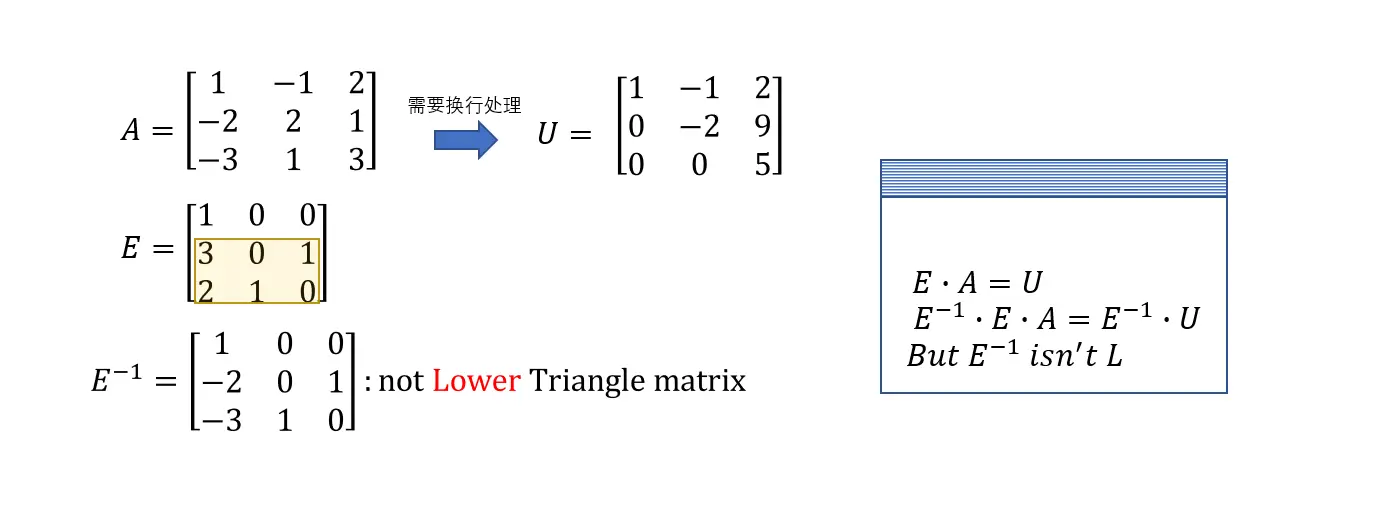
一个矩阵可以进行LU分解的前提条件：对矩阵$A$的消元过程中不能涉及行交换操作(只有主元位置为0的矩阵在高斯消元过程需要进行行变换)。因为分解得到的$L$矩阵是由单位矩阵得到的，如果消元过程发生了行交换，也就意味着单位矩阵发生了行交换，对应的L矩阵就不是一个下三角矩阵。
证明如下：

假设矩阵$A=\left[\begin{array}{cc}0& 1\\ 1& 1\end{array}\right]$可以进行LU分解。
根据LU分解的定义,则矩阵$A$可以分解得到一个下三角矩阵$L$和一个上三角矩阵$U$
$令L=\left[\begin{array}{cc}{l}_{11}& 0\\ l_{21}& l_{22}\end{array}\right]and\left[\begin{array}{cc}{u}_{11}& u_{12}\\ 0& u_{22}\end{array}\right]$
通过矩阵乘法，可以得出
$\because a_{11} = l_{11} \cdot u_{11}=0, 所以必然存在 l_{11}=0 \ 或 \ u_{11} =0 $
$如果是l_{11}=0，那么就有a_{12}=l_{11}\cdot u_{12}=0，然而这就与矩阵A中a_{12}=1的结果相矛盾$.
$如果是u_{11}=0，那么就有a_{21}=l_{21}\cdot u_{11}=0，然而这就与矩阵A中a_{21}=1的结果相矛盾$.
$\therefore \text{综上，矩阵A不能进行LU分解}$

当一个矩阵不用发生行交换进行消元过程的时候，那么对应获取它的$L$矩阵直接可以通过$E$矩阵取反得到，发生行交换后，$L$矩阵不能直接由$E$矩阵取反得到。

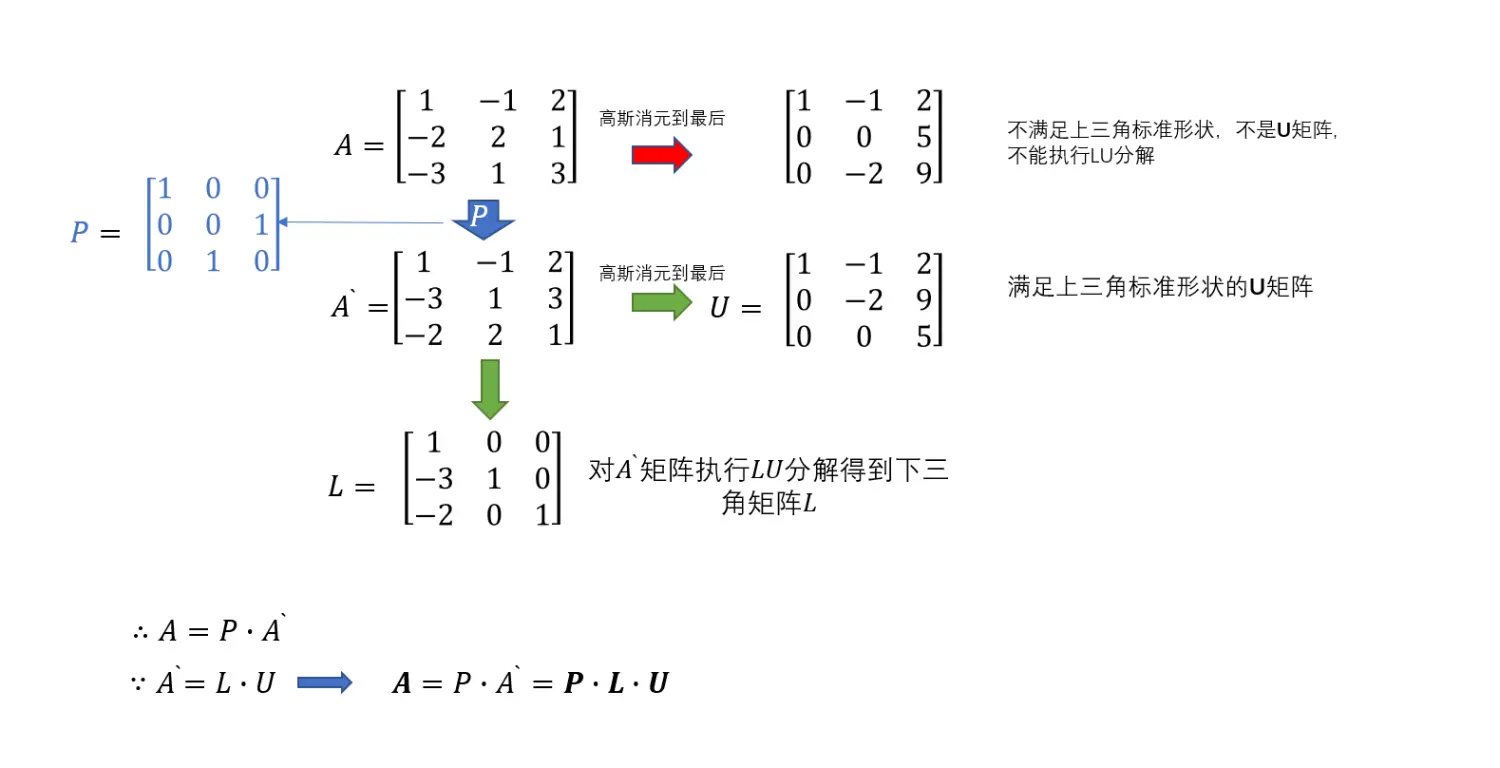
对于主元位置为零的矩阵（也就是发生行交换才能进行LU分解的矩阵，可以使用PLU分解方法$A=P\cdot L\cdot U$，P矩阵是置换矩阵）

$LU$分解的时间复杂度的计算$O(0.5n^3)$
其中$n$ 是矩阵$A_{n\ast n}$下三角区域需要化为$0$的元素的个数(一共约为$\frac{1}{2}{n}^2$个)，完成这些元素的消元约需要进行$\frac{1}{2}{n}^2$次初等变换，而每次初等变换意味着对矩阵内一行的$n$个元素都进行了一次运算，所以由$A\to U$高斯消元过程总共约发生了$0.5n^2\cdot n$次数据运算}, $O$ 时间复杂度约为 $O(0.5n^3)$。由于高斯消元过程在得到$U$矩阵的同时，每次初等变换操作的值取反往单位矩阵$I$相应的位置进行填充就可以得到$L$矩阵，所以整体上$LU$分解过程的时间消耗近乎等于 $A\to U$过程的时间。

$LU$分解加速线性系统求解

对于解线性系统$Ax=b$
$矩阵A被分解为A=L\cdot U$
$\to L\cdot U\cdot x=b$
设 $Ux=y$, 方程变为 $L\cdot y=b$ ,求出$y$的时间复杂度约为$O(n^2)$。
同样，对于$U\cdot x$,求出$x$的时间复杂度也约为$O(n^2)$
从而，将矩阵$A$通过$LU$分解，时间复杂度总体为$O(0.5n^3)+2O(n^2)$

$LU$分解计算时间复杂度相比求解矩阵的逆的过程求解$A\cdot x=b\to x=A^{-1}\cdot b$.
矩阵通过增广矩阵的形式求逆的时间复杂度为$O2n^3$，增广矩阵有$2n^2$个元素要执行消元操作。然后再求解$A^{-1}\cdot b$的时间复杂度有$O(n^2)$次操作，所以通过矩阵的逆的方法求解线性系统的时间复杂度为$O(2n^3)+O(n^2)>O(0.5n^3)+2O(n^2)$。

综上，LU分解求解线性系统的效率是比较高的。

简单LU过程的 python写法

import numpy as np
A = np.array([[1,2,3],[4,5,6],[3,-3,5]]) ### 创建一个用于分解的测试矩阵
L = [[1.0 if i==j else 0 for i in range(n)] for j in range(n)] ### 初始化L矩阵为单位矩阵
n = len(A) ### 创建变量n记录矩阵的行数
for i in range(n): #行遍历
    for j in range(i+1,n): #处理主元行下面的所有行化为0
        p = A[j][i] / A[i][i] ##求算主元行下面行主元列位置的元素是当前主元的倍数
        A[j] = A[j] - p*A[i] ##主元行下面行主元列位置的元素减去p倍主元化为0
        L[j][i] = p ### p直接填充到L矩阵
L