论文理解【Offline RL】—— 【BAIL】Best-Action Imitation Learning for Batch Deep Reinforcement Learning

• 标题：BAIL: Best-Action Imitation Learning for Batch Deep Reinforcement Learning
• 文章链接：BAIL: Best-Action Imitation Learning for Batch Deep Reinforcement Learning
• presentation：papertalk
• 发表：NIPS 2020
• 领域：离线强化学习（offline/batch RL）—— IL-based 方法

---

• 摘要：近期，DRL领域中，关于 batch RL 的研究激增。batch RL 旨在从给定的数据集中学习高性能策略，而无需与环境进行额外的交互。我们提出了一种新算法 BAIL，力求同时满足简单性和高性能。BAIL 学习一个 $V$ 函数，以此评估并选出高性能的动作，然后对这些动作数据做模仿学习来训练策略网络。利用 MuJoCo 基准任务，我们在多种批量数据集上比较了 BAIL 与其他四种 batch Q-learning 和 imitation learning 方法的性能。实验表明，BAIL 的性能远高于其他方法，并且在计算上也比 batch Q-learning 方法快得多
  

1. Offline RL 背景

• Offline RL 是这样一种问题设定：Learner 可以获取由一批 episodes 或 transitions 构成的固定交互数据集，要求 Learner 直接利用它训练得到一个好的策略，而且禁止 Learner 和环境进行任何交互，示意图如下
  
• 关于 Offline RL 的详细介绍，请参考 Offline/Batch RL简介

2. 本文方法

• 本文方法属于 IL-based 方法，适用于确定性MDP

2.1 思想

• 形式化地讲，假设对于任意 $(s,a)$ 二元组

  1. $V^{\ast }(s)$ 是最优价值函数
  2. $G(s,a)$ 代表从 $(s,a)$ 开始依照某策略行动的 return
  3. 任意满足 $G(s,a^{\ast })=V^{\ast }(s)$ 的动作即为状态 $s$ 下的最优动作

  要学习一个好的策略，等价于对 $\forall s\in \mathcal{S}$，找出对应的最优动作 $a^{\ast }$

• 本文思想很直接，分为三步

  1. 利用有限的 batch 数据，给出对最优价值函数 $V^{\ast }(s)$ 的估计 $V(s)$。为了实现这种最大化函数的估计，作者在此提出了 “上包络网络” 的概念
  2. 在 batch 中挑选那些 $G(s,a)\approx V(s)$ 的 $(s,a)$
  3. 在选出的 { ( s , a ) } \{(s,a)\} {(s,a)} 集合上做模仿学习

2.2 算法细节

2.2.1 上包络网络（upper envelope）

• 假设现有 batch 数据集 B = { ( s i , a i , r i , s i ′ ) , i = 1 , 2 , . . . , m } \mathcal{B}=\{(s_i,a_i,r_i,s_i'),i=1,2,...,m\} B={(si​,ai​,ri​,si′​),i=1,2,...,m}，假设这些数据是以轨迹形式生成并组织着的，可以计算任意状态 $s_i$ 的 MC return G i = ∑ t = i T γ t − i r t , i ∈ { 1 , . . . , m } G_i=\sum_{t=i}^T\gamma^{t-i}r_t,i \in \{1,...,m\} Gi​=∑t=iT​γt−irt​,i∈{1,...,m}（$T$ 表示 $s_i$ 所在 episode 的 horizon），从而组成状态收益集合 G = { ( s i , G i ) , i = 1 , 2 , . . . , m } \mathcal{G} = \{(s_i,G_i),i=1,2,...,m\} G={(si​,Gi​),i=1,2,...,m}

• 上包络网络：设 $V_{\varphi }(s)$ 是由参数 $\varphi =(w,b)$ 参数化的神经网络，对任意的 $\lambda >0$，若 ${\varphi }^{\lambda }$ 是以下约束优化问题的最优解，则称 $V_{{\varphi }^{\lambda }}(s)$ 是 $\mathcal{G}$ 的 $\lambda$-regularized 上包络
  $$\underset{\varphi }{\min }\sum _{i=1}^m[V_{\varphi }(s_i)-G_i{]}^2+\lambda ||w|{|}^{2}s.t.V_{\varphi }(s_i)\ge G_i,i=1,2,...,m$$ 直观地看，这个上包络网络 $V_{\varphi }(s_i)$ 的输出就是 $s_i$ 的真实 return $G_i$ 的上极限，$\lambda$ 正则项主要用于防止过拟合

• 作者对上包络网络进行了分析，假设 $V_{\varphi }(s)$ 是一个使用 ReLu 激活函数的全连接网络，给定任意 $\lambda \ge 0$，上述约束最优化问题对应的最优解为 ${\varphi }^{\lambda }=(w^{\lambda },b^{\lambda })$，使得 $V_{{\varphi }^{\lambda }}(s)$ 是数据集 $\mathcal{G}$ 的上包络网络，那么有
  ( 1 )   lim ⁡ λ → ∞ V ϕ λ ( s ) = max ⁡ 1 ≤ i ≤ m { G i }   , ∀ s ∈ S ( 2 )    V ϕ 0 ( s ) = G i   , i = 1 , 2 , . . . , m \begin{aligned} &(1)\space \lim_{\lambda \to \infin} V_{\phi^\lambda}(s) = \max_{1\leq i\leq m}\{G_i\} \space, \forall \mathcal{s\in S}\\ &(2)\space\space V_{\phi^0}(s) = G_i \space, i=1,2,...,m \end{aligned} ​(1) λ→∞lim​Vϕλ​(s)=1≤i≤mmax​{Gi​} ,∀s∈S(2)  Vϕ0​(s)=Gi​ ,i=1,2,...,m​ 可见，当 $\lambda \to \infty$ 时，网络输出为整个 batch 上的最大 return；当 $\lambda =0$ 时，如果网络容量足够，则退化为一个简单的回归情况（证明过程见原文）。因而在二者之间一定存在一个合适的 $\lambda$ 值（sweet point），使得上包络网络 $V_{{\varphi }^{\lambda }}(s)$ 能够最好地为各个状态 $s$ 估计其 return 的上极限

• 解这个约束优化问题时，作者采用了一般的方法：把 “约束转化为惩罚项”，从而将其转换为无约束优化问题，即最小化以下损失函数
  L k ( ϕ ) = ∑ i = 1 m ( V ϕ ( s i ) − G i ) 2 { 1 ( V ϕ ( s i ) ≥ G i ) + K ⋅ 1 ( V ϕ ( s i ) < G i ) } + λ ∣ ∣ w ∣ ∣ 2 L^k(\phi) = \sum_{i=1}^m\big(V_\phi(s_i)-G_i \big)^2\{\mathbb{1}_{(V_\phi(s_i)\geq G_i)}+ K ·\mathbb{1}_{(V_\phi(s_i)< G_i)}\} + \lambda ||w||^2 Lk(ϕ)=i=1∑m​(Vϕ​(si​)−Gi​)2{1(Vϕ​(si​)≥Gi​)​+K⋅1(Vϕ​(si​)<Gi​)​}+λ∣∣w∣∣2 其中 $K>>1$ 是惩罚系数，显然，当 $K\to \infty$ 时，两个优化问题同解；当 K 是一个有限值时，得到近似的上包络（存在少数 $V_{\varphi }(s_i)<G_i$），经过测试，作者在此选择了 $K=1000$

• 在四个环境中，使用含100万 transitions 的训练集学习上包络网络，结果如下（为了帮助可视化，状态按照其上包络值排序）
  
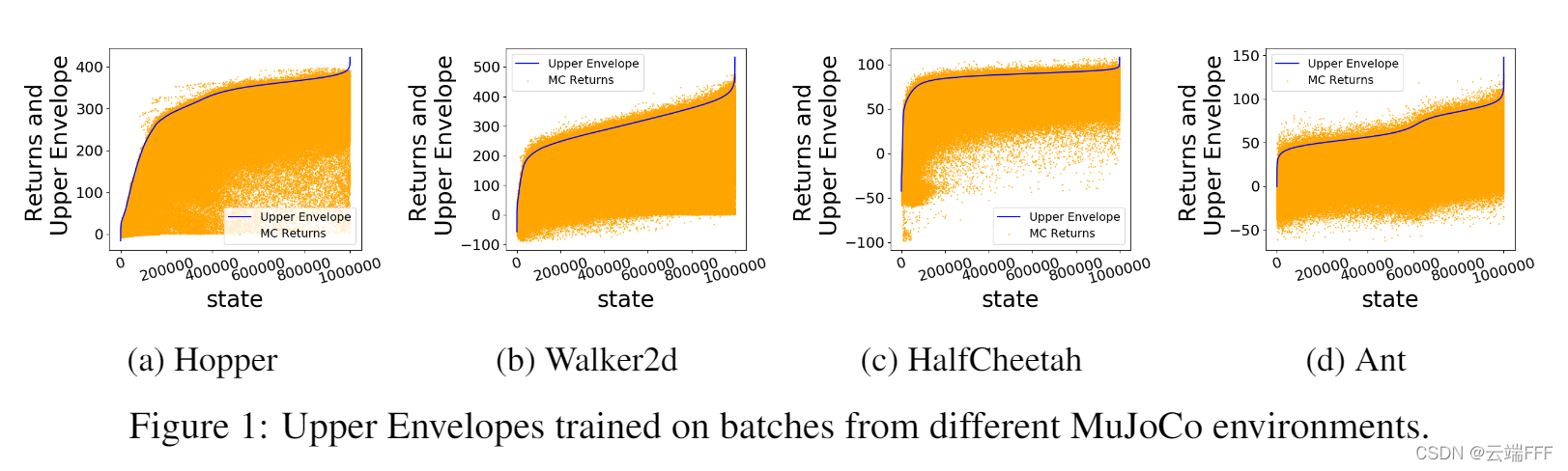
  注意这些环境都是确定性的连续控制任务，每个状态对应的动作空间是连续的，因此图中任取一列（即固定一个状态 $s$）都有很多 $(s,a)$ transition ，可见，学到的上包络网络还是比较准确的

• 另外，在实践中，作者没有使用 $L_2$ 正则项，而是使用早停来避免过拟合

2.2.2 选择最优动作

• 计算价值上包络，其实就是对数据集覆盖状态 $s$ 的最高 return 做了一个估计 $V_{\varphi }(s)$，于是可以认为，那些 return 靠近 $V_{\varphi }(s)$ 的 $(s,a)$ 二元组，其动作 $a$ 都是由 “近似最优策略” 生成的。自然地，下一步我们就要从 batch 中选出这些好的 $(s,a)$ 二元组，模仿学习以得到 “近似最优策略”

• 作者在此提出了两种最优动作选择方法

  1. BAIL-ratio：选择所有 $G_i>xV(s_i)$ 的 $(s_i,a_i)\in \mathcal{B}$，其中 $x>0$ 是一个固定常数
  2. BAIL-difference：选择所有 $G_i\ge V(s_i)-x$ 的 $(s_i,a_i)\in \mathcal{B}$，其中 $x>0$ 是一个固定常数

  其中 $x$ 是一个超参数，它和二元组的占比 $p\%$ 是一一对应的。在实践中，作者先设置比例值（比如 $p=25\%$），从而确定 $x$ 的取值。经过实验，作者发现 BAIL-ratio 方案稍好，于是选择了这种方案

• 样本点选取示意图如下
  

2.2.3 更好的收益计算方式

• 和 BCQ、BEAR 等文章一样，本文作者选用 MuJoCo 连续控制任务进行实验。这些任务是都是无限 horizon 不分幕形式的，因此训练通常的做法是：人工收集定长的交互轨迹（比如 1000 步长度），之后随机选择一个状态重新开始新轨迹。这里暗含着一个问题
  1. 无限 horizon 不分幕的任务形式，意味着轨迹都是无限长，因而每个 $(s,a)$ 或 $s$ 对应的收益都是在无限长的 episode 上计算出来的
  2. 人工划分采样轨迹长度，意味着实践中的 return 只能使用有限长度 episode 计算
• 使用有限轨迹上的 return 估计无限长轨迹上的 return，显然是不准的。虽然有折扣系数 $\gamma$，采样轨迹头部的 $(s,a)$ 计算误差较小，但是对于采样轨迹尾部的 $(s,a)$，这种误差就不能忽略了

  一个极端的例子是：设轨迹都是1000步长度，950步时某个动作使得机器人重心偏右，将在100步后摔倒，但是只过了50步这个轨迹就被打断了，因此摔倒的巨大负奖励没能传回来影响950步时这个动作的价值

• 为了缓解上述问题，作者在此提出了一个启发式的方法。设 $\epsilon \in \mathcal{B}$ 是一个轨迹，$s^{\prime }$ 是 $\epsilon$ 的最后一个状态，为了计算低 $i$ 的 transition $(s_i,a_i)$ 的 return，设 $s_j$ 是 max ⁡ { 1000 − i , 200 } \max\{1000-i,200\} max{1000−i,200} 中第一个欧式距离最靠近 $s^{\prime }$ 的状态，如下计算 return
  $$G_i=\sum _{t=i}^T{\gamma }^{t-i}{r}_t+{\gamma }^{T-i+1}\sum _{t=j}^T{\gamma }^{t-j}{r}_t$$ 可见，这个就相当于在轨迹中截取一段接在最后面。极端情况下，重新拼接后的轨迹长度也至少有 800 步（$i=1000,s_j=200$），在这种长度下，$\gamma$ 折扣后计算的 return 误差就不会太大
• 举例如下：总长度1000步，以 $s^{\prime }$ 状态终止的蓝色轨迹，为计算 $i=750$ 处 $(s_i,a_i)$ 的 return，在前 max ⁡ { 250 , 200 } = 250 \max\{250,200\} = 250 max{250,200}=250 步中找到距离 $s^{\prime }$ 欧式矩阵最近的状态 $s_j$，将 $s_i\to s^{\prime }$ 和 $s_j\to s^{\prime }$ 两段轨迹拼接在一起作为从 $s_i$ 开始的轨迹计算 return
  
• 对于这种修正方式的实验如下：该实验在 Hopper-v2 环境中进行，使用 SAC 和 DDPG 在训练中收集 batch 数据，一共训练 100 个 epochs，每个包含 100 万交互 transition。对于 BAIL，前 50 个 epochs 的交互数据用于计算上包络网络。
  
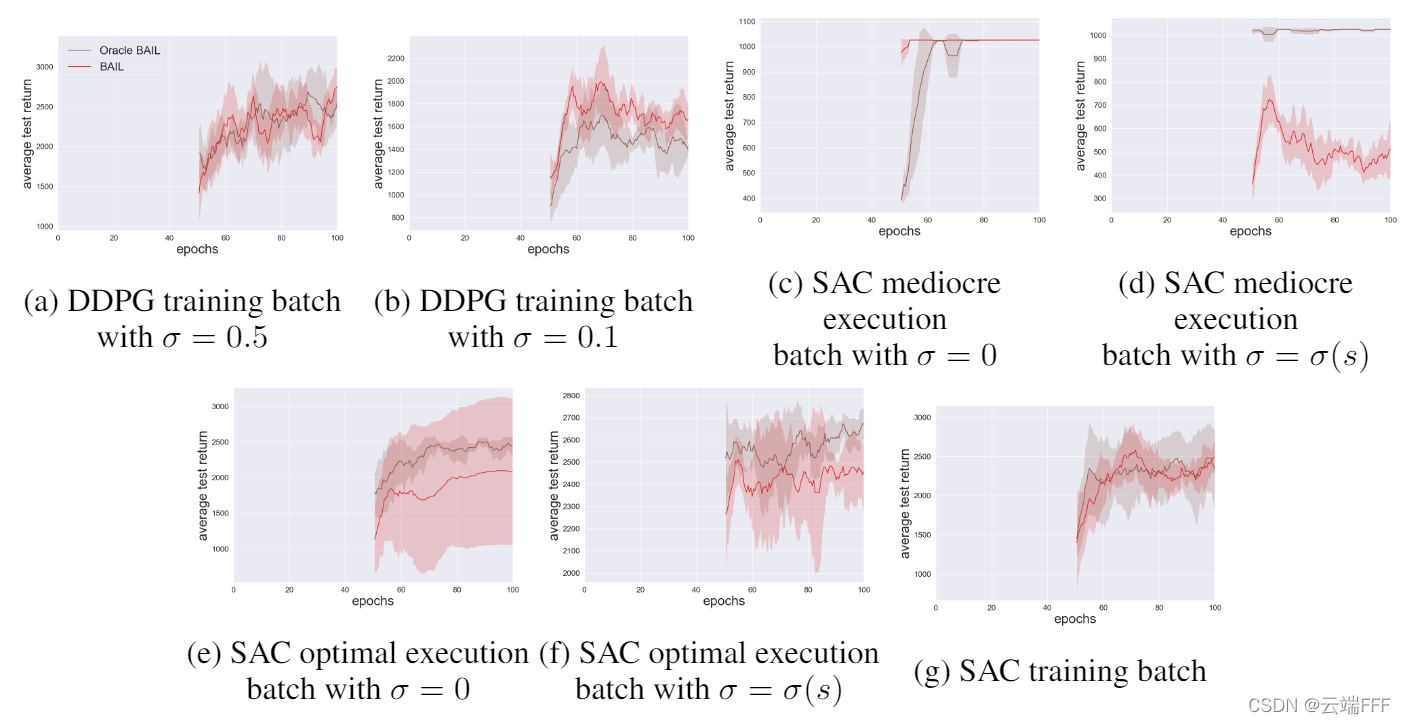
  为了评判修正 return 的准确程度，此实验中所有轨迹都运行了 2000 步，考察前 1000 步中各个 $(s,a)$ 的平均 return。红线是（BAIL）修正计算结果，棕色线（oracle）是用 2000 步计算的结果（这样每个 $(s,a)$ 至少有1000步用于计算，在折扣情况下认为是准确的），可见还是比较相似的，方法有效

2.3 伪代码

• 这里，作者使用了早停策略避免过拟合：使用参数 $\varphi$ 和 ${\varphi }^{\prime }$ 初始化两个上包络网络，

  1. $\varphi$ 使用惩罚损失训练
  2. ${\varphi }^{\prime }$ 记录迄今为止在验证集上误差最小的参数

  在每个 epoch 之后，在验证集 ${\mathcal{B}}_v$ 上计算验证损失 $L_{\varphi }$，将其与 $L_{{\varphi }^{\prime }}$ 进行比较。

  1. 若 $L_{\varphi }<L_{\varphi }^{\prime }$ ，则设置 ${\varphi }^{\prime }\leftarrow \varphi$
  2. 反之若 $L_{\varphi }>L_{\varphi }^{\prime }$，则计算这种情况连续发生的次数，连续出现 $C$ 次时训练结束，最终参数为 ${\varphi }^{\prime }$

  作者在实践中使用 $C=4$

• BAIL 的伪代码如下
  

• 上面的方法是先训练上包络网络再训练策略网络，作者也也提出了另一种同时训练两个网络的方法，如下
  
  相比而言，二者的性能差不多，但是普通 BAIL 训练速度要快一些

3. 实验

• 这篇文章做了非常多实验，事实上，他们声称详尽的实验结果也是其贡献的一部分，这里仅放出部分进行说明
• 所有实验是在 MuJoCo 环境中的连续控制任务上进行，和 BCQ 及 BEAR 论文保持一致。

3.1 生成 batch 数据

3.1.1 Training batches

• Training batches 是在强化学习算法训练过程中的交互数据组成的 bacth

  1. 使用 DDPG 在 Hopper-v2、Walker2d-v2、HalfCheetah-v2 三种环境上训练并收集数据，包含探索噪声 $\sigma =0.5$ 和 $\sigma =0.1$ 的两种情况
  2. 使用 SAC 在 Hopper-v2、Walker2d-v2、HalfCheetah-v2、Ant-v2, and Humanoid-v2 五种环境上训练并收集数据

  其中每一项，都使用不同的随机种子生成两个 batch 数据，这样一共有 $(3\times 2+5)\times 2=22$ 个 batch

• Training batches 中的数据来自从差到好的多个策略，含有很多很差的 transition，因此直接做 BC 肯定行不通

3.1.2 Execution batches

• Execution batches 是用固定策略和环境交互生成数据组成的 batch。这里作者使用了 BEAR paper 中相同的方法：先对 SAC 训练一定的次数，然后固定得到的 policy 和环境交互，得到 100万 “execution” transition 。分别在 SAC 训练到 “中等” 程度和 “最优” 程度时收集两次数据
• 在固定 policy 和环境交互时，作者考虑了带探索噪声 $\sigma (s)$ 和不带噪声的两种情况，并且对每种情况测试了两个随机种子，这样一共有 $(5\times 2)\times 2\times 2=40$ 个 batch

3.2 实验结果

3.2.1 Training batches

• 对于每个算法，训练100个 epochs（每个 epoch 由一百万 transition 组成），每 0.5 个 epochs，使用当前策略运行10个 episodes 来评估性能（对五个种子重复该过程，以获得学习曲线中显示的平均值和置信区间）
• 篇幅有限，这里仅呈现使用 DDPG，在 $\sigma =0.5$ 情况下 Training batches 的效果（对应于BCQ论文中的数据集，其余实验请参照原文支撑材料），如下
  
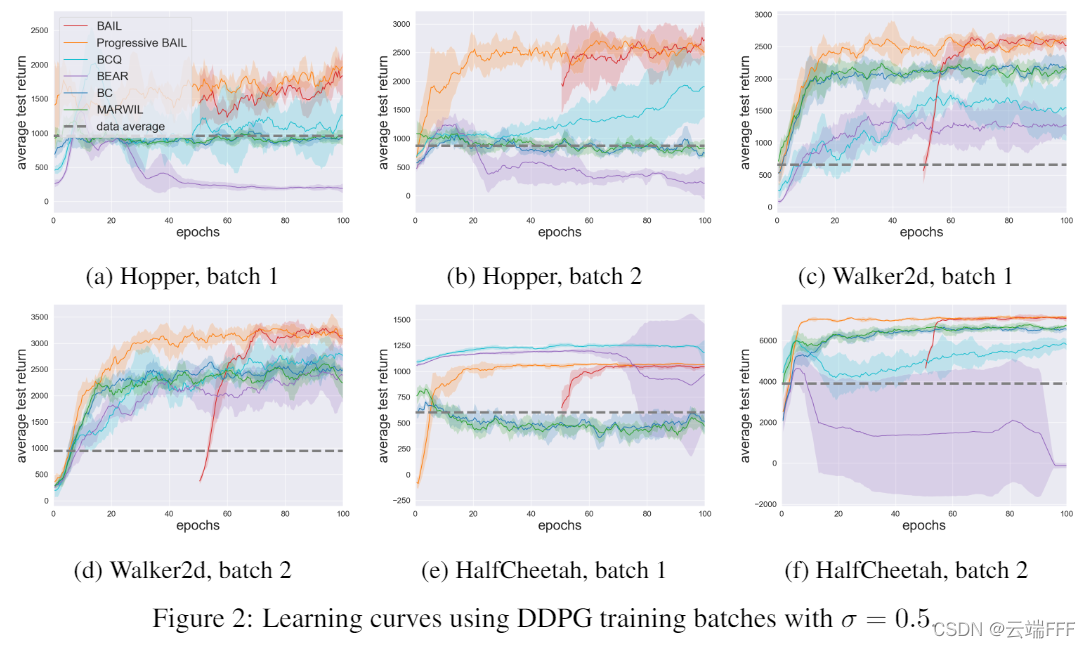
  注：BAIL 曲线从第 51 个 epochs 开始，是因为前 50 个 epochs 的交互数据用于训练上包络网络；水平灰色虚线表示 batch 中包含的 episodes 的平均收益
• 另外，对于 22 个 training batches 的测试结果如下。这里作者计算了 95.5 到 100 这最后 10 个策略的平均性能，与最高平均收益差距小于 10% 的都看作 “优胜”，以粗体表示（注：下表第7~12行对应上图；由于没有针对每个任务调节超参数，BEAR 性能较差）
  
• 可见，BAIL 在 training batches 中表现出色，有很大潜力应用于 Growing-batch RL
  1. 在 22 个 batches 上取 BAIL 性能与 BCQ、BC 性能的比率，发现 BAIL 的表现比 BCQ 好42%，比 BC 好101%
  2. BAIL对于不同的随机种子也更稳定：在22个批次中，BAIL的标准化标准差（标准偏差除以平均性能）的平均值约为BCQ的一半

3.2.2 Execution batches

• 40 个 Execution batches 上的对比结果如下
  
• 这种情况下，虽然 BAIL 仍略优于其他 Batch DRL 策略，但是 vanilla BC 显然是最强的。这是因为 batch 数据来自单个固定策略，BC很容易学习。这一结果表明，Batch DRL 的未来研究重点应放在 Training batch 或其他由不同策略收集的数据集上，因为vanilla BC 已经很好地适用于固定策略数据集

3.2.3 上包络网络消融实验

• 这部分测试上包络网络的作用。直观地看，我们要依靠上包络网络选出那些 “近似最优策略” 诱导的 $(s,a)$，从而模仿学习这个策略。如果上包络网络预测不准，那么我们就无法良好地估计近似最优动作，也就找不准 “近似最优策略” 诱导的 $(s,a)$，性能肯定会下降

• 首先，如果不学习上包络网络，直接简单地从 batch 数据集中选择相同比例的，具有最高 $G_i$ 的 $(s_i,a_i)$ 进行训练，效果如下
  
  可见，性能下降明显，因此上包络网络对于性能至关重要

• 其次，如果不训练上包络，而是简单地做个回归，效果也会变差。直观地看，假设 batch 中某状态 $s$ 对应 10 个动作，9个的 $(s,a)$ return 都是 10，另一个是20

  1. 简单回归时，$s$ 对应的 return 肯定在 10 附近
  2. 使用上包络网络，$s$ 对应的最高 return 在 20 附近

  显然，引入上包络网络后，才能更准确地选出最优 $(s,a)$ 进行模仿。实验效果也说明了这一点，如下
  

3.2.4 训练耗时

• 实验中，所有算法运行了 100 epochs，每个 batch 5个种子。每个随机种子训练耗时

  1. BAIL：1分钟∼2小时（包括上包络和模仿学习时间）
  2. Progressive BAIL：12∼24小时
  3. BCQ：36∼72小时
  4. BEAR：60∼100小时

  因此，训练 BAIL 大约比 BCQ 快35倍，比 BEAR 快 50倍

4. 结论 & 讨论

• 原文结论
  1. 对于 Training batches，BAIL 显著优于其他方法（包括BC），性能比 BCQ 提高42%，比 BC 提高101%
  2. 对于 Execution batches，BAIL 略微优于其他方法，但是不如 BC。当数据足够时，Vanilla BC 表现已经非常好了
  3. BAIL 的训练速度比其他基于 Q-function 的方法，包含 BCQ 和 BEAR 要快得多
  4. BAIL 在不同的 batch 和随机种子下表现更稳定
• 展望
  1. 将 BAIL 和探索技术相结合，得到新的 Growing-batch RL 方法
  2. 研究 BAIL 更加稳定的原因
• 我的评价
  1. 上包络网络似乎是这篇文章第一次提出的，有一定意义
  2. 本文方法 work 的一个前提，还是 batch 中数据足够多，覆盖性很好。Execution batches 中 BC 性能很好，说明 batch 中数据一定已经覆盖了大部分 $\mathcal{S}\times \mathcal{A}$ 空间，因此不会遇到严重的 mismatch 和 cascading error 问题，换句话说，如果 batch 数据少一点，或者覆盖性差一些，BAIL 这类基于 IL 方法的性能还要打问号
  3. 本文提出的 return 修正方法有局限性。对于 MuJoCo 中连续控制任务，其每个状态几乎都是等价的，而且在 MDP 这种基于马尔可夫链的，时间和状态都离散的随机过程中，如果动作空间没有任何限制，我认为任意两个 $(s,a)$ 之间都是一步可达的，因此简单地根据欧式距离拼接两端 episode 问题不大。但是对于走迷宫或者 Atari 游戏这类有一定阶段性的情况，这种简单的想法就会有问题（比如迷宫两个相邻方格间有一堵墙，那么肯定不能连接过去）